Explaining Classifiers by Constructing Familiar Concepts

Interpreting a large number of neurons in deep learning is difficult. Our proposed `CLAssifier-DECoder' architecture (ClaDec) facilitates the understanding of the output of an arbitrary layer of neurons or subsets thereof. It uses a decoder that transforms the incomprehensible representation of the given neurons to a representation that is more similar to the domain a human is familiar with. In an image recognition problem, one can recognize what information (or concepts) a layer maintains by contrasting reconstructed images of ClaDec with those of a conventional auto-encoder(AE) serving as reference. An extension of ClaDec allows trading comprehensibility and fidelity. We evaluate our approach for image classification using convolutional neural networks. We show that reconstructed visualizations using encodings from a classifier capture more relevant classification information than conventional AEs. This holds although AEs contain more information on the original input. Our user study highlights that even non-experts can identify a diverse set of concepts contained in images that are relevant (or irrelevant) for the classifier. We also compare against saliency based methods that focus on pixel relevance rather than concepts. We show that ClaDec tends to highlight more relevant input areas to classification though outcomes depend on classifier architecture. Code is at \url{https://github.com/JohnTailor/ClaDec}

Mass Personalization of Deep Learning

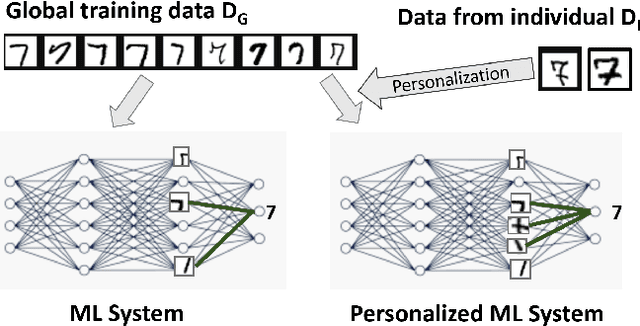
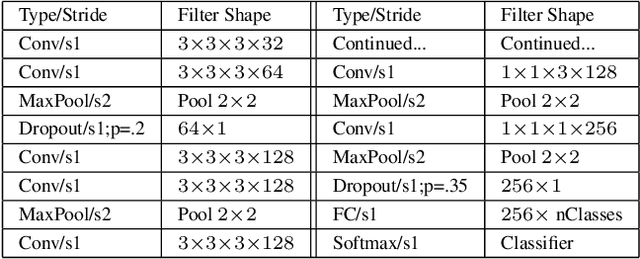
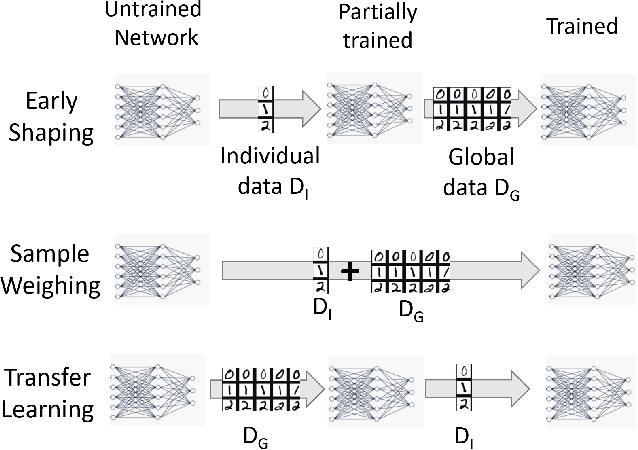
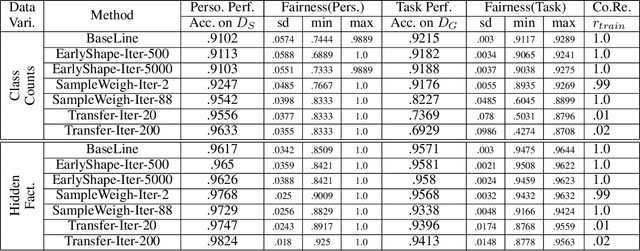
We discuss training techniques, objectives and metrics toward mass personalization of deep learning models. In machine learning, personalization refers to the fact that every trained model should be targeted towards an individual by optimizing one or several performance metrics and often obeying additional constraints. We investigate three methods for personalized training of neural networks. They constitute three forms of curriculum learning. The methods are partially inspired by the "shaping" concept from psychology. Interestingly, we discover that extensive exposure to a limited set of training data in terms of class diversity \emph{early} in the training can lead to an irreversible reduction of the capability of a network to learn from more diverse training data. This is in close alignment with existing theories in human development. In contrast, training on a small data set covering all classes \emph{early} in the training can lead to better performance.

Compressive Mining: Fast and Optimal Data Mining in the Compressed Domain

Real-world data typically contain repeated and periodic patterns. This suggests that they can be effectively represented and compressed using only a few coefficients of an appropriate basis (e.g., Fourier, Wavelets, etc.). However, distance estimation when the data are represented using different sets of coefficients is still a largely unexplored area. This work studies the optimization problems related to obtaining the \emph{tightest} lower/upper bound on Euclidean distances when each data object is potentially compressed using a different set of orthonormal coefficients. Our technique leads to tighter distance estimates, which translates into more accurate search, learning and mining operations \textit{directly} in the compressed domain. We formulate the problem of estimating lower/upper distance bounds as an optimization problem. We establish the properties of optimal solutions, and leverage the theoretical analysis to develop a fast algorithm to obtain an \emph{exact} solution to the problem. The suggested solution provides the tightest estimation of the $L_2$-norm or the correlation. We show that typical data-analysis operations, such as k-NN search or k-Means clustering, can operate more accurately using the proposed compression and distance reconstruction technique. We compare it with many other prevalent compression and reconstruction techniques, including random projections and PCA-based techniques. We highlight a surprising result, namely that when the data are highly sparse in some basis, our technique may even outperform PCA-based compression. The contributions of this work are generic as our methodology is applicable to any sequential or high-dimensional data as well as to any orthogonal data transformation used for the underlying data compression scheme.

Approximate Matrix Multiplication with Application to Linear Embeddings

In this paper, we study the problem of approximately computing the product of two real matrices. In particular, we analyze a dimensionality-reduction-based approximation algorithm due to Sarlos [1], introducing the notion of nuclear rank as the ratio of the nuclear norm over the spectral norm. The presented bound has improved dependence with respect to the approximation error (as compared to previous approaches), whereas the subspace -- on which we project the input matrices -- has dimensions proportional to the maximum of their nuclear rank and it is independent of the input dimensions. In addition, we provide an application of this result to linear low-dimensional embeddings. Namely, we show that any Euclidean point-set with bounded nuclear rank is amenable to projection onto number of dimensions that is independent of the input dimensionality, while achieving additive error guarantees.