GaNI: Global and Near Field Illumination Aware Neural Inverse Rendering

In this paper, we present GaNI, a Global and Near-field Illumination-aware neural inverse rendering technique that can reconstruct geometry, albedo, and roughness parameters from images of a scene captured with co-located light and camera. Existing inverse rendering techniques with co-located light-camera focus on single objects only, without modeling global illumination and near-field lighting more prominent in scenes with multiple objects. We introduce a system that solves this problem in two stages; we first reconstruct the geometry powered by neural volumetric rendering NeuS, followed by inverse neural radiosity that uses the previously predicted geometry to estimate albedo and roughness. However, such a naive combination fails and we propose multiple technical contributions that enable this two-stage approach. We observe that NeuS fails to handle near-field illumination and strong specular reflections from the flashlight in a scene. We propose to implicitly model the effects of near-field illumination and introduce a surface angle loss function to handle specular reflections. Similarly, we observe that invNeRad assumes constant illumination throughout the capture and cannot handle moving flashlights during capture. We propose a light position-aware radiance cache network and additional smoothness priors on roughness to reconstruct reflectance. Experimental evaluation on synthetic and real data shows that our method outperforms the existing co-located light-camera-based inverse rendering techniques. Our approach produces significantly better reflectance and slightly better geometry than capture strategies that do not require a dark room.

Inverse Global Illumination using a Neural Radiometric Prior

Inverse rendering methods that account for global illumination are becoming more popular, but current methods require evaluating and automatically differentiating millions of path integrals by tracing multiple light bounces, which remains expensive and prone to noise. Instead, this paper proposes a radiometric prior as a simple alternative to building complete path integrals in a traditional differentiable path tracer, while still correctly accounting for global illumination. Inspired by the Neural Radiosity technique, we use a neural network as a radiance function, and we introduce a prior consisting of the norm of the residual of the rendering equation in the inverse rendering loss. We train our radiance network and optimize scene parameters simultaneously using a loss consisting of both a photometric term between renderings and the multi-view input images, and our radiometric prior (the residual term). This residual term enforces a physical constraint on the optimization that ensures that the radiance field accounts for global illumination. We compare our method to a vanilla differentiable path tracer, and more advanced techniques such as Path Replay Backpropagation. Despite the simplicity of our approach, we can recover scene parameters with comparable and in some cases better quality, at considerably lower computation times.

Differentiable Neural Radiosity

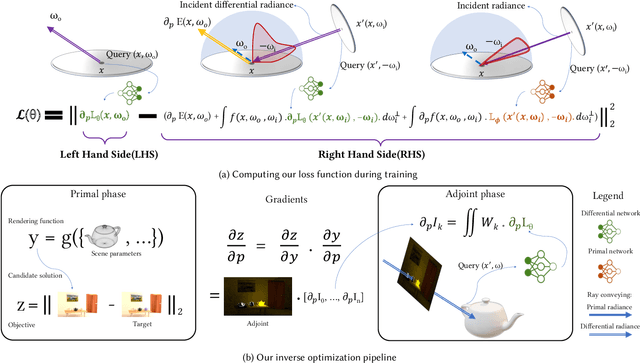
We introduce Differentiable Neural Radiosity, a novel method of representing the solution of the differential rendering equation using a neural network. Inspired by neural radiosity techniques, we minimize the norm of the residual of the differential rendering equation to directly optimize our network. The network is capable of outputting continuous, view-independent gradients of the radiance field with respect to scene parameters, taking into account differential global illumination effects while keeping memory and time complexity constant in path length. To solve inverse rendering problems, we use a pre-trained instance of our network that represents the differential radiance field with respect to a limited number of scene parameters. In our experiments, we leverage this to achieve faster and more accurate convergence compared to other techniques such as Automatic Differentiation, Radiative Backpropagation, and Path Replay Backpropagation.

Neural Radiosity

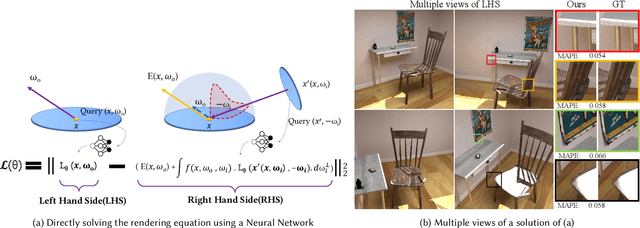
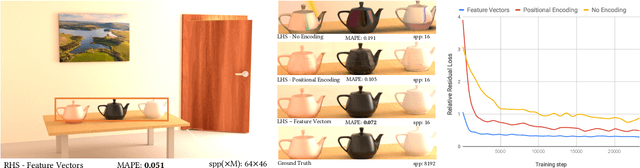
We introduce Neural Radiosity, an algorithm to solve the rendering equation by minimizing the norm of its residual similar as in traditional radiosity techniques. Traditional basis functions used in radiosity techniques, such as piecewise polynomials or meshless basis functions are typically limited to representing isotropic scattering from diffuse surfaces. Instead, we propose to leverage neural networks to represent the full four-dimensional radiance distribution, directly optimizing network parameters to minimize the norm of the residual. Our approach decouples solving the rendering equation from rendering (perspective) images similar as in traditional radiosity techniques, and allows us to efficiently synthesize arbitrary views of a scene. In addition, we propose a network architecture using geometric learnable features that improves convergence of our solver compared to previous techniques. Our approach leads to an algorithm that is simple to implement, and we demonstrate its effectiveness on a variety of scenes with non-diffuse surfaces.