Efficient Line Search Method Based on Regression and Uncertainty Quantification

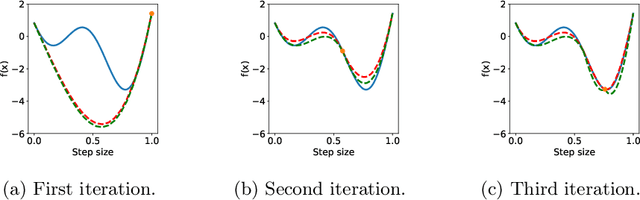
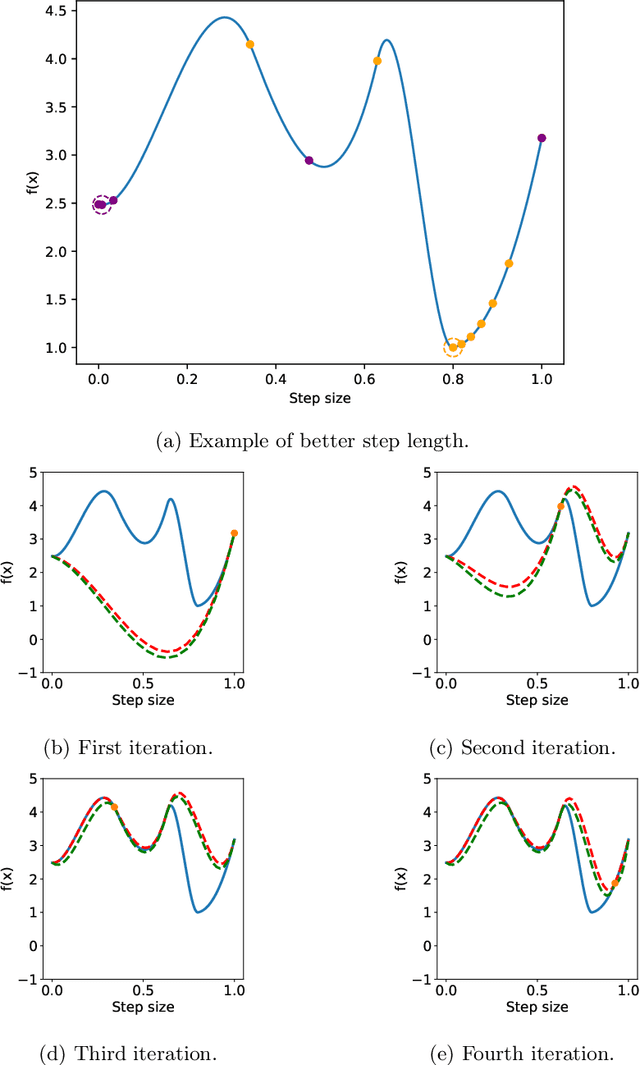
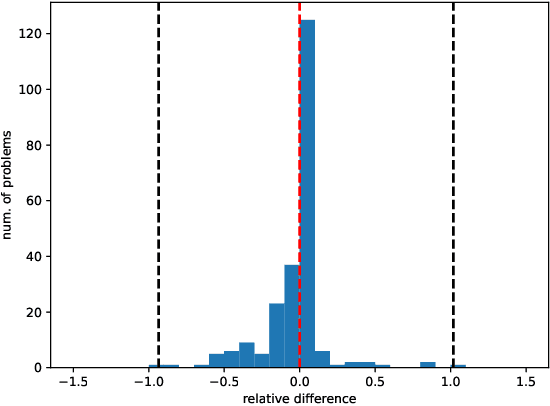
Unconstrained optimization problems are typically solved using iterative methods, which often depend on line search techniques to determine optimal step lengths in each iteration. This paper introduces a novel line search approach. Traditional line search methods, aimed at determining optimal step lengths, often discard valuable data from the search process and focus on refining step length intervals. This paper proposes a more efficient method using Bayesian optimization, which utilizes all available data points, i.e., function values and gradients, to guide the search towards a potential global minimum. This new approach more effectively explores the search space, leading to better solution quality. It is also easy to implement and integrate into existing frameworks. Tested on the challenging CUTEst test set, it demonstrates superior performance compared to existing state-of-the-art methods, solving more problems to optimality with equivalent resource usage.

Detecting Conceptual Abstraction in LLMs

We present a novel approach to detecting noun abstraction within a large language model (LLM). Starting from a psychologically motivated set of noun pairs in taxonomic relationships, we instantiate surface patterns indicating hypernymy and analyze the attention matrices produced by BERT. We compare the results to two sets of counterfactuals and show that we can detect hypernymy in the abstraction mechanism, which cannot solely be related to the distributional similarity of noun pairs. Our findings are a first step towards the explainability of conceptual abstraction in LLMs.

Why Capsule Neural Networks Do Not Scale: Challenging the Dynamic Parse-Tree Assumption

Capsule neural networks replace simple, scalar-valued neurons with vector-valued capsules. They are motivated by the pattern recognition system in the human brain, where complex objects are decomposed into a hierarchy of simpler object parts. Such a hierarchy is referred to as a parse-tree. Conceptually, capsule neural networks have been defined to realize such parse-trees. The capsule neural network (CapsNet), by Sabour, Frosst, and Hinton, is the first actual implementation of the conceptual idea of capsule neural networks. CapsNets achieved state-of-the-art performance on simple image recognition tasks with fewer parameters and greater robustness to affine transformations than comparable approaches. This sparked extensive follow-up research. However, despite major efforts, no work was able to scale the CapsNet architecture to more reasonable-sized datasets. Here, we provide a reason for this failure and argue that it is most likely not possible to scale CapsNets beyond toy examples. In particular, we show that the concept of a parse-tree, the main idea behind capsule neuronal networks, is not present in CapsNets. We also show theoretically and experimentally that CapsNets suffer from a vanishing gradient problem that results in the starvation of many capsules during training.

Convexity Certificates from Hessians

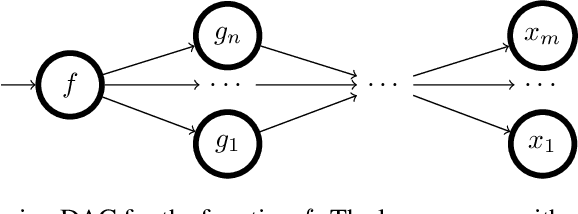
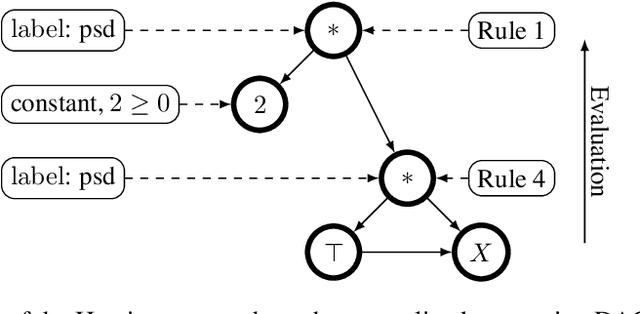
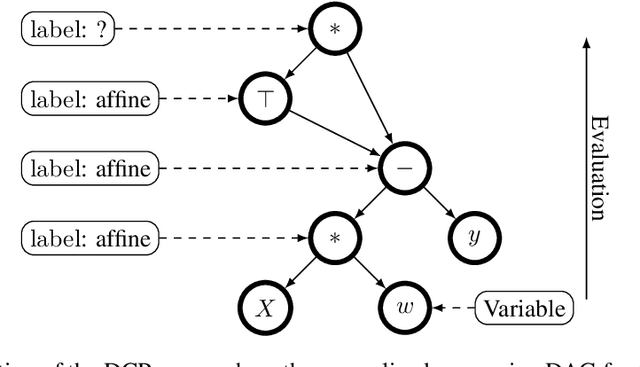
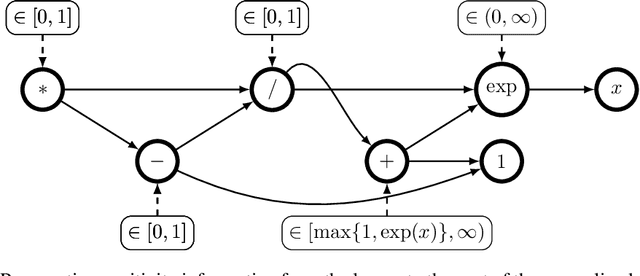
The Hessian of a differentiable convex function is positive semidefinite. Therefore, checking the Hessian of a given function is a natural approach to certify convexity. However, implementing this approach is not straightforward since it requires a representation of the Hessian that allows its analysis. Here, we implement this approach for a class of functions that is rich enough to support classical machine learning. For this class of functions, it was recently shown how to compute computational graphs of their Hessians. We show how to check these graphs for positive semidefiniteness. We compare our implementation of the Hessian approach with the well-established disciplined convex programming (DCP) approach and prove that the Hessian approach is at least as powerful as the DCP approach for differentiable functions. Furthermore, we show for a state-of-the-art implementation of the DCP approach that, for differentiable functions, the Hessian approach is actually more powerful. That is, it can certify the convexity of a larger class of differentiable functions.

Optimization for Classical Machine Learning Problems on the GPU

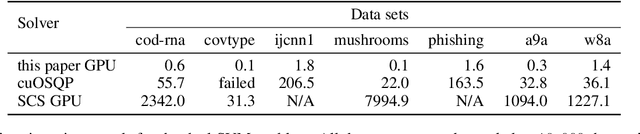
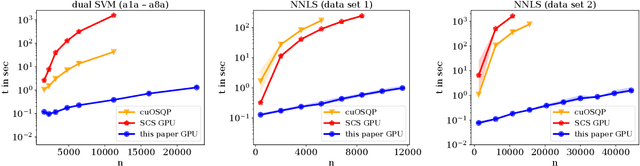
Constrained optimization problems arise frequently in classical machine learning. There exist frameworks addressing constrained optimization, for instance, CVXPY and GENO. However, in contrast to deep learning frameworks, GPU support is limited. Here, we extend the GENO framework to also solve constrained optimization problems on the GPU. The framework allows the user to specify constrained optimization problems in an easy-to-read modeling language. A solver is then automatically generated from this specification. When run on the GPU, the solver outperforms state-of-the-art approaches like CVXPY combined with a GPU-accelerated solver such as cuOSQP or SCS by a few orders of magnitude.

A Simple and Efficient Tensor Calculus for Machine Learning

Computing derivatives of tensor expressions, also known as tensor calculus, is a fundamental task in machine learning. A key concern is the efficiency of evaluating the expressions and their derivatives that hinges on the representation of these expressions. Recently, an algorithm for computing higher order derivatives of tensor expressions like Jacobians or Hessians has been introduced that is a few orders of magnitude faster than previous state-of-the-art approaches. Unfortunately, the approach is based on Ricci notation and hence cannot be incorporated into automatic differentiation frameworks from deep learning like TensorFlow, PyTorch, autograd, or JAX that use the simpler Einstein notation. This leaves two options, to either change the underlying tensor representation in these frameworks or to develop a new, provably correct algorithm based on Einstein notation. Obviously, the first option is impractical. Hence, we pursue the second option. Here, we show that using Ricci notation is not necessary for an efficient tensor calculus and develop an equally efficient method for the simpler Einstein notation. It turns out that turning to Einstein notation enables further improvements that lead to even better efficiency. The methods that are described in this paper have been implemented in the online tool www.MatrixCalculus.org for computing derivatives of matrix and tensor expressions. An extended abstract of this paper appeared as "A Simple and Efficient Tensor Calculus", AAAI 2020.

GENO -- GENeric Optimization for Classical Machine Learning

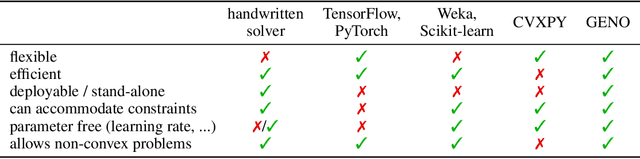
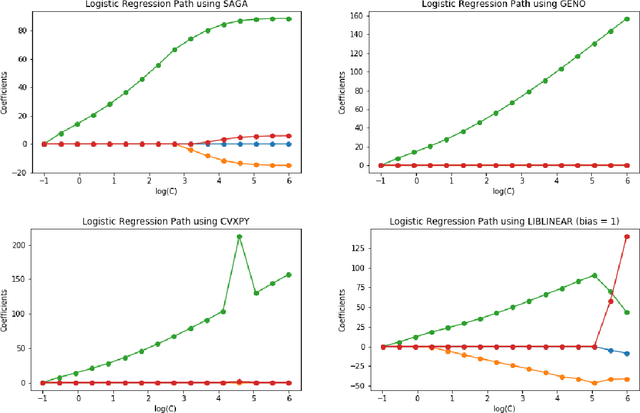
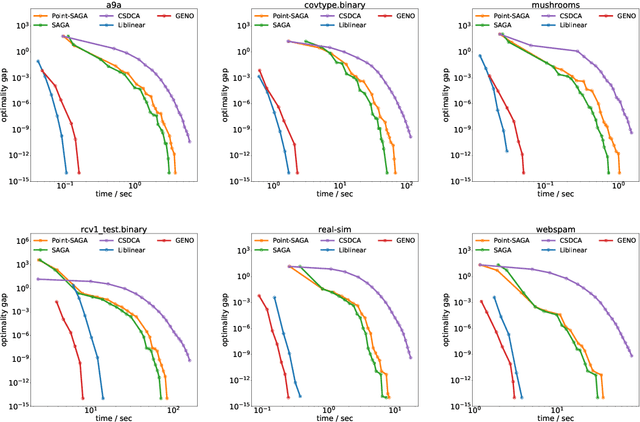
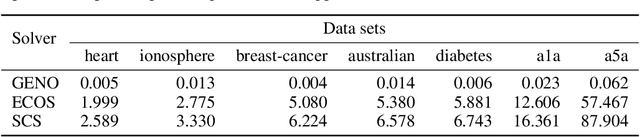
Although optimization is the longstanding algorithmic backbone of machine learning, new models still require the time-consuming implementation of new solvers. As a result, there are thousands of implementations of optimization algorithms for machine learning problems. A natural question is, if it is always necessary to implement a new solver, or if there is one algorithm that is sufficient for most models. Common belief suggests that such a one-algorithm-fits-all approach cannot work, because this algorithm cannot exploit model specific structure and thus cannot be efficient and robust on a wide variety of problems. Here, we challenge this common belief. We have designed and implemented the optimization framework GENO (GENeric Optimization) that combines a modeling language with a generic solver. GENO generates a solver from the declarative specification of an optimization problem class. The framework is flexible enough to encompass most of the classical machine learning problems. We show on a wide variety of classical but also some recently suggested problems that the automatically generated solvers are (1) as efficient as well-engineered specialized solvers, (2) more efficient by a decent margin than recent state-of-the-art solvers, and (3) orders of magnitude more efficient than classical modeling language plus solver approaches.

Distributed Convex Optimization with Many Convex Constraints

We address the problem of solving convex optimization problems with many convex constraints in a distributed setting. Our approach is based on an extension of the alternating direction method of multipliers (ADMM) that recently gained a lot of attention in the Big Data context. Although it has been invented decades ago, ADMM so far can be applied only to unconstrained problems and problems with linear equality or inequality constraints. Our extension can handle arbitrary inequality constraints directly. It combines the ability of ADMM to solve convex optimization problems in a distributed setting with the ability of the Augmented Lagrangian method to solve constrained optimization problems, and as we show, it inherits the convergence guarantees of ADMM and the Augmented Lagrangian method.