Why Capsule Neural Networks Do Not Scale: Challenging the Dynamic Parse-Tree Assumption

Capsule neural networks replace simple, scalar-valued neurons with vector-valued capsules. They are motivated by the pattern recognition system in the human brain, where complex objects are decomposed into a hierarchy of simpler object parts. Such a hierarchy is referred to as a parse-tree. Conceptually, capsule neural networks have been defined to realize such parse-trees. The capsule neural network (CapsNet), by Sabour, Frosst, and Hinton, is the first actual implementation of the conceptual idea of capsule neural networks. CapsNets achieved state-of-the-art performance on simple image recognition tasks with fewer parameters and greater robustness to affine transformations than comparable approaches. This sparked extensive follow-up research. However, despite major efforts, no work was able to scale the CapsNet architecture to more reasonable-sized datasets. Here, we provide a reason for this failure and argue that it is most likely not possible to scale CapsNets beyond toy examples. In particular, we show that the concept of a parse-tree, the main idea behind capsule neuronal networks, is not present in CapsNets. We also show theoretically and experimentally that CapsNets suffer from a vanishing gradient problem that results in the starvation of many capsules during training.

A Simple and Efficient Tensor Calculus for Machine Learning

Computing derivatives of tensor expressions, also known as tensor calculus, is a fundamental task in machine learning. A key concern is the efficiency of evaluating the expressions and their derivatives that hinges on the representation of these expressions. Recently, an algorithm for computing higher order derivatives of tensor expressions like Jacobians or Hessians has been introduced that is a few orders of magnitude faster than previous state-of-the-art approaches. Unfortunately, the approach is based on Ricci notation and hence cannot be incorporated into automatic differentiation frameworks from deep learning like TensorFlow, PyTorch, autograd, or JAX that use the simpler Einstein notation. This leaves two options, to either change the underlying tensor representation in these frameworks or to develop a new, provably correct algorithm based on Einstein notation. Obviously, the first option is impractical. Hence, we pursue the second option. Here, we show that using Ricci notation is not necessary for an efficient tensor calculus and develop an equally efficient method for the simpler Einstein notation. It turns out that turning to Einstein notation enables further improvements that lead to even better efficiency. The methods that are described in this paper have been implemented in the online tool www.MatrixCalculus.org for computing derivatives of matrix and tensor expressions. An extended abstract of this paper appeared as "A Simple and Efficient Tensor Calculus", AAAI 2020.

GENO -- GENeric Optimization for Classical Machine Learning

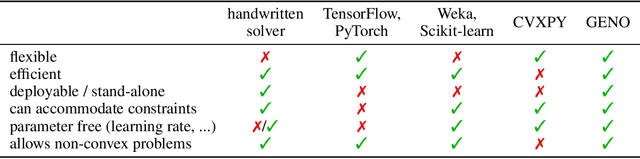
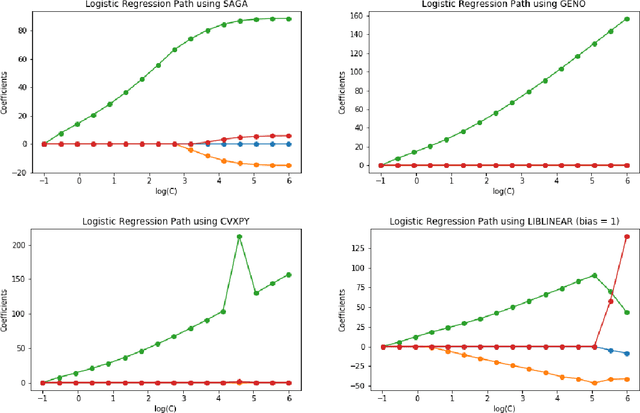
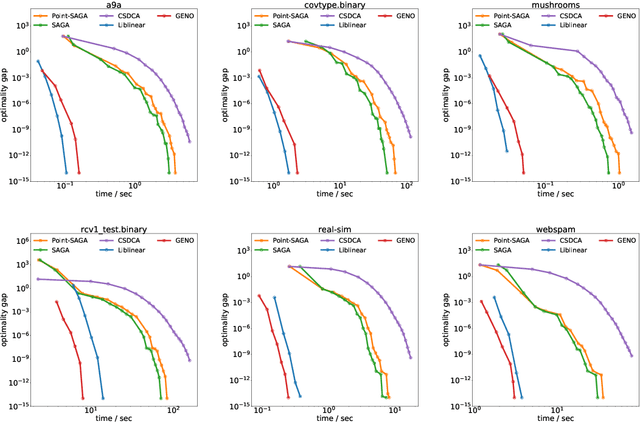
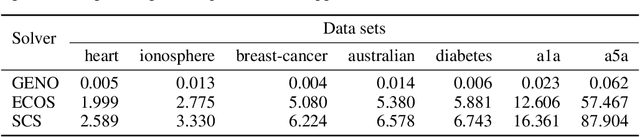
Although optimization is the longstanding algorithmic backbone of machine learning, new models still require the time-consuming implementation of new solvers. As a result, there are thousands of implementations of optimization algorithms for machine learning problems. A natural question is, if it is always necessary to implement a new solver, or if there is one algorithm that is sufficient for most models. Common belief suggests that such a one-algorithm-fits-all approach cannot work, because this algorithm cannot exploit model specific structure and thus cannot be efficient and robust on a wide variety of problems. Here, we challenge this common belief. We have designed and implemented the optimization framework GENO (GENeric Optimization) that combines a modeling language with a generic solver. GENO generates a solver from the declarative specification of an optimization problem class. The framework is flexible enough to encompass most of the classical machine learning problems. We show on a wide variety of classical but also some recently suggested problems that the automatically generated solvers are (1) as efficient as well-engineered specialized solvers, (2) more efficient by a decent margin than recent state-of-the-art solvers, and (3) orders of magnitude more efficient than classical modeling language plus solver approaches.