Discovering Symmetries of ODEs by Symbolic Regression

Solving systems of ordinary differential equations (ODEs) is essential when it comes to understanding the behavior of dynamical systems. Yet, automated solving remains challenging, in particular for nonlinear systems. Computer algebra systems (CASs) provide support for solving ODEs by first simplifying them, in particular through the use of Lie point symmetries. Finding these symmetries is, however, itself a difficult problem for CASs. Recent works in symbolic regression have shown promising results for recovering symbolic expressions from data. Here, we adapt search-based symbolic regression to the task of finding generators of Lie point symmetries. With this approach, we can find symmetries of ODEs that existing CASs cannot find.

Scaling Up Unbiased Search-based Symbolic Regression

In a regression task, a function is learned from labeled data to predict the labels at new data points. The goal is to achieve small prediction errors. In symbolic regression, the goal is more ambitious, namely, to learn an interpretable function that makes small prediction errors. This additional goal largely rules out the standard approach used in regression, that is, reducing the learning problem to learning parameters of an expansion of basis functions by optimization. Instead, symbolic regression methods search for a good solution in a space of symbolic expressions. To cope with the typically vast search space, most symbolic regression methods make implicit, or sometimes even explicit, assumptions about its structure. Here, we argue that the only obvious structure of the search space is that it contains small expressions, that is, expressions that can be decomposed into a few subexpressions. We show that systematically searching spaces of small expressions finds solutions that are more accurate and more robust against noise than those obtained by state-of-the-art symbolic regression methods. In particular, systematic search outperforms state-of-the-art symbolic regressors in terms of its ability to recover the true underlying symbolic expressions on established benchmark data sets.

Dimension Reduction for Symbolic Regression

Solutions of symbolic regression problems are expressions that are composed of input variables and operators from a finite set of function symbols. One measure for evaluating symbolic regression algorithms is their ability to recover formulae, up to symbolic equivalence, from finite samples. Not unexpectedly, the recovery problem becomes harder when the formula gets more complex, that is, when the number of variables and operators gets larger. Variables in naturally occurring symbolic formulas often appear only in fixed combinations. This can be exploited in symbolic regression by substituting one new variable for the combination, effectively reducing the number of variables. However, finding valid substitutions is challenging. Here, we address this challenge by searching over the expression space of small substitutions and testing for validity. The validity test is reduced to a test of functional dependence. The resulting iterative dimension reduction procedure can be used with any symbolic regression approach. We show that it reliably identifies valid substitutions and significantly boosts the performance of different types of state-of-the-art symbolic regression algorithms.

Why Capsule Neural Networks Do Not Scale: Challenging the Dynamic Parse-Tree Assumption

Capsule neural networks replace simple, scalar-valued neurons with vector-valued capsules. They are motivated by the pattern recognition system in the human brain, where complex objects are decomposed into a hierarchy of simpler object parts. Such a hierarchy is referred to as a parse-tree. Conceptually, capsule neural networks have been defined to realize such parse-trees. The capsule neural network (CapsNet), by Sabour, Frosst, and Hinton, is the first actual implementation of the conceptual idea of capsule neural networks. CapsNets achieved state-of-the-art performance on simple image recognition tasks with fewer parameters and greater robustness to affine transformations than comparable approaches. This sparked extensive follow-up research. However, despite major efforts, no work was able to scale the CapsNet architecture to more reasonable-sized datasets. Here, we provide a reason for this failure and argue that it is most likely not possible to scale CapsNets beyond toy examples. In particular, we show that the concept of a parse-tree, the main idea behind capsule neuronal networks, is not present in CapsNets. We also show theoretically and experimentally that CapsNets suffer from a vanishing gradient problem that results in the starvation of many capsules during training.

Convexity Certificates from Hessians

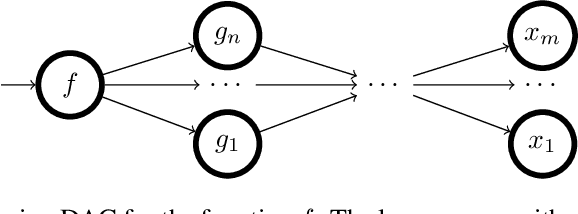
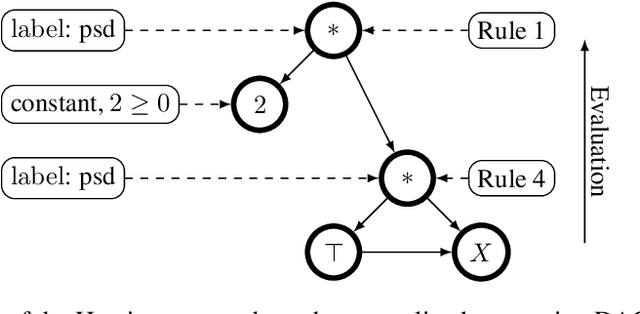
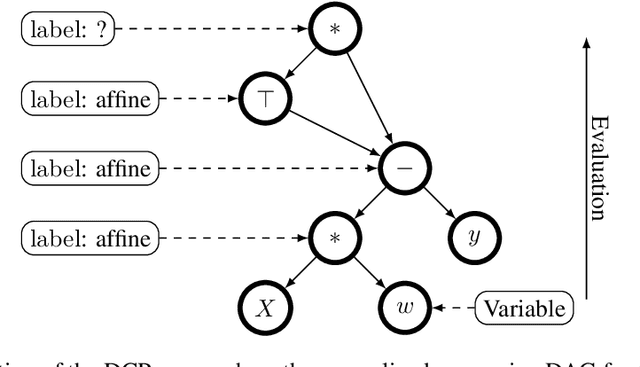
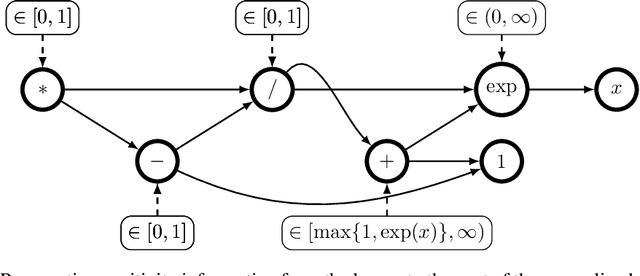
The Hessian of a differentiable convex function is positive semidefinite. Therefore, checking the Hessian of a given function is a natural approach to certify convexity. However, implementing this approach is not straightforward since it requires a representation of the Hessian that allows its analysis. Here, we implement this approach for a class of functions that is rich enough to support classical machine learning. For this class of functions, it was recently shown how to compute computational graphs of their Hessians. We show how to check these graphs for positive semidefiniteness. We compare our implementation of the Hessian approach with the well-established disciplined convex programming (DCP) approach and prove that the Hessian approach is at least as powerful as the DCP approach for differentiable functions. Furthermore, we show for a state-of-the-art implementation of the DCP approach that, for differentiable functions, the Hessian approach is actually more powerful. That is, it can certify the convexity of a larger class of differentiable functions.

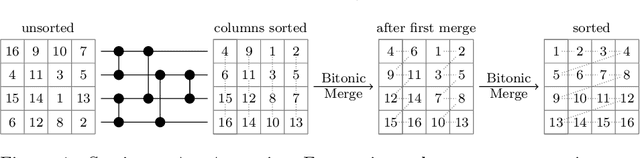
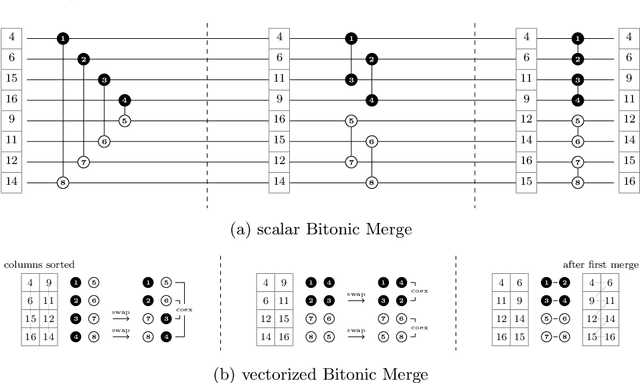
Vectorized and performance-portable Quicksort

Recent works showed that implementations of Quicksort using vector CPU instructions can outperform the non-vectorized algorithms in widespread use. However, these implementations are typically single-threaded, implemented for a particular instruction set, and restricted to a small set of key types. We lift these three restrictions: our proposed 'vqsort' algorithm integrates into the state-of-the-art parallel sorter 'ips4o', with a geometric mean speedup of 1.59. The same implementation works on seven instruction sets (including SVE and RISC-V V) across four platforms. It also supports floating-point and 16-128 bit integer keys. To the best of our knowledge, this is the fastest sort for non-tuple keys on CPUs, up to 20 times as fast as the sorting algorithms implemented in standard libraries. This paper focuses on the practical engineering aspects enabling the speed and portability, which we have not yet seen demonstrated for a Quicksort implementation. Furthermore, we introduce compact and transpose-free sorting networks for in-register sorting of small arrays, and a vector-friendly pivot sampling strategy that is robust against adversarial input.

Optimization for Classical Machine Learning Problems on the GPU

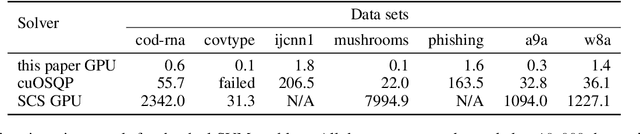
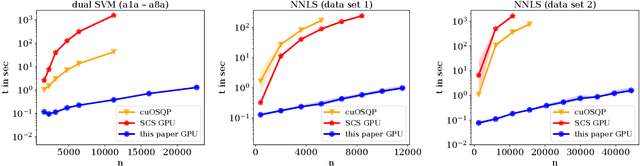
Constrained optimization problems arise frequently in classical machine learning. There exist frameworks addressing constrained optimization, for instance, CVXPY and GENO. However, in contrast to deep learning frameworks, GPU support is limited. Here, we extend the GENO framework to also solve constrained optimization problems on the GPU. The framework allows the user to specify constrained optimization problems in an easy-to-read modeling language. A solver is then automatically generated from this specification. When run on the GPU, the solver outperforms state-of-the-art approaches like CVXPY combined with a GPU-accelerated solver such as cuOSQP or SCS by a few orders of magnitude.

A Simple and Efficient Tensor Calculus for Machine Learning

Computing derivatives of tensor expressions, also known as tensor calculus, is a fundamental task in machine learning. A key concern is the efficiency of evaluating the expressions and their derivatives that hinges on the representation of these expressions. Recently, an algorithm for computing higher order derivatives of tensor expressions like Jacobians or Hessians has been introduced that is a few orders of magnitude faster than previous state-of-the-art approaches. Unfortunately, the approach is based on Ricci notation and hence cannot be incorporated into automatic differentiation frameworks from deep learning like TensorFlow, PyTorch, autograd, or JAX that use the simpler Einstein notation. This leaves two options, to either change the underlying tensor representation in these frameworks or to develop a new, provably correct algorithm based on Einstein notation. Obviously, the first option is impractical. Hence, we pursue the second option. Here, we show that using Ricci notation is not necessary for an efficient tensor calculus and develop an equally efficient method for the simpler Einstein notation. It turns out that turning to Einstein notation enables further improvements that lead to even better efficiency. The methods that are described in this paper have been implemented in the online tool www.MatrixCalculus.org for computing derivatives of matrix and tensor expressions. An extended abstract of this paper appeared as "A Simple and Efficient Tensor Calculus", AAAI 2020.

GENO -- GENeric Optimization for Classical Machine Learning

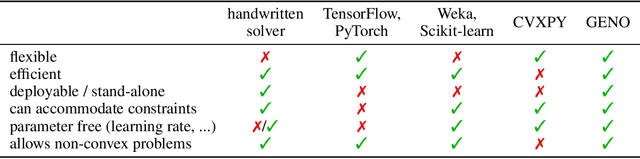
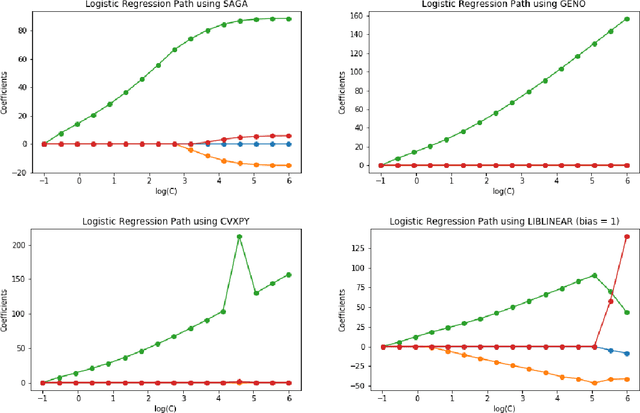
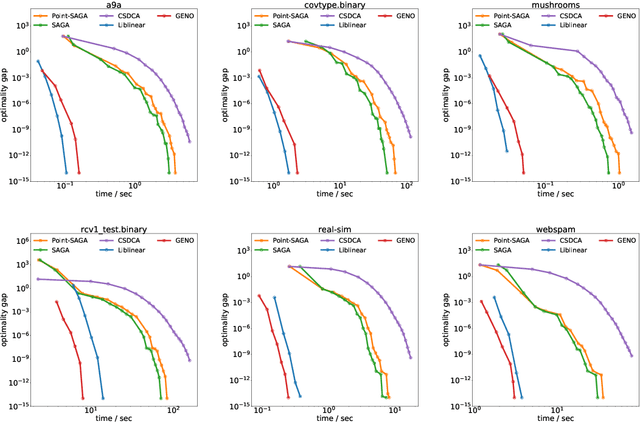
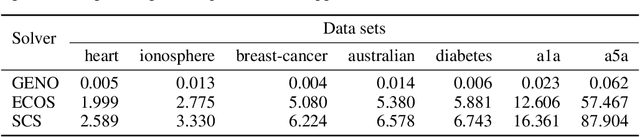
Although optimization is the longstanding algorithmic backbone of machine learning, new models still require the time-consuming implementation of new solvers. As a result, there are thousands of implementations of optimization algorithms for machine learning problems. A natural question is, if it is always necessary to implement a new solver, or if there is one algorithm that is sufficient for most models. Common belief suggests that such a one-algorithm-fits-all approach cannot work, because this algorithm cannot exploit model specific structure and thus cannot be efficient and robust on a wide variety of problems. Here, we challenge this common belief. We have designed and implemented the optimization framework GENO (GENeric Optimization) that combines a modeling language with a generic solver. GENO generates a solver from the declarative specification of an optimization problem class. The framework is flexible enough to encompass most of the classical machine learning problems. We show on a wide variety of classical but also some recently suggested problems that the automatically generated solvers are (1) as efficient as well-engineered specialized solvers, (2) more efficient by a decent margin than recent state-of-the-art solvers, and (3) orders of magnitude more efficient than classical modeling language plus solver approaches.

Ising Models with Latent Conditional Gaussian Variables

Ising models describe the joint probability distribution of a vector of binary feature variables. Typically, not all the variables interact with each other and one is interested in learning the presumably sparse network structure of the interacting variables. However, in the presence of latent variables, the conventional method of learning a sparse model might fail. This is because the latent variables induce indirect interactions of the observed variables. In the case of only a few latent conditional Gaussian variables these spurious interactions contribute an additional low-rank component to the interaction parameters of the observed Ising model. Therefore, we propose to learn a sparse + low-rank decomposition of the parameters of an Ising model using a convex regularized likelihood problem. We show that the same problem can be obtained as the dual of a maximum-entropy problem with a new type of relaxation, where the sample means collectively need to match the expected values only up to a given tolerance. The solution to the convex optimization problem has consistency properties in the high-dimensional setting, where the number of observed binary variables and the number of latent conditional Gaussian variables are allowed to grow with the number of training samples.