Pushing the Limits: Concurrency Detection in Acyclic, Live, and 1-Safe Free-Choice Nets in $O\big((P + T)^2\big)$

Concurrency is an important aspect of (Petri) nets to describe and simulate the behavior of complex systems. Knowing which places and transitions could be executed in parallel helps to understand nets and enables analysis techniques and the computation of other properties, such as causality, exclusivity, etc.. All techniques based on concurrency detection depend on the efficiency of this detection methodology. Kovalyov and Esparza have developed algorithms that compute all concurrent places in $O\big((P+T)TP^2\big)$ for live nets (where $P$ and $T$ are the numbers of places and transitions) and in $O\big(P(P+T)^2\big)$ for live free-choice nets. Although these algorithms have a reasonably good computational complexity, large numbers of concurrent pairs of nodes may still lead to long computation times. Furthermore, both algorithms cannot be parallelized without additional effort. This paper complements the palette of concurrency detection algorithms with the Concurrent Paths (CP) algorithm for safe, live, free-choice nets. The algorithm allows parallelization and has a worst-case computational complexity of $O\big((P+T)^2\big)$ for acyclic nets and of $O\big(P^3+PT^2\big)$ for cyclic nets. Although the computational complexity of cyclic nets has not improved, the evaluation shows the benefits of CP, especially, if the net contains many nodes in concurrency relation.

Convexity Certificates from Hessians

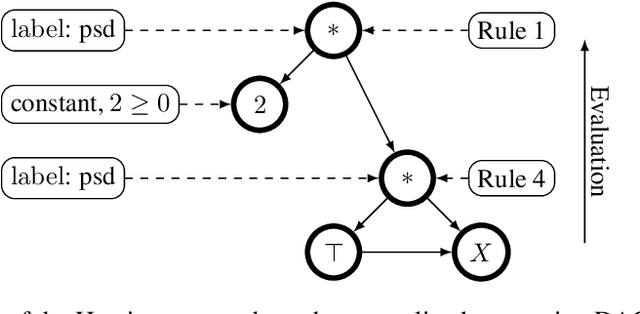
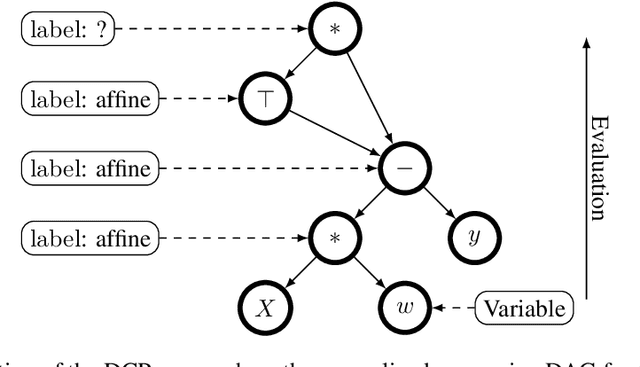
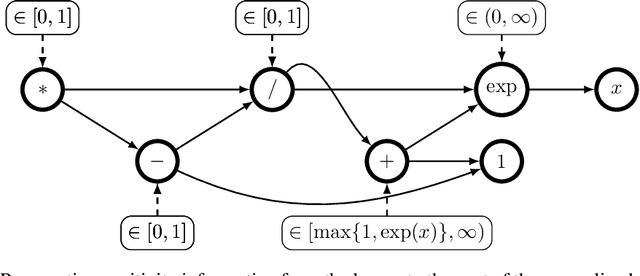
The Hessian of a differentiable convex function is positive semidefinite. Therefore, checking the Hessian of a given function is a natural approach to certify convexity. However, implementing this approach is not straightforward since it requires a representation of the Hessian that allows its analysis. Here, we implement this approach for a class of functions that is rich enough to support classical machine learning. For this class of functions, it was recently shown how to compute computational graphs of their Hessians. We show how to check these graphs for positive semidefiniteness. We compare our implementation of the Hessian approach with the well-established disciplined convex programming (DCP) approach and prove that the Hessian approach is at least as powerful as the DCP approach for differentiable functions. Furthermore, we show for a state-of-the-art implementation of the DCP approach that, for differentiable functions, the Hessian approach is actually more powerful. That is, it can certify the convexity of a larger class of differentiable functions.