Efficient Line Search Method Based on Regression and Uncertainty Quantification
Paper and Code
May 17, 2024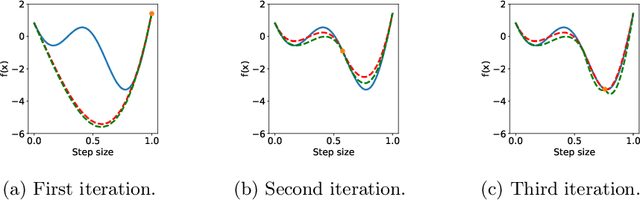

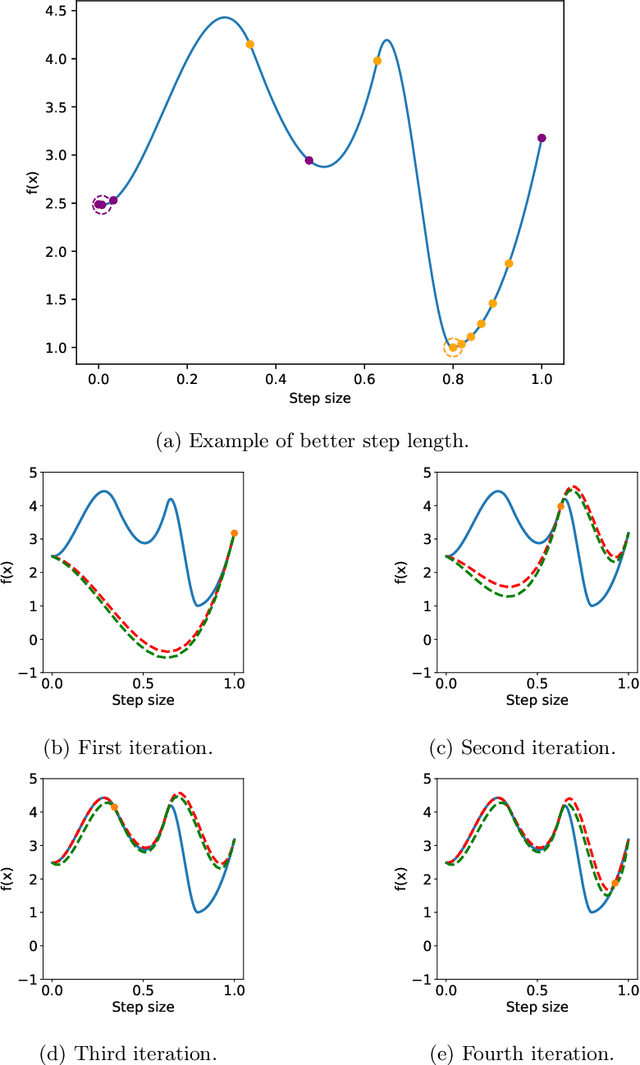
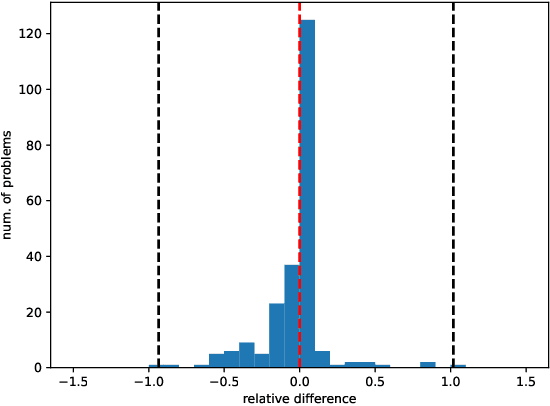
Unconstrained optimization problems are typically solved using iterative methods, which often depend on line search techniques to determine optimal step lengths in each iteration. This paper introduces a novel line search approach. Traditional line search methods, aimed at determining optimal step lengths, often discard valuable data from the search process and focus on refining step length intervals. This paper proposes a more efficient method using Bayesian optimization, which utilizes all available data points, i.e., function values and gradients, to guide the search towards a potential global minimum. This new approach more effectively explores the search space, leading to better solution quality. It is also easy to implement and integrate into existing frameworks. Tested on the challenging CUTEst test set, it demonstrates superior performance compared to existing state-of-the-art methods, solving more problems to optimality with equivalent resource usage.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge