Uncovering the Limitations of Query Performance Prediction: Failures, Insights, and Implications for Selective Query Processing

Query Performance Prediction (QPP) estimates retrieval systems effectiveness for a given query, offering valuable insights for search effectiveness and query processing. Despite extensive research, QPPs face critical challenges in generalizing across diverse retrieval paradigms and collections. This paper provides a comprehensive evaluation of state-of-the-art QPPs (e.g. NQC, UQC), LETOR-based features, and newly explored dense-based predictors. Using diverse sparse rankers (BM25, DFree without and with query expansion) and hybrid or dense (SPLADE and ColBert) rankers and diverse test collections ROBUST, GOV2, WT10G, and MS MARCO; we investigate the relationships between predicted and actual performance, with a focus on generalization and robustness. Results show significant variability in predictors accuracy, with collections as the main factor and rankers next. Some sparse predictors perform somehow on some collections (TREC ROBUST and GOV2) but do not generalise to other collections (WT10G and MS-MARCO). While some predictors show promise in specific scenarios, their overall limitations constrain their utility for applications. We show that QPP-driven selective query processing offers only marginal gains, emphasizing the need for improved predictors that generalize across collections, align with dense retrieval architectures and are useful for downstream applications.

Forward and Backward Feature Selection for Query Performance Prediction

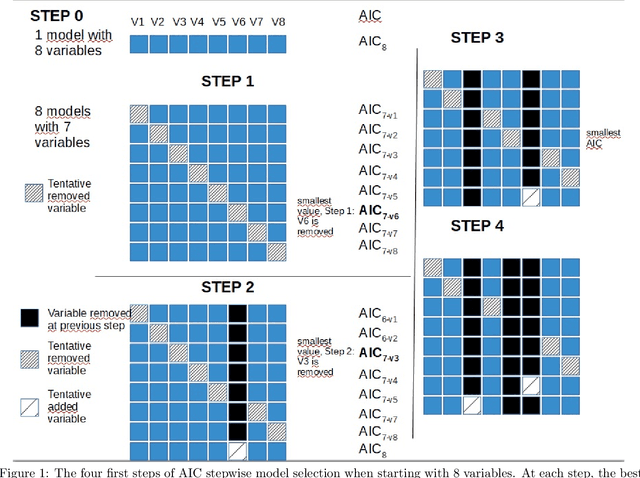
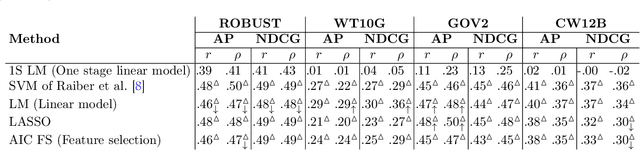
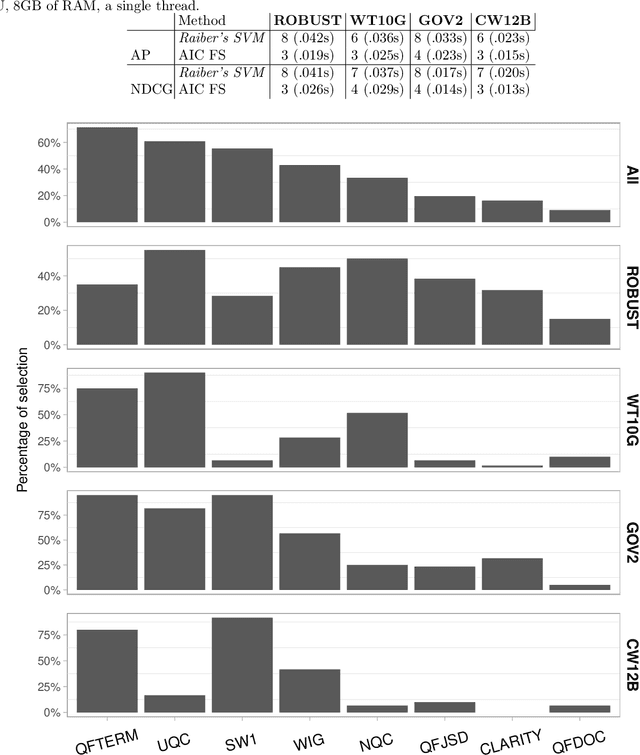
The goal of query performance prediction (QPP) is to automatically estimate the effectiveness of a search result for any given query, without relevance judgements. Post-retrieval features have been shown to be more effective for this task while being more expensive to compute than pre-retrieval features. Combining multiple post-retrieval features is even more effective, but state-of-the-art QPP methods are impossible to interpret because of the black-box nature of the employed machine learning models. However, interpretation is useful for understanding the predictive model and providing more answers about its behavior. Moreover, combining many post-retrieval features is not applicable to real-world cases, since the query running time is of utter importance. In this paper, we investigate a new framework for feature selection in which the trained model explains well the prediction. We introduce a step-wise (forward and backward) model selection approach where different subsets of query features are used to fit different models from which the system selects the best one. We evaluate our approach on four TREC collections using standard QPP features. We also develop two QPP features to address the issue of query-drift in the query feedback setting. We found that: (1) our model based on a limited number of selected features is as good as more complex models for QPP and better than non-selective models; (2) our model is more efficient than complex models during inference time since it requires fewer features; (3) the predictive model is readable and understandable; and (4) one of our new QPP features is consistently selected across different collections, proving its usefulness.

Non-convex Regularizations for Feature Selection in Ranking With Sparse SVM

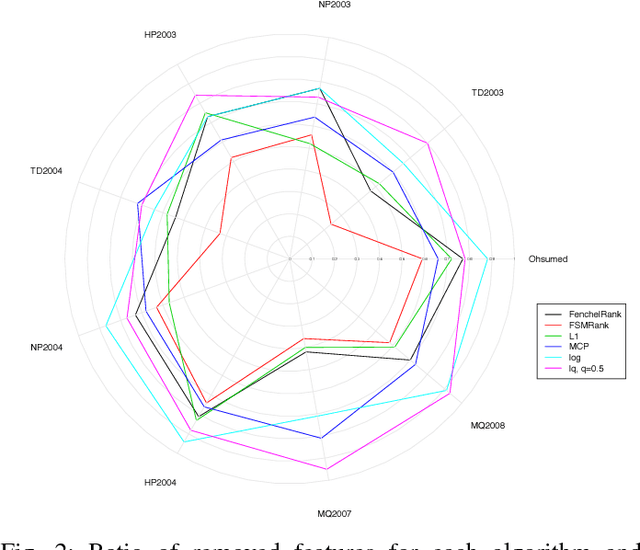
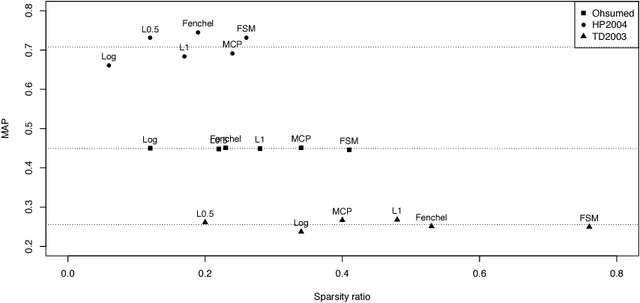
Feature selection in learning to rank has recently emerged as a crucial issue. Whereas several preprocessing approaches have been proposed, only a few works have been focused on integrating the feature selection into the learning process. In this work, we propose a general framework for feature selection in learning to rank using SVM with a sparse regularization term. We investigate both classical convex regularizations such as $\ell\_1$ or weighted $\ell\_1$ and non-convex regularization terms such as log penalty, Minimax Concave Penalty (MCP) or $\ell\_p$ pseudo norm with $p\textless{}1$. Two algorithms are proposed, first an accelerated proximal approach for solving the convex problems, second a reweighted $\ell\_1$ scheme to address the non-convex regularizations. We conduct intensive experiments on nine datasets from Letor 3.0 and Letor 4.0 corpora. Numerical results show that the use of non-convex regularizations we propose leads to more sparsity in the resulting models while prediction performance is preserved. The number of features is decreased by up to a factor of six compared to the $\ell\_1$ regularization. In addition, the software is publicly available on the web.