Non-convex Regularizations for Feature Selection in Ranking With Sparse SVM
Paper and Code
Jul 02, 2015
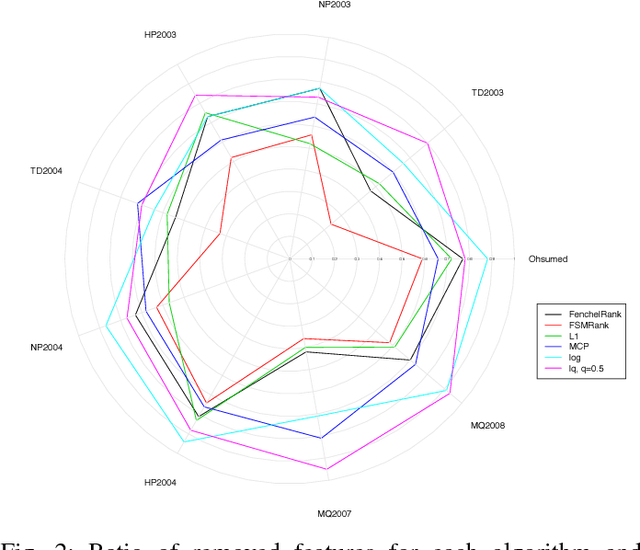
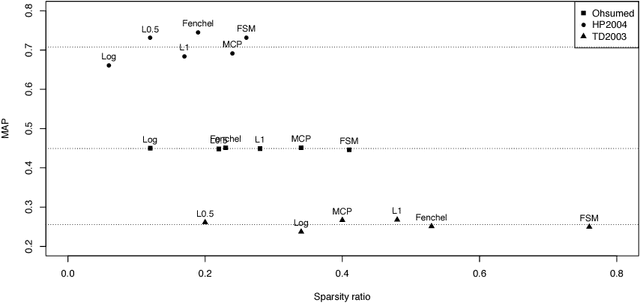

Feature selection in learning to rank has recently emerged as a crucial issue. Whereas several preprocessing approaches have been proposed, only a few works have been focused on integrating the feature selection into the learning process. In this work, we propose a general framework for feature selection in learning to rank using SVM with a sparse regularization term. We investigate both classical convex regularizations such as $\ell\_1$ or weighted $\ell\_1$ and non-convex regularization terms such as log penalty, Minimax Concave Penalty (MCP) or $\ell\_p$ pseudo norm with $p\textless{}1$. Two algorithms are proposed, first an accelerated proximal approach for solving the convex problems, second a reweighted $\ell\_1$ scheme to address the non-convex regularizations. We conduct intensive experiments on nine datasets from Letor 3.0 and Letor 4.0 corpora. Numerical results show that the use of non-convex regularizations we propose leads to more sparsity in the resulting models while prediction performance is preserved. The number of features is decreased by up to a factor of six compared to the $\ell\_1$ regularization. In addition, the software is publicly available on the web.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge