Exploring Effects of Hyperdimensional Vectors for Tsetlin Machines

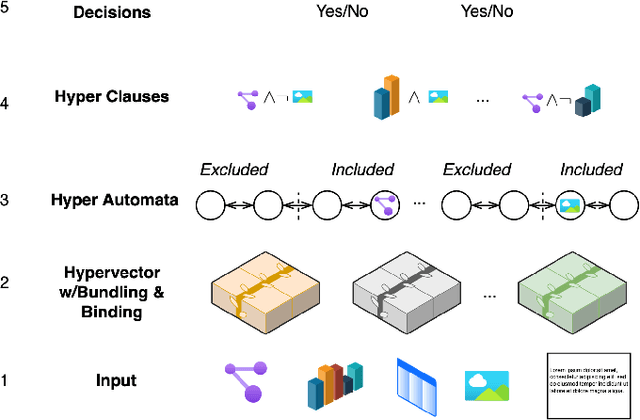
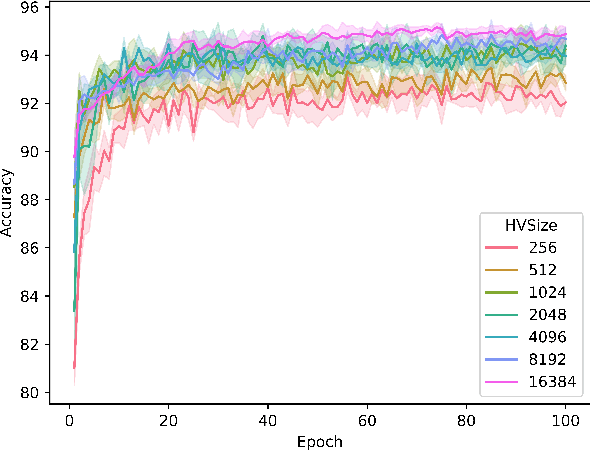
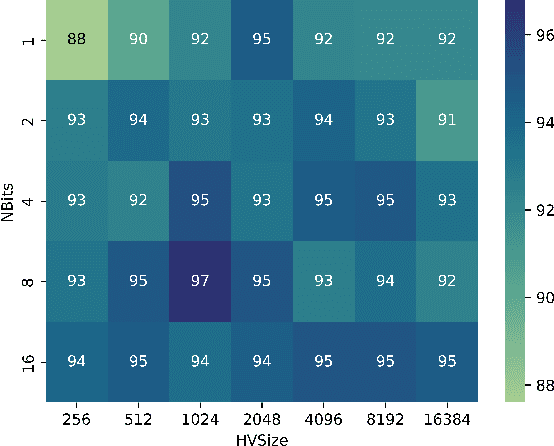
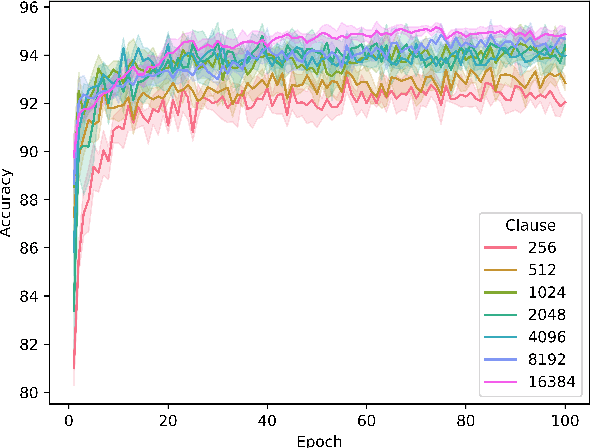
Tsetlin machines (TMs) have been successful in several application domains, operating with high efficiency on Boolean representations of the input data. However, Booleanizing complex data structures such as sequences, graphs, images, signal spectra, chemical compounds, and natural language is not trivial. In this paper, we propose a hypervector (HV) based method for expressing arbitrarily large sets of concepts associated with any input data. Using a hyperdimensional space to build vectors drastically expands the capacity and flexibility of the TM. We demonstrate how images, chemical compounds, and natural language text are encoded according to the proposed method, and how the resulting HV-powered TM can achieve significantly higher accuracy and faster learning on well-known benchmarks. Our results open up a new research direction for TMs, namely how to expand and exploit the benefits of operating in hyperspace, including new booleanization strategies, optimization of TM inference and learning, as well as new TM applications.

Efficient Data Fusion using the Tsetlin Machine

We propose a novel way of assessing and fusing noisy dynamic data using a Tsetlin Machine. Our approach consists in monitoring how explanations in form of logical clauses that a TM learns changes with possible noise in dynamic data. This way TM can recognize the noise by lowering weights of previously learned clauses, or reflect it in the form of new clauses. We also perform a comprehensive experimental study using notably different datasets that demonstrated high performance of the proposed approach.

Building Concise Logical Patterns by Constraining Tsetlin Machine Clause Size

Tsetlin machine (TM) is a logic-based machine learning approach with the crucial advantages of being transparent and hardware-friendly. While TMs match or surpass deep learning accuracy for an increasing number of applications, large clause pools tend to produce clauses with many literals (long clauses). As such, they become less interpretable. Further, longer clauses increase the switching activity of the clause logic in hardware, consuming more power. This paper introduces a novel variant of TM learning - Clause Size Constrained TMs (CSC-TMs) - where one can set a soft constraint on the clause size. As soon as a clause includes more literals than the constraint allows, it starts expelling literals. Accordingly, oversized clauses only appear transiently. To evaluate CSC-TM, we conduct classification, clustering, and regression experiments on tabular data, natural language text, images, and board games. Our results show that CSC-TM maintains accuracy with up to 80 times fewer literals. Indeed, the accuracy increases with shorter clauses for TREC, IMDb, and BBC Sports. After the accuracy peaks, it drops gracefully as the clause size approaches a single literal. We finally analyze CSC-TM power consumption and derive new convergence properties.

A Relational Tsetlin Machine with Applications to Natural Language Understanding

TMs are a pattern recognition approach that uses finite state machines for learning and propositional logic to represent patterns. In addition to being natively interpretable, they have provided competitive accuracy for various tasks. In this paper, we increase the computing power of TMs by proposing a first-order logic-based framework with Herbrand semantics. The resulting TM is relational and can take advantage of logical structures appearing in natural language, to learn rules that represent how actions and consequences are related in the real world. The outcome is a logic program of Horn clauses, bringing in a structured view of unstructured data. In closed-domain question-answering, the first-order representation produces 10x more compact KBs, along with an increase in answering accuracy from 94.83% to 99.48%. The approach is further robust towards erroneous, missing, and superfluous information, distilling the aspects of a text that are important for real-world understanding.

Massively Parallel and Asynchronous Tsetlin Machine Architecture Supporting Almost Constant-Time Scaling

Using logical clauses to represent patterns, Tsetlin machines (TMs) have recently obtained competitive performance in terms of accuracy, memory footprint, energy, and learning speed on several benchmarks. A team of Tsetlin automata (TAs) composes each clause, thus driving the entire learning process. These are rewarded/penalized according to three local rules that optimize global behaviour. Each clause votes for or against a particular class, with classification resolved using a majority vote. In the parallel and asynchronous architecture that we propose here, every clause runs in its own thread for massive parallelism. For each training example, we keep track of the class votes obtained from the clauses in local voting tallies. The local voting tallies allow us to detach the processing of each clause from the rest of the clauses, supporting decentralized learning. Thus, rather than processing training examples one-by-one as in the original TM, the clauses access the training examples simultaneously, updating themselves and the local voting tallies in parallel. There is no synchronization among the clause threads, apart from atomic adds to the local voting tallies. Operating asynchronously, each team of TA will most of the time operate on partially calculated or outdated voting tallies. However, across diverse learning tasks, it turns out that our decentralized TM learning algorithm copes well with working on outdated data, resulting in no significant loss in learning accuracy. Further, we show that the approach provides up to 50 times faster learning. Finally, learning time is almost constant for reasonable clause amounts. For sufficiently large clause numbers, computation time increases approximately proportionally. Our parallel and asynchronous architecture thus allows processing of more massive datasets and operating with more clauses for higher accuracy.