Energy-Efficient Federated Learning for AIoT using Clustering Methods

While substantial research has been devoted to optimizing model performance, convergence rates, and communication efficiency, the energy implications of federated learning (FL) within Artificial Intelligence of Things (AIoT) scenarios are often overlooked in the existing literature. This study examines the energy consumed during the FL process, focusing on three main energy-intensive processes: pre-processing, communication, and local learning, all contributing to the overall energy footprint. We rely on the observation that device/client selection is crucial for speeding up the convergence of model training in a distributed AIoT setting and propose two clustering-informed methods. These clustering solutions are designed to group AIoT devices with similar label distributions, resulting in clusters composed of nearly heterogeneous devices. Hence, our methods alleviate the heterogeneity often encountered in real-world distributed learning applications. Throughout extensive numerical experimentation, we demonstrate that our clustering strategies typically achieve high convergence rates while maintaining low energy consumption when compared to other recent approaches available in the literature.

Probabilistic Forecasting for Network Resource Analysis in Integrated Terrestrial and Non-Terrestrial Networks

Efficient resource management is critical for Non-Terrestrial Networks (NTNs) to provide consistent, high-quality service in remote and under-served regions. While traditional single-point prediction methods, such as Long-Short Term Memory (LSTM), have been used in terrestrial networks, they often fall short in NTNs due to the complexity of satellite dynamics, signal latency and coverage variability. Probabilistic forecasting, which quantifies the uncertainties of the predictions, is a robust alternative. In this paper, we evaluate the application of probabilistic forecasting techniques, in particular SFF, to NTN resource allocation scenarios. Our results show their effectiveness in predicting bandwidth and capacity requirements in different NTN segments of probabilistic forecasting compared to single-point prediction techniques such as LSTM. The results show the potential of black probabilistic forecasting models to provide accurate and reliable predictions and to quantify their uncertainty, making them indispensable for optimizing NTN resource allocation. At the end of the paper, we also present application scenarios and a standardization roadmap for the use of probabilistic forecasting in integrated Terrestrial Network (TN)-NTN environments.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Learn More by Using Less: Distributed Learning with Energy-Constrained Devices

Federated Learning (FL) has emerged as a solution for distributed model training across decentralized, privacy-preserving devices, but the different energy capacities of participating devices (system heterogeneity) constrain real-world implementations. These energy limitations not only reduce model accuracy but also increase dropout rates, impacting on convergence in practical FL deployments. In this work, we propose LeanFed, an energy-aware FL framework designed to optimize client selection and training workloads on battery-constrained devices. LeanFed leverages adaptive data usage by dynamically adjusting the fraction of local data each device utilizes during training, thereby maximizing device participation across communication rounds while ensuring they do not run out of battery during the process. We rigorously evaluate LeanFed against traditional FedAvg on CIFAR-10 and CIFAR-100 datasets, simulating various levels of data heterogeneity and device participation rates. Results show that LeanFed consistently enhances model accuracy and stability, particularly in settings with high data heterogeneity and limited battery life, by mitigating client dropout and extending device availability. This approach demonstrates the potential of energy-efficient, privacy-preserving FL in real-world, large-scale applications, setting a foundation for robust and sustainable pervasive AI on resource-constrained networks.

Consistent Estimation of a Class of Distances Between Covariance Matrices

This work considers the problem of estimating the distance between two covariance matrices directly from the data. Particularly, we are interested in the family of distances that can be expressed as sums of traces of functions that are separately applied to each covariance matrix. This family of distances is particularly useful as it takes into consideration the fact that covariance matrices lie in the Riemannian manifold of positive definite matrices, thereby including a variety of commonly used metrics, such as the Euclidean distance, Jeffreys' divergence, and the log-Euclidean distance. Moreover, a statistical analysis of the asymptotic behavior of this class of distance estimators has also been conducted. Specifically, we present a central limit theorem that establishes the asymptotic Gaussianity of these estimators and provides closed form expressions for the corresponding means and variances. Empirical evaluations demonstrate the superiority of our proposed consistent estimator over conventional plug-in estimators in multivariate analytical contexts. Additionally, the central limit theorem derived in this study provides a robust statistical framework to assess of accuracy of these estimators.

Statistical Framework for Clustering MU-MIMO Wireless via Second Order Statistics

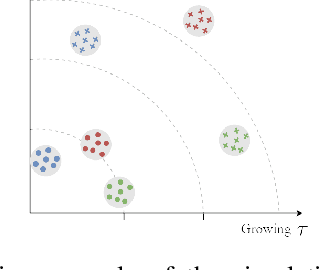
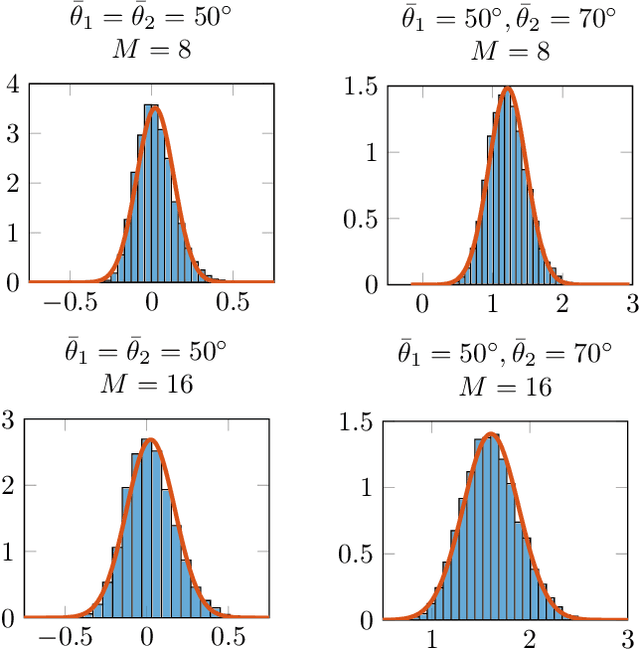
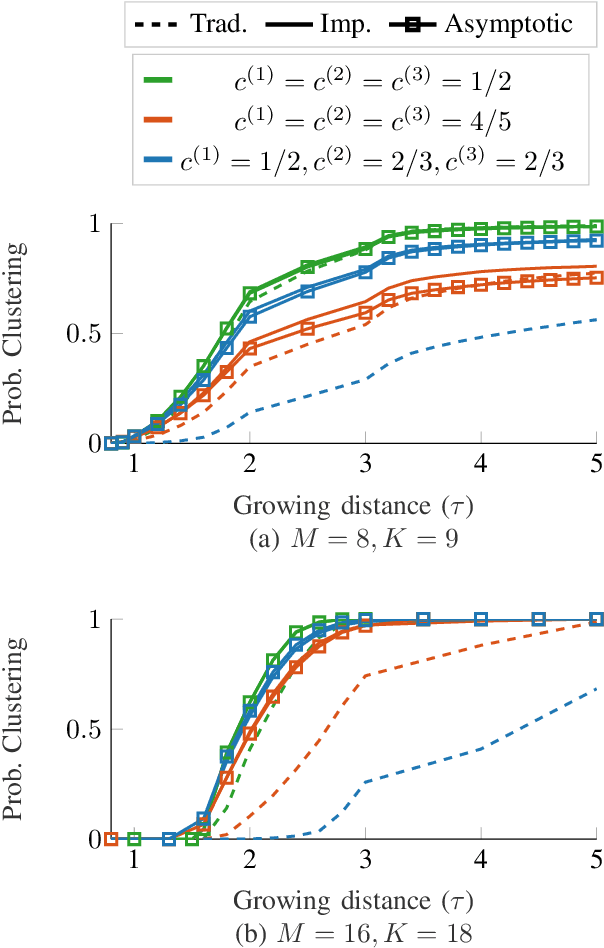
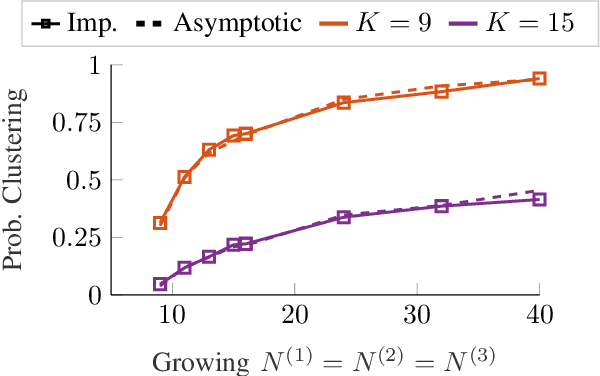
This work explores the clustering of wireless users by examining the distances between their channel covariance matrices, which reside on the Riemannian manifold of positive definite matrices. Specifically, we consider an estimator of the Log-Euclidean distance between multiple sample covariance matrices (SCMs) consistent when the number of samples and the observation size grow unbounded at the same rate. Within the context of multi-user MIMO (MU-MIMO) wireless communication systems, we develop a statistical framework that allows to accurate predictions of the clustering algorithm's performance under realistic conditions. Specifically, we present a central limit theorem that establishes the asymptotic Gaussianity of the consistent estimator of the log-Euclidean distance computed over two sample covariance matrices.

Deterministic Equivalent of the Log-Euclidean Distance between Sample Covariance Matrices

Log-Euclidean distances are commonly used to quantify the similarity between positive definite matrices using geometric considerations. This paper analyzes the behavior of this distance when it is used to measure closeness between independent sample covariance matrices. A closed form expression is given for the deterministic equivalent of such distance, which asymptotically approximates the actual distance in the large observation regime (both sample size and observation dimension grow to infinity at the same rate). The deterministic equivalent can be used to analyze the performance of the log-Euclidean metric when compared to other commonly used metrics such as the Euclidean norm or the symmetrized Kullback-Leibler divergence.

F-KANs: Federated Kolmogorov-Arnold Networks

In this paper, we present an innovative federated learning (FL) approach that utilizes Kolmogorov-Arnold Networks (KANs) for classification tasks. By utilizing the adaptive activation capabilities of KANs in a federated framework, we aim to improve classification capabilities while preserving privacy. The study evaluates the performance of federated KANs (F- KANs) compared to traditional Multi-Layer Perceptrons (MLPs) on classification task. The results show that the F-KANs model significantly outperforms the federated MLP model in terms of accuracy, precision, recall, F1 score and stability, and achieves better performance, paving the way for more efficient and privacy-preserving predictive analytics.

Kolmogorov-Arnold Networks (KANs) for Time Series Analysis

This paper introduces a novel application of Kolmogorov-Arnold Networks (KANs) to time series forecasting, leveraging their adaptive activation functions for enhanced predictive modeling. Inspired by the Kolmogorov-Arnold representation theorem, KANs replace traditional linear weights with spline-parametrized univariate functions, allowing them to learn activation patterns dynamically. We demonstrate that KANs outperforms conventional Multi-Layer Perceptrons (MLPs) in a real-world satellite traffic forecasting task, providing more accurate results with considerably fewer number of learnable parameters. We also provide an ablation study of KAN-specific parameters impact on performance. The proposed approach opens new avenues for adaptive forecasting models, emphasizing the potential of KANs as a powerful tool in predictive analytics.

Asymptotics of Distances Between Sample Covariance Matrices

This work considers the asymptotic behavior of the distance between two sample covariance matrices (SCM). A general result is provided for a class of functionals that can be expressed as sums of traces of functions that are separately applied to each covariance matrix. In particular, this class includes very conventional metrics, such as the Euclidean distance or Jeffrery's divergence, as well as a number of other more sophisticated distances recently derived from Riemannian geometry considerations, such as the log-Euclidean metric. In particular, we analyze the asymptotic behavior of this class of functionals by establishing a central limit theorem that allows us to describe their asymptotic statistical law. In order to account for the fact that the sample sizes of two SCMs are of the same order of magnitude as their observation dimension, results are provided by assuming that these parameters grow to infinity while their quotients converge to fixed quantities. Numerical results illustrate how this type of result can be used in order to predict the performance of these metrics in practical machine learning algorithms, such as clustering of SCMs.