Xavier Mestre
Beamfocusing Capabilities of a Uniform Linear Array in the Holographic Regime
Feb 11, 2025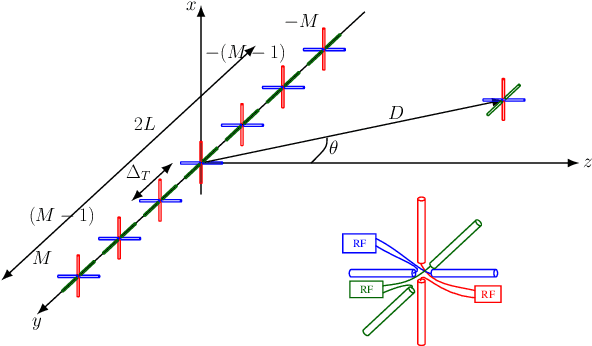
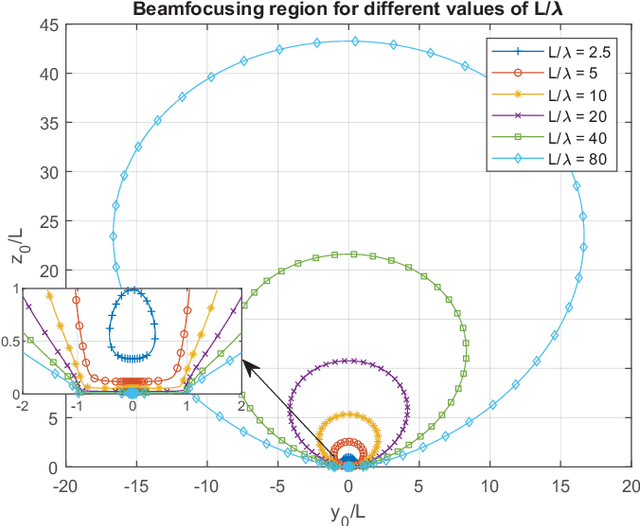
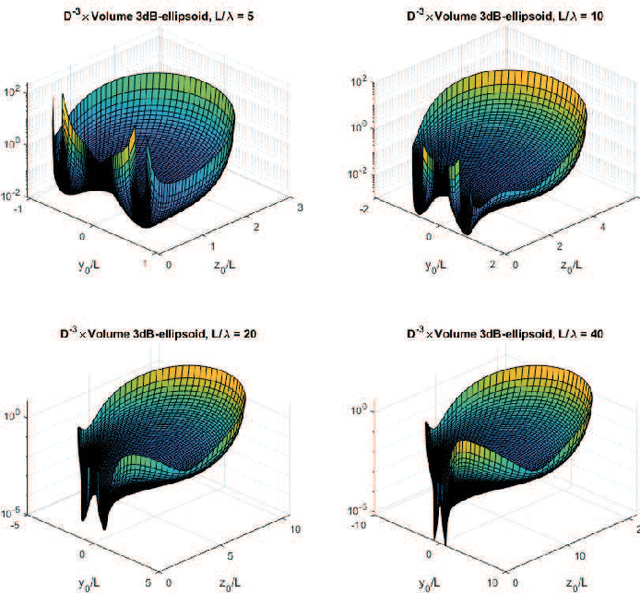
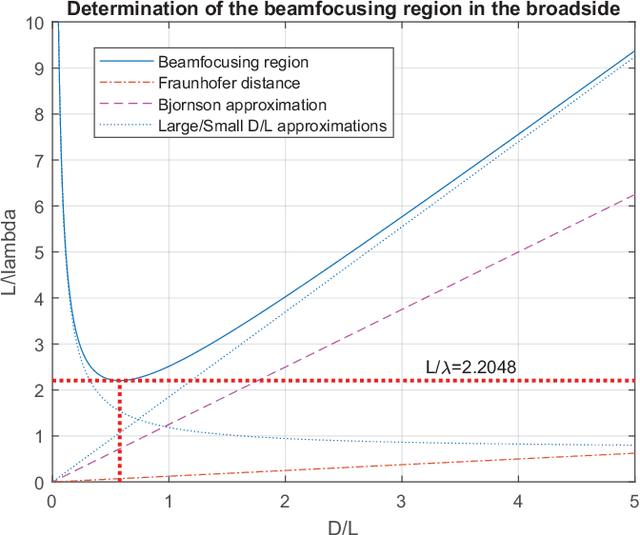
Abstract:The use of multiantenna technologies in the near field offers the possibility of focusing the energy in spatial regions rather than just in angle. The objective of this paper is to provide a formal framework that allows to establish the region in space where this effect can take place and how efficient this focusing can be, assuming that the transmit architecture is a uniform linear array (ULA). A dyadic Green's channel model is adopted, and the amplitude differences between the receiver and each transmit antenna are effectively incorporated in the model. By considering a second-order expansion of the SNR around the intended receiver, a formal criterion is derived in order to establish whether beamfocusing is feasible or not. An analytic description is provided that determines the shape and position of the asymptotic ellipsoid where a minimum SNR is achieved. Further insights are provided by considering the holographic regime, whereby the number of elements of the ULA increase without bound while the distance between adjacent elements converges to zero. This asymptotic framework allows to simplify the analytical form of the beamfocusing feasibility region, which in turn provides some further insights into the shape of the coverage regions depending on the position of the intended receiver. In particular, it is shown that beamfocusing is only possible if the size of the ULA is at least $4.4\lambda$ where $\lambda$ is the transmission wavelength. Furthermore, a closed form analytical expression is provided that asymptotically determines the maximum distance where beamfocusing is feasible as a function of the elevation angle. In particular, beamfocusing is only feasible when the receiver is located between a minimum and a maximum distance from the array, where these upper and lower distance limits effectively depend on the angle of elevation
Available Degrees of Spatial Multiplexing of a Uniform Linear Array with Multiple Polarizations: a Holographic Perspective
Oct 25, 2024Abstract:The capabilities of multi-antenna technology have recently been significantly enhanced by the proliferation of extra large array architectures. The high dimensionality of these systems implies that communications take place in the nearfield regime, which poses some questions as to their effective perfomrance even under simple line of sight configurations. In order to study these limitations, a uniform linear array (ULA) is considered here, the elements of which are three infinitesimal dipoles transmitting different signals in the three spatial dimensions. The receiver consists of a single element with three orthogonal infinitesimal dipoles and full channel state information is assumed to be available at both ends. A capacity analysis is presented when the number of elements of the ULA increases without bound while the interelement distance converges to zero, so that the total aperture length is kept asymptotically fixed. In particular, the total number of available spatial eigenmodes is shown to depend crucially on the receiver position in space, and closed form expressions are provided for the different achievability regions. From the analysis it can be concluded that the use of three orthogonal polarizations at the transmitter guarantees the almost universal availability of two spatial streams, whereas the use of only two polarizations results in a more extensive region where maximum multiplexing gain is available.
Exploiting Multiple Polarizations in Extra Large Holographic MIMO
Oct 11, 2024Abstract:The proliferation of large multi-antenna configurations operating in high frequency bands has recently challenged the conventional far-field, rich-scattering paradigm of wireless channels. Extra large antenna arrays must usually work in the near field and in the absence of multipath, which are far from traditional assumptions in conventional wireless communication systems. The present study proposes to analyze the spatial multiplexing capabilities of large multi-antenna configurations under line-of-sight, near field conditions by considering the use of multiple orthogonal diversities at both transmitter and receiver. The analysis is carried out using a holographic approximation to the problem, whereby the number of radiating elements is assumed to become large while their separation becomes asymptotically negligible. This emulates the operation of a continuous aperture of infinitesimal radiating elements, also recently known as holographic surfaces. The present study characterizes the asymptotic MIMO channel as seen by extra large uniform linear and planar arrays, as well as their associated achievable rates assuming access to perfect channel state information (CSI). It is shown, in particular, that for a given distance between the receiver and the center of the array and a given signal quality, there exists an optimum dimension of the multi-antenna surface that maximizes the spectral efficiency.
Consistent Estimation of a Class of Distances Between Covariance Matrices
Sep 18, 2024Abstract:This work considers the problem of estimating the distance between two covariance matrices directly from the data. Particularly, we are interested in the family of distances that can be expressed as sums of traces of functions that are separately applied to each covariance matrix. This family of distances is particularly useful as it takes into consideration the fact that covariance matrices lie in the Riemannian manifold of positive definite matrices, thereby including a variety of commonly used metrics, such as the Euclidean distance, Jeffreys' divergence, and the log-Euclidean distance. Moreover, a statistical analysis of the asymptotic behavior of this class of distance estimators has also been conducted. Specifically, we present a central limit theorem that establishes the asymptotic Gaussianity of these estimators and provides closed form expressions for the corresponding means and variances. Empirical evaluations demonstrate the superiority of our proposed consistent estimator over conventional plug-in estimators in multivariate analytical contexts. Additionally, the central limit theorem derived in this study provides a robust statistical framework to assess of accuracy of these estimators.
Statistical Framework for Clustering MU-MIMO Wireless via Second Order Statistics
Aug 08, 2024
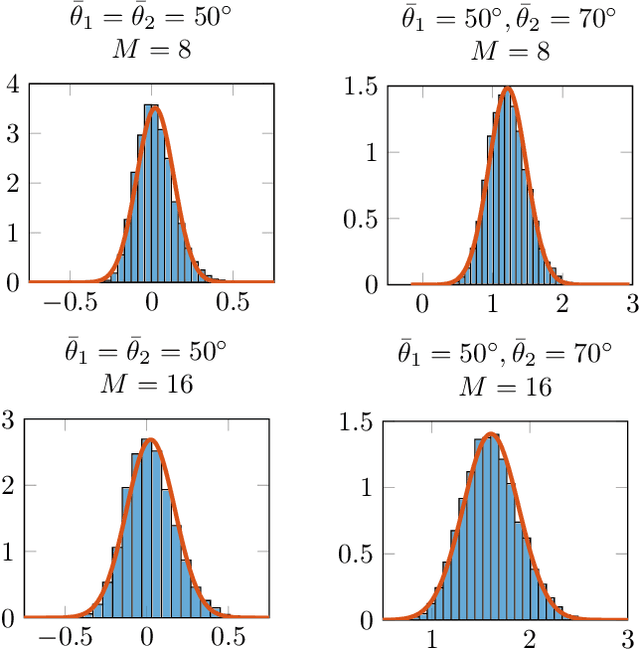
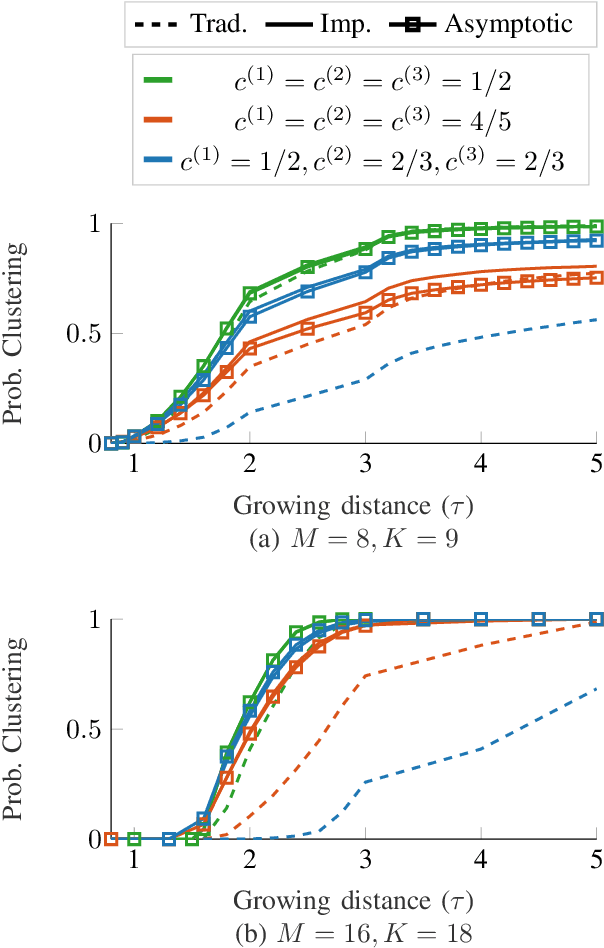
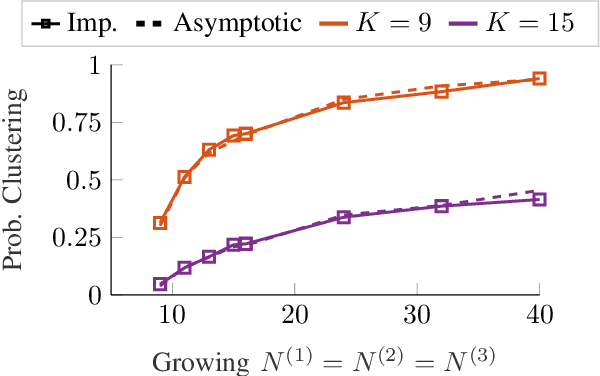
Abstract:This work explores the clustering of wireless users by examining the distances between their channel covariance matrices, which reside on the Riemannian manifold of positive definite matrices. Specifically, we consider an estimator of the Log-Euclidean distance between multiple sample covariance matrices (SCMs) consistent when the number of samples and the observation size grow unbounded at the same rate. Within the context of multi-user MIMO (MU-MIMO) wireless communication systems, we develop a statistical framework that allows to accurate predictions of the clustering algorithm's performance under realistic conditions. Specifically, we present a central limit theorem that establishes the asymptotic Gaussianity of the consistent estimator of the log-Euclidean distance computed over two sample covariance matrices.
Deterministic Equivalent of the Log-Euclidean Distance between Sample Covariance Matrices
Aug 08, 2024Abstract:Log-Euclidean distances are commonly used to quantify the similarity between positive definite matrices using geometric considerations. This paper analyzes the behavior of this distance when it is used to measure closeness between independent sample covariance matrices. A closed form expression is given for the deterministic equivalent of such distance, which asymptotically approximates the actual distance in the large observation regime (both sample size and observation dimension grow to infinity at the same rate). The deterministic equivalent can be used to analyze the performance of the log-Euclidean metric when compared to other commonly used metrics such as the Euclidean norm or the symmetrized Kullback-Leibler divergence.
Asymptotics of Distances Between Sample Covariance Matrices
Dec 22, 2023Abstract:This work considers the asymptotic behavior of the distance between two sample covariance matrices (SCM). A general result is provided for a class of functionals that can be expressed as sums of traces of functions that are separately applied to each covariance matrix. In particular, this class includes very conventional metrics, such as the Euclidean distance or Jeffrery's divergence, as well as a number of other more sophisticated distances recently derived from Riemannian geometry considerations, such as the log-Euclidean metric. In particular, we analyze the asymptotic behavior of this class of functionals by establishing a central limit theorem that allows us to describe their asymptotic statistical law. In order to account for the fact that the sample sizes of two SCMs are of the same order of magnitude as their observation dimension, results are provided by assuming that these parameters grow to infinity while their quotients converge to fixed quantities. Numerical results illustrate how this type of result can be used in order to predict the performance of these metrics in practical machine learning algorithms, such as clustering of SCMs.
Near-Field Beamfocusing with Polarized Antennas
Nov 30, 2023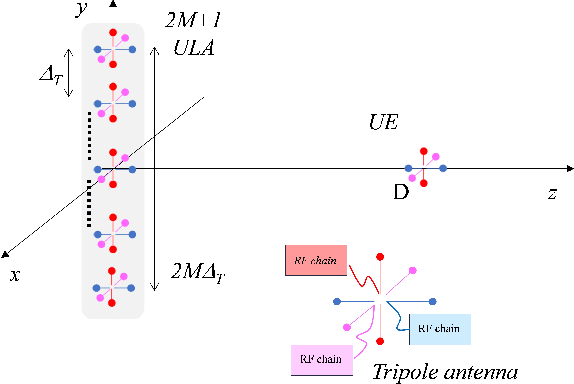
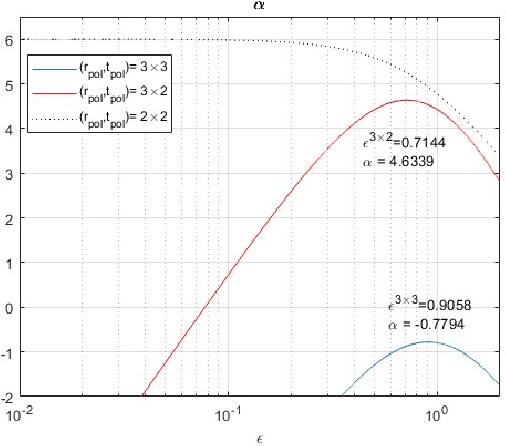
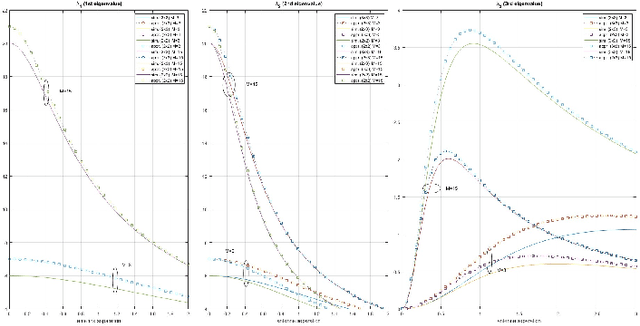
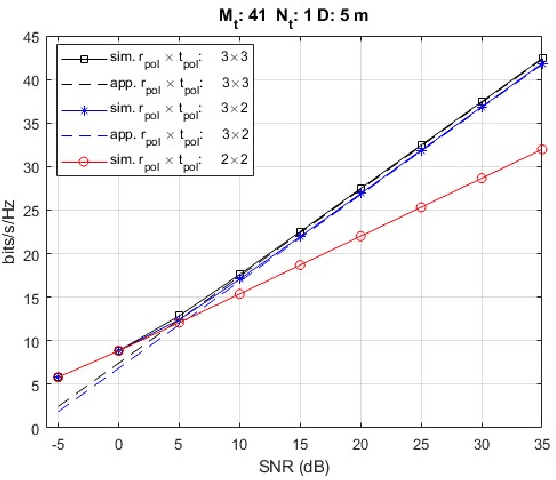
Abstract:One of the most relevant challenges in future 6G wireless networks is how to support a massive spatial multiplexing of a large number of user terminals. Recently, extremely large antenna arrays (ELAAs), also referred to as extra-large MIMO (XL-MIMO), have emerged as an potential enabler of this type of spatially multiplexed transmission. These massive configurations substantially increase the number of available spatial degrees of freedom (transmission modes) while also enabling to spatially focus the transmitted energy into a very small region, thanks to the properties of near-field propagation and the large number of transmitters. This work explores whether multiplexing of multiple orthogonal polarizations can enhance the system performance in the near-field. We concentrate on a simple scenario consisting of a Uniform Linear Array (ULA) and a single antenna element user equipment (UE). We demonstrate that the number of spatial degrees of freedom can be as large as 3 in the near-field of a Line of Sight (LoS) channel when both transmitter and receiver employ three orthogonal linear polarizations. In the far-field, however, the maximum number of spatial degrees of freedom tends to be only 2, due to the fact that the equivalent MIMO channel becomes rank deficient. We provide an analytical approximation to the achievable rate, which allows us to derive approximations to the optimal antenna spacing and array size that maximize the achievable rate
Energy-Saving Cell-Free Massive MIMO Precoders with a Per-AP Wideband Kronecker Channel Model
Sep 27, 2023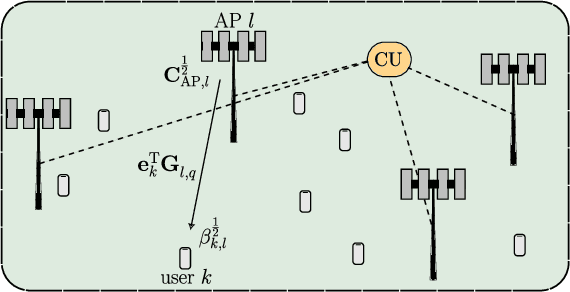
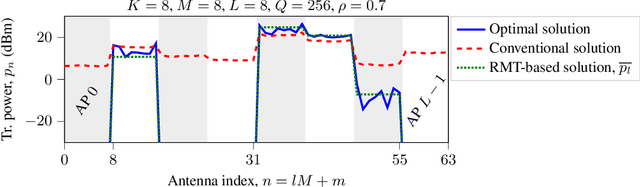
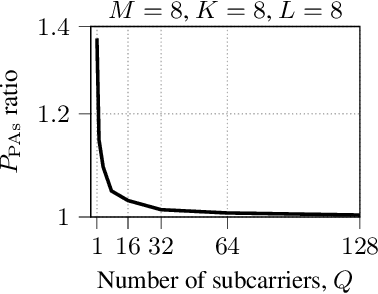
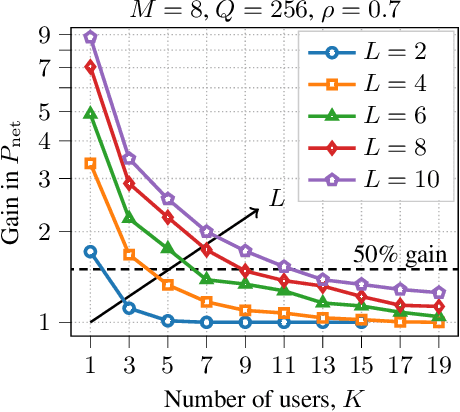
Abstract:We study cell-free massive multiple-input multiple-output precoders that minimize the power consumed by the power amplifiers subject to per-user per-subcarrier rate constraints. The power at each antenna is generally retrieved by solving a fixed-point equation that depends on the instantaneous channel coefficients. Using random matrix theory, we retrieve each antenna power as the solution to a fixed-point equation that depends only on the second-order statistics of the channel. Numerical simulations prove the accuracy of our asymptotic approximation and show how a subset of access points should be turned off to save power consumption, while all the antennas of the active access points are utilized with uniform power across them. This mechanism allows to save consumed power up to a factor of 9$\times$ in low-load scenarios.
Deep Unfolding for Fast Linear Massive MIMO Precoders under a PA Consumption Model
Apr 25, 2023Abstract:Massive multiple-input multiple-output (MIMO) precoders are typically designed by minimizing the transmit power subject to a quality-of-service (QoS) constraint. However, current sustainability goals incentivize more energy-efficient solutions and thus it is of paramount importance to minimize the consumed power directly. Minimizing the consumed power of the power amplifier (PA), one of the most consuming components, gives rise to a convex, non-differentiable optimization problem, which has been solved in the past using conventional convex solvers. Additionally, this problem can be solved using a proximal gradient descent (PGD) algorithm, which suffers from slow convergence. In this work, to overcome the slow convergence, a deep unfolded version of the algorithm is proposed, which can achieve close-to-optimal solutions in only 20 iterations compared to the 3500 plus iterations needed by the PGD algorithm. Results indicate that the deep unfolding algorithm is three orders of magnitude faster than a conventional convex solver and four orders of magnitude faster than the PGD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge