Beamfocusing Capabilities of a Uniform Linear Array in the Holographic Regime

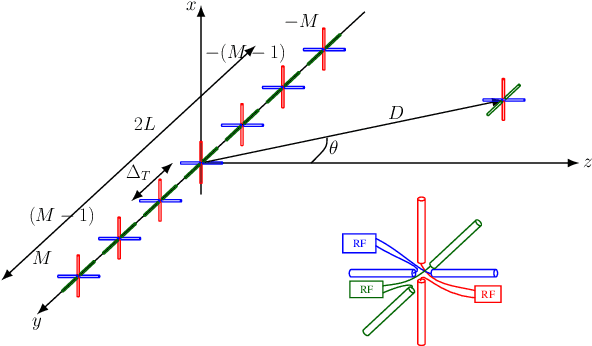
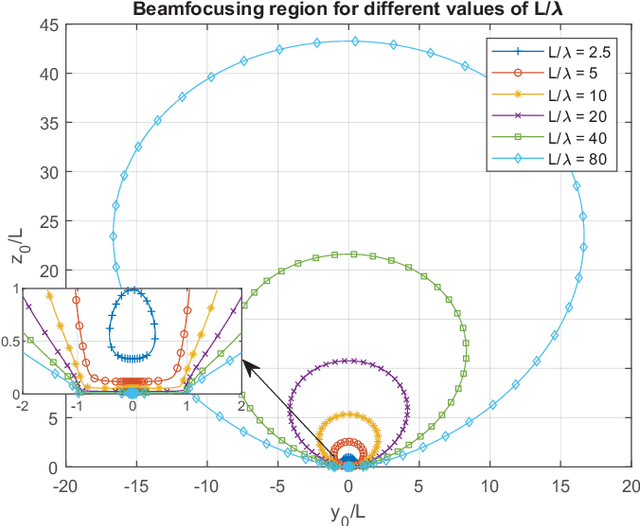
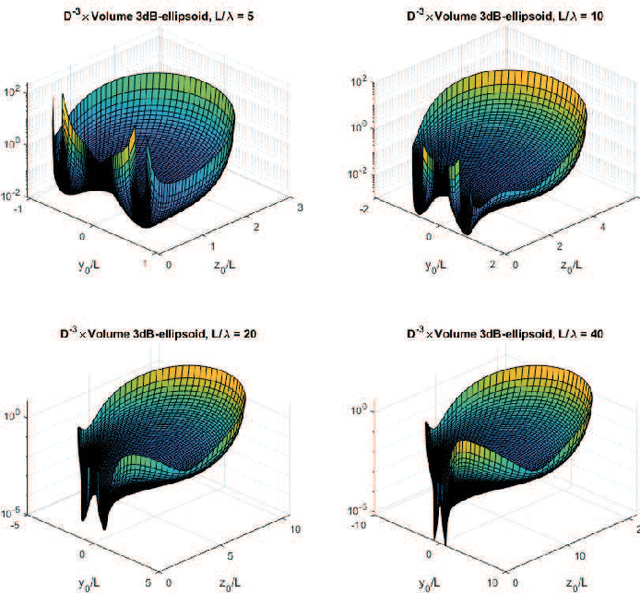
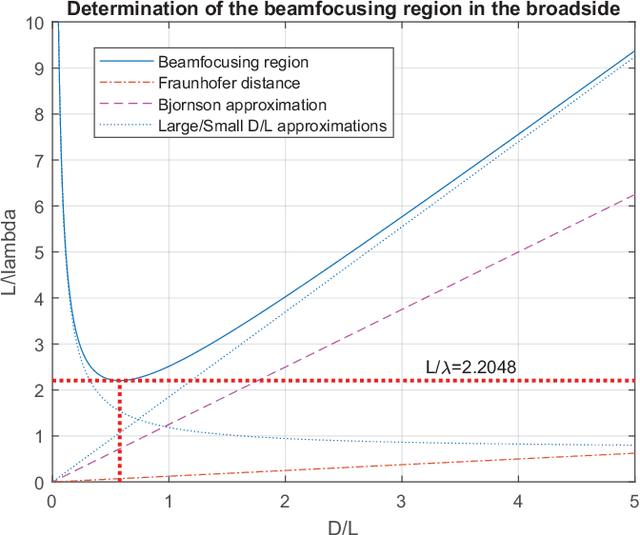
The use of multiantenna technologies in the near field offers the possibility of focusing the energy in spatial regions rather than just in angle. The objective of this paper is to provide a formal framework that allows to establish the region in space where this effect can take place and how efficient this focusing can be, assuming that the transmit architecture is a uniform linear array (ULA). A dyadic Green's channel model is adopted, and the amplitude differences between the receiver and each transmit antenna are effectively incorporated in the model. By considering a second-order expansion of the SNR around the intended receiver, a formal criterion is derived in order to establish whether beamfocusing is feasible or not. An analytic description is provided that determines the shape and position of the asymptotic ellipsoid where a minimum SNR is achieved. Further insights are provided by considering the holographic regime, whereby the number of elements of the ULA increase without bound while the distance between adjacent elements converges to zero. This asymptotic framework allows to simplify the analytical form of the beamfocusing feasibility region, which in turn provides some further insights into the shape of the coverage regions depending on the position of the intended receiver. In particular, it is shown that beamfocusing is only possible if the size of the ULA is at least $4.4\lambda$ where $\lambda$ is the transmission wavelength. Furthermore, a closed form analytical expression is provided that asymptotically determines the maximum distance where beamfocusing is feasible as a function of the elevation angle. In particular, beamfocusing is only feasible when the receiver is located between a minimum and a maximum distance from the array, where these upper and lower distance limits effectively depend on the angle of elevation