Beamfocusing Capabilities of a Uniform Linear Array in the Holographic Regime

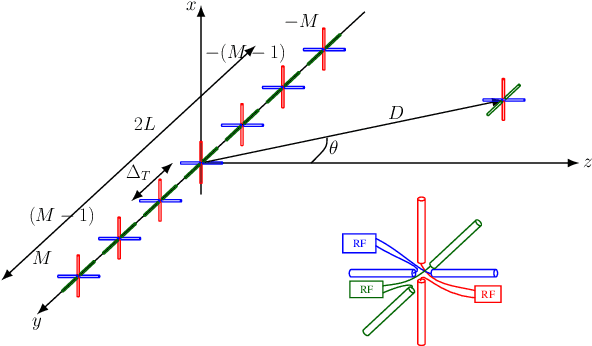
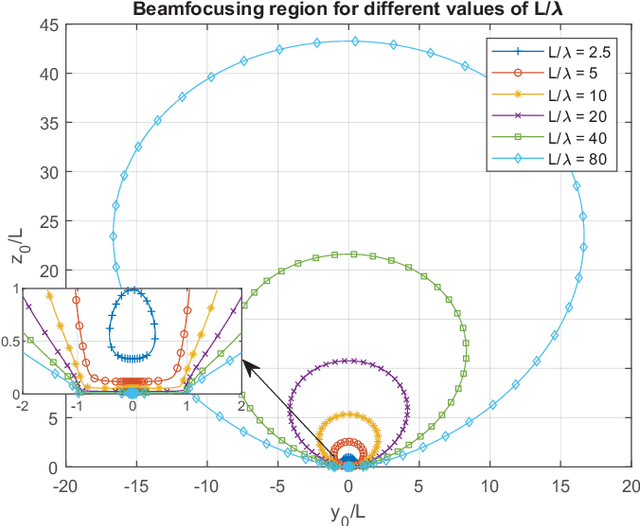
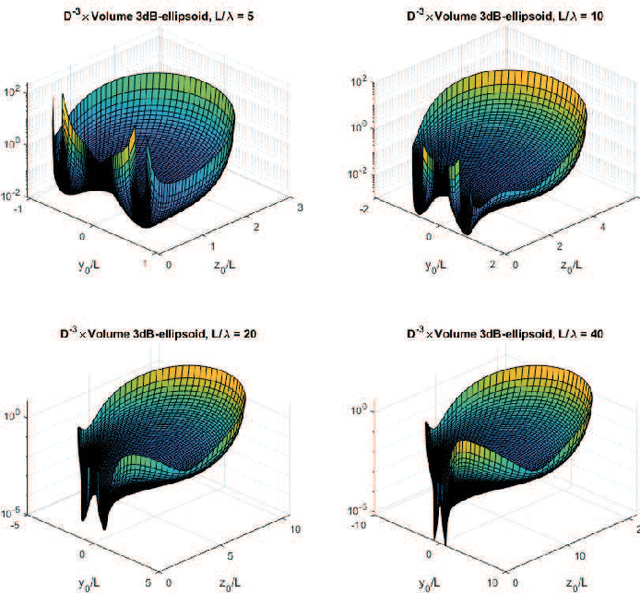
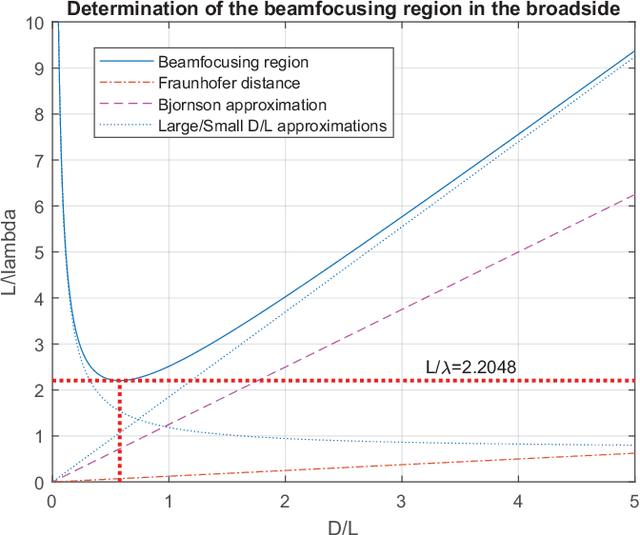
The use of multiantenna technologies in the near field offers the possibility of focusing the energy in spatial regions rather than just in angle. The objective of this paper is to provide a formal framework that allows to establish the region in space where this effect can take place and how efficient this focusing can be, assuming that the transmit architecture is a uniform linear array (ULA). A dyadic Green's channel model is adopted, and the amplitude differences between the receiver and each transmit antenna are effectively incorporated in the model. By considering a second-order expansion of the SNR around the intended receiver, a formal criterion is derived in order to establish whether beamfocusing is feasible or not. An analytic description is provided that determines the shape and position of the asymptotic ellipsoid where a minimum SNR is achieved. Further insights are provided by considering the holographic regime, whereby the number of elements of the ULA increase without bound while the distance between adjacent elements converges to zero. This asymptotic framework allows to simplify the analytical form of the beamfocusing feasibility region, which in turn provides some further insights into the shape of the coverage regions depending on the position of the intended receiver. In particular, it is shown that beamfocusing is only possible if the size of the ULA is at least $4.4\lambda$ where $\lambda$ is the transmission wavelength. Furthermore, a closed form analytical expression is provided that asymptotically determines the maximum distance where beamfocusing is feasible as a function of the elevation angle. In particular, beamfocusing is only feasible when the receiver is located between a minimum and a maximum distance from the array, where these upper and lower distance limits effectively depend on the angle of elevation

Available Degrees of Spatial Multiplexing of a Uniform Linear Array with Multiple Polarizations: a Holographic Perspective

The capabilities of multi-antenna technology have recently been significantly enhanced by the proliferation of extra large array architectures. The high dimensionality of these systems implies that communications take place in the nearfield regime, which poses some questions as to their effective perfomrance even under simple line of sight configurations. In order to study these limitations, a uniform linear array (ULA) is considered here, the elements of which are three infinitesimal dipoles transmitting different signals in the three spatial dimensions. The receiver consists of a single element with three orthogonal infinitesimal dipoles and full channel state information is assumed to be available at both ends. A capacity analysis is presented when the number of elements of the ULA increases without bound while the interelement distance converges to zero, so that the total aperture length is kept asymptotically fixed. In particular, the total number of available spatial eigenmodes is shown to depend crucially on the receiver position in space, and closed form expressions are provided for the different achievability regions. From the analysis it can be concluded that the use of three orthogonal polarizations at the transmitter guarantees the almost universal availability of two spatial streams, whereas the use of only two polarizations results in a more extensive region where maximum multiplexing gain is available.

Exploiting Multiple Polarizations in Extra Large Holographic MIMO

The proliferation of large multi-antenna configurations operating in high frequency bands has recently challenged the conventional far-field, rich-scattering paradigm of wireless channels. Extra large antenna arrays must usually work in the near field and in the absence of multipath, which are far from traditional assumptions in conventional wireless communication systems. The present study proposes to analyze the spatial multiplexing capabilities of large multi-antenna configurations under line-of-sight, near field conditions by considering the use of multiple orthogonal diversities at both transmitter and receiver. The analysis is carried out using a holographic approximation to the problem, whereby the number of radiating elements is assumed to become large while their separation becomes asymptotically negligible. This emulates the operation of a continuous aperture of infinitesimal radiating elements, also recently known as holographic surfaces. The present study characterizes the asymptotic MIMO channel as seen by extra large uniform linear and planar arrays, as well as their associated achievable rates assuming access to perfect channel state information (CSI). It is shown, in particular, that for a given distance between the receiver and the center of the array and a given signal quality, there exists an optimum dimension of the multi-antenna surface that maximizes the spectral efficiency.

Near-Field Beamfocusing with Polarized Antennas

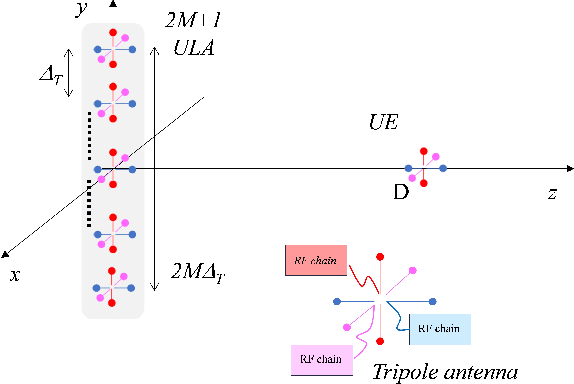
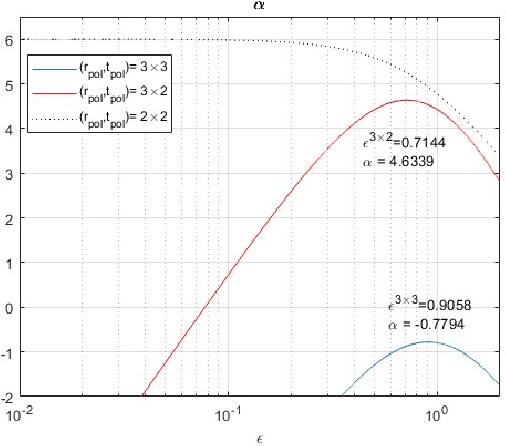
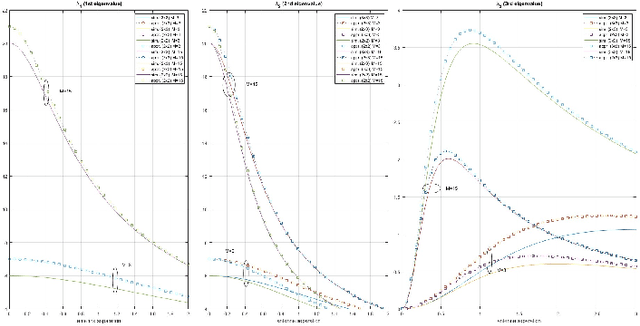
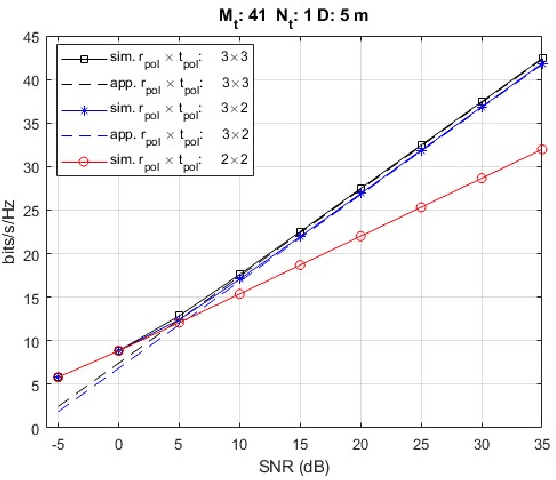
One of the most relevant challenges in future 6G wireless networks is how to support a massive spatial multiplexing of a large number of user terminals. Recently, extremely large antenna arrays (ELAAs), also referred to as extra-large MIMO (XL-MIMO), have emerged as an potential enabler of this type of spatially multiplexed transmission. These massive configurations substantially increase the number of available spatial degrees of freedom (transmission modes) while also enabling to spatially focus the transmitted energy into a very small region, thanks to the properties of near-field propagation and the large number of transmitters. This work explores whether multiplexing of multiple orthogonal polarizations can enhance the system performance in the near-field. We concentrate on a simple scenario consisting of a Uniform Linear Array (ULA) and a single antenna element user equipment (UE). We demonstrate that the number of spatial degrees of freedom can be as large as 3 in the near-field of a Line of Sight (LoS) channel when both transmitter and receiver employ three orthogonal linear polarizations. In the far-field, however, the maximum number of spatial degrees of freedom tends to be only 2, due to the fact that the equivalent MIMO channel becomes rank deficient. We provide an analytical approximation to the achievable rate, which allows us to derive approximations to the optimal antenna spacing and array size that maximize the achievable rate