Asymptotics of Distances Between Sample Covariance Matrices

This work considers the asymptotic behavior of the distance between two sample covariance matrices (SCM). A general result is provided for a class of functionals that can be expressed as sums of traces of functions that are separately applied to each covariance matrix. In particular, this class includes very conventional metrics, such as the Euclidean distance or Jeffrery's divergence, as well as a number of other more sophisticated distances recently derived from Riemannian geometry considerations, such as the log-Euclidean metric. In particular, we analyze the asymptotic behavior of this class of functionals by establishing a central limit theorem that allows us to describe their asymptotic statistical law. In order to account for the fact that the sample sizes of two SCMs are of the same order of magnitude as their observation dimension, results are provided by assuming that these parameters grow to infinity while their quotients converge to fixed quantities. Numerical results illustrate how this type of result can be used in order to predict the performance of these metrics in practical machine learning algorithms, such as clustering of SCMs.

Mathematical Properties of the Zadoff-Chu Sequences

This paper is a compilation of well-known results about Zadoff-Chu sequences, including all proofs with a consistent mathematical notation, for easy reference. Moreover, for a Zadoff-Chu sequence $x_u[n]$ of prime length $N_{\text{ZC}}$ and root index $u$, a formula is derived that allows computing the first term (frequency zero) of its discrete Fourier transform, $X_u[0]$, with constant complexity independent of the sequence length, as opposed to accumulating all its $N_{\text{ZC}}$ terms. The formula stems from a famous result in analytic number theory and is an interesting complement to the fact that the discrete Fourier transform of a Zadoff-Chu sequence is itself a Zadoff-Chu sequence whose terms are scaled by $X_u[0]$. Finally, the paper concludes with a brief analysis of time-continuous signals derived from Zadoff-Chu sequences, especially those obtained by OFDM-modulating a Zadoff-Chu sequence.

Floor Map Reconstruction Through Radio Sensing and Learning By a Large Intelligent Surface

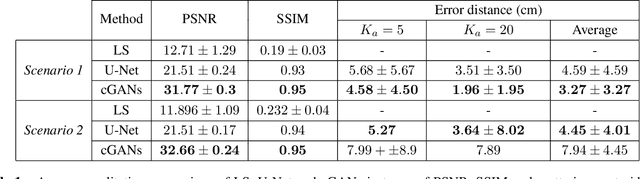
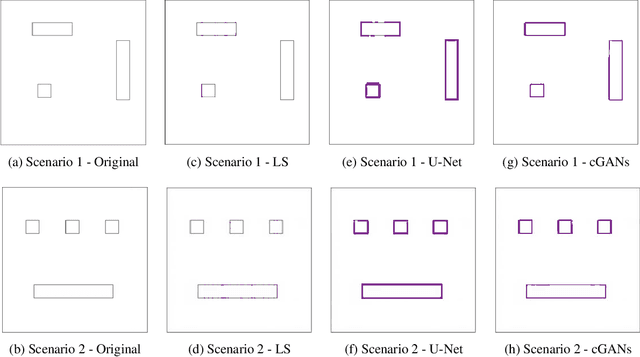
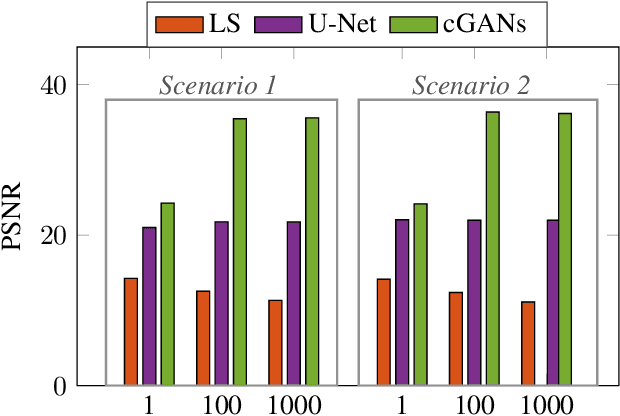
Environmental scene reconstruction is of great interest for autonomous robotic applications, since an accurate representation of the environment is necessary to ensure safe interaction with robots. Equally important, it is also vital to ensure reliable communication between the robot and its controller. Large Intelligent Surface (LIS) is a technology that has been extensively studied due to its communication capabilities. Moreover, due to the number of antenna elements, these surfaces arise as a powerful solution to radio sensing. This paper presents a novel method to translate radio environmental maps obtained at the LIS to floor plans of the indoor environment built of scatterers spread along its area. The usage of a Least Squares (LS) based method, U-Net (UN) and conditional Generative Adversarial Networks (cGANs) were leveraged to perform this task. We show that the floor plan can be correctly reconstructed using both local and global measurements.

User Clustering for Rate Splitting using Machine Learning

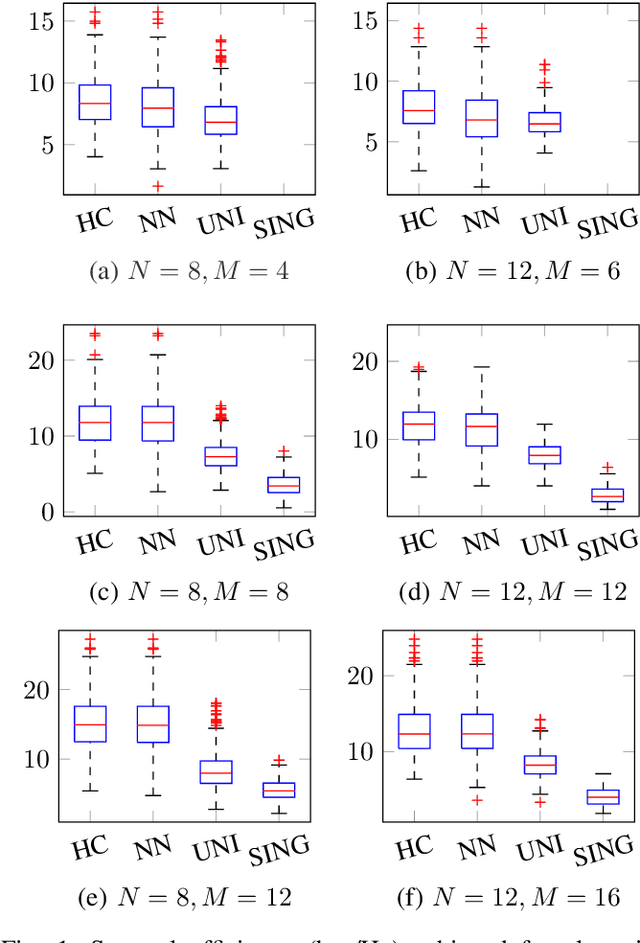
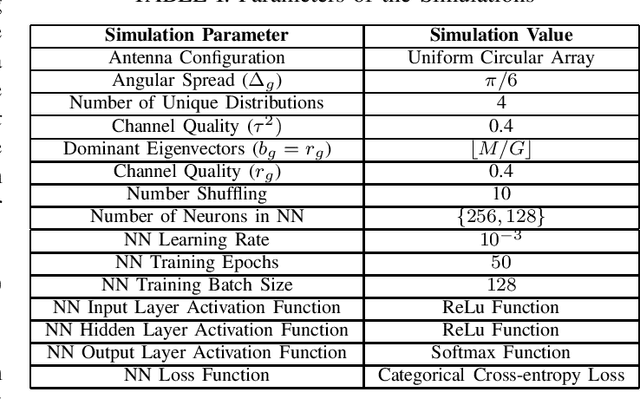
Hierarchical Rate Splitting (HRS) schemes proposed in recent years have shown to provide significant improvements in exploiting spatial diversity in wireless networks and provide high throughput for all users while minimising interference among them. Hence, one of the major challenges for such HRS schemes is the necessity to know the optimal clustering of these users based only on their Channel State Information (CSI). This clustering problem is known to be NP hard and, to deal with the unmanageable complexity of finding an optimal solution, in this work a scalable and much lighter clustering mechanism based on Neural Network (NN) is proposed. The accuracy and performance metrics show that the NN is able to learn and cluster the users based on the noisy channel response and is able to achieve a rate comparable to other more complex clustering schemes from the literature.

Exclusive Group Lasso for Structured Variable Selection

A structured variable selection problem is considered in which the covariates, divided into predefined groups, activate according to sparse patterns with few nonzero entries per group. Capitalizing on the concept of atomic norm, a composite norm can be properly designed to promote such exclusive group sparsity patterns. The resulting norm lends itself to efficient and flexible regularized optimization algorithms for support recovery, like the proximal algorithm. Moreover, an active set algorithm is proposed that builds the solution by successively including structure atoms into the estimated support. It is also shown that such an algorithm can be tailored to match more rigid structures than plain exclusive group sparsity. Asymptotic consistency analysis (with both the number of parameters as well as the number of groups growing with the observation size) establishes the effectiveness of the proposed solution in terms of signed support recovery under conventional assumptions. Finally, a set of numerical simulations further corroborates the results.