Energy-Saving Cell-Free Massive MIMO Precoders with a Per-AP Wideband Kronecker Channel Model
Paper and Code
Sep 27, 2023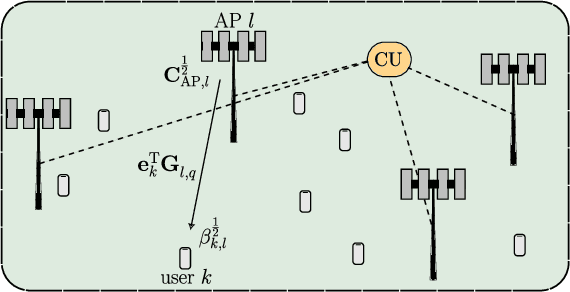
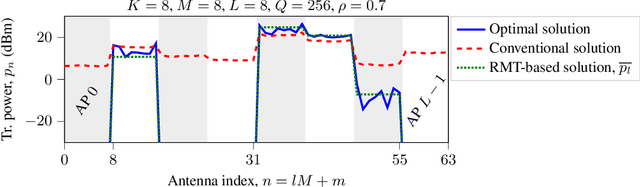
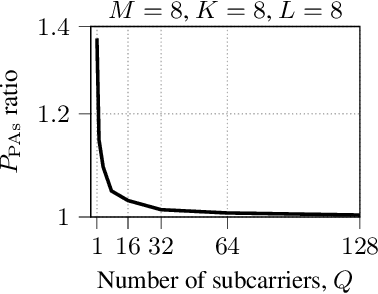
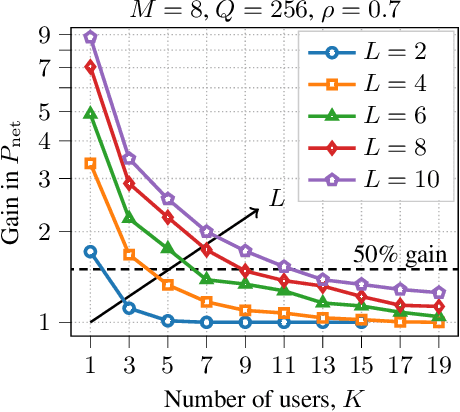
We study cell-free massive multiple-input multiple-output precoders that minimize the power consumed by the power amplifiers subject to per-user per-subcarrier rate constraints. The power at each antenna is generally retrieved by solving a fixed-point equation that depends on the instantaneous channel coefficients. Using random matrix theory, we retrieve each antenna power as the solution to a fixed-point equation that depends only on the second-order statistics of the channel. Numerical simulations prove the accuracy of our asymptotic approximation and show how a subset of access points should be turned off to save power consumption, while all the antennas of the active access points are utilized with uniform power across them. This mechanism allows to save consumed power up to a factor of 9$\times$ in low-load scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge