PB$^2$: Preference Space Exploration via Population-Based Methods in Preference-Based Reinforcement Learning

Preference-based reinforcement learning (PbRL) has emerged as a promising approach for learning behaviors from human feedback without predefined reward functions. However, current PbRL methods face a critical challenge in effectively exploring the preference space, often converging prematurely to suboptimal policies that satisfy only a narrow subset of human preferences. In this work, we identify and address this preference exploration problem through population-based methods. We demonstrate that maintaining a diverse population of agents enables more comprehensive exploration of the preference landscape compared to single-agent approaches. Crucially, this diversity improves reward model learning by generating preference queries with clearly distinguishable behaviors, a key factor in real-world scenarios where humans must easily differentiate between options to provide meaningful feedback. Our experiments reveal that current methods may fail by getting stuck in local optima, requiring excessive feedback, or degrading significantly when human evaluators make errors on similar trajectories, a realistic scenario often overlooked by methods relying on perfect oracle teachers. Our population-based approach demonstrates robust performance when teachers mislabel similar trajectory segments and shows significantly enhanced preference exploration capabilities,particularly in environments with complex reward landscapes.

Evaluating Interpretable Reinforcement Learning by Distilling Policies into Programs

There exist applications of reinforcement learning like medicine where policies need to be ''interpretable'' by humans. User studies have shown that some policy classes might be more interpretable than others. However, it is costly to conduct human studies of policy interpretability. Furthermore, there is no clear definition of policy interpretabiliy, i.e., no clear metrics for interpretability and thus claims depend on the chosen definition. We tackle the problem of empirically evaluating policies interpretability without humans. Despite this lack of clear definition, researchers agree on the notions of ''simulatability'': policy interpretability should relate to how humans understand policy actions given states. To advance research in interpretable reinforcement learning, we contribute a new methodology to evaluate policy interpretability. This new methodology relies on proxies for simulatability that we use to conduct a large-scale empirical evaluation of policy interpretability. We use imitation learning to compute baseline policies by distilling expert neural networks into small programs. We then show that using our methodology to evaluate the baselines interpretability leads to similar conclusions as user studies. We show that increasing interpretability does not necessarily reduce performances and can sometimes increase them. We also show that there is no policy class that better trades off interpretability and performance across tasks making it necessary for researcher to have methodologies for comparing policies interpretability.

Augmented Bayesian Policy Search

Deterministic policies are often preferred over stochastic ones when implemented on physical systems. They can prevent erratic and harmful behaviors while being easier to implement and interpret. However, in practice, exploration is largely performed by stochastic policies. First-order Bayesian Optimization (BO) methods offer a principled way of performing exploration using deterministic policies. This is done through a learned probabilistic model of the objective function and its gradient. Nonetheless, such approaches treat policy search as a black-box problem, and thus, neglect the reinforcement learning nature of the problem. In this work, we leverage the performance difference lemma to introduce a novel mean function for the probabilistic model. This results in augmenting BO methods with the action-value function. Hence, we call our method Augmented Bayesian Search~(ABS). Interestingly, this new mean function enhances the posterior gradient with the deterministic policy gradient, effectively bridging the gap between BO and policy gradient methods. The resulting algorithm combines the convenience of the direct policy search with the scalability of reinforcement learning. We validate ABS on high-dimensional locomotion problems and demonstrate competitive performance compared to existing direct policy search schemes.

Interpretable and Editable Programmatic Tree Policies for Reinforcement Learning

Deep reinforcement learning agents are prone to goal misalignments. The black-box nature of their policies hinders the detection and correction of such misalignments, and the trust necessary for real-world deployment. So far, solutions learning interpretable policies are inefficient or require many human priors. We propose INTERPRETER, a fast distillation method producing INTerpretable Editable tRee Programs for ReinforcEmenT lEaRning. We empirically demonstrate that INTERPRETER compact tree programs match oracles across a diverse set of sequential decision tasks and evaluate the impact of our design choices on interpretability and performances. We show that our policies can be interpreted and edited to correct misalignments on Atari games and to explain real farming strategies.

Limits of Actor-Critic Algorithms for Decision Tree Policies Learning in IBMDPs

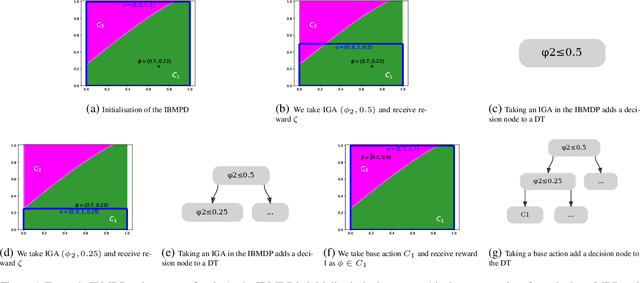
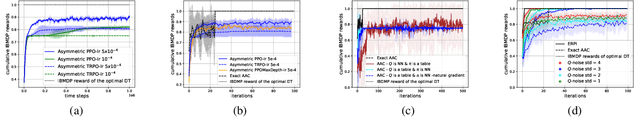
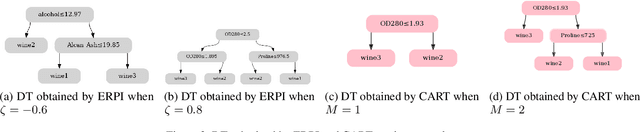
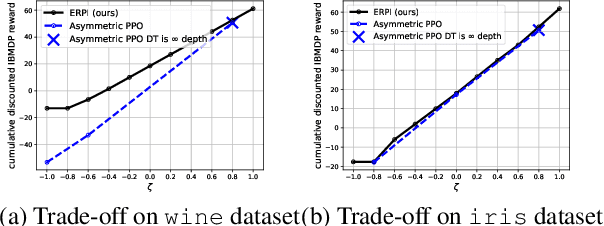
Interpretability of AI models allows for user safety checks to build trust in such AIs. In particular, Decision Trees (DTs) provide a global look at the learned model and transparently reveal which features of the input are critical for making a decision. However, interpretability is hindered if the DT is too large. To learn compact trees, a recent Reinforcement Learning (RL) framework has been proposed to explore the space of DTs using deep RL. This framework augments a decision problem (e.g. a supervised classification task) with additional actions that gather information about the features of an otherwise hidden input. By appropriately penalizing these actions, the agent learns to optimally trade-off size and performance of DTs. In practice, a reactive policy for a partially observable Markov decision process (MDP) needs to be learned, which is still an open problem. We show in this paper that deep RL can fail even on simple toy tasks of this class. However, when the underlying decision problem is a supervised classification task, we show that finding the optimal tree can be cast as a fully observable Markov decision problem and be solved efficiently, giving rise to a new family of algorithms for learning DTs that go beyond the classical greedy maximization ones.

Discovering the Interpretability-Performance Pareto Front of Decision Trees with Dynamic Programming

Decision trees are known to be intrinsically interpretable as they can be inspected and interpreted by humans. Furthermore, recent hardware advances have rekindled an interest for optimal decision tree algorithms, that produce more accurate trees than the usual greedy approaches. However, these optimal algorithms return a single tree optimizing a hand defined interpretability-performance trade-off, obtained by specifying a maximum number of decision nodes, giving no further insights about the quality of this trade-off. In this paper, we propose a new Markov Decision Problem (MDP) formulation for finding optimal decision trees. The main interest of this formulation is that we can compute the optimal decision trees for several interpretability-performance trade-offs by solving a single dynamic program, letting the user choose a posteriori the tree that best suits their needs. Empirically, we show that our method is competitive with state-of-the-art algorithms in terms of accuracy and runtime while returning a whole set of trees on the interpretability-performance Pareto front.

Optimal Interpretability-Performance Trade-off of Classification Trees with Black-Box Reinforcement Learning

Interpretability of AI models allows for user safety checks to build trust in these models. In particular, decision trees (DTs) provide a global view on the learned model and clearly outlines the role of the features that are critical to classify a given data. However, interpretability is hindered if the DT is too large. To learn compact trees, a Reinforcement Learning (RL) framework has been recently proposed to explore the space of DTs. A given supervised classification task is modeled as a Markov decision problem (MDP) and then augmented with additional actions that gather information about the features, equivalent to building a DT. By appropriately penalizing these actions, the RL agent learns to optimally trade-off size and performance of a DT. However, to do so, this RL agent has to solve a partially observable MDP. The main contribution of this paper is to prove that it is sufficient to solve a fully observable problem to learn a DT optimizing the interpretability-performance trade-off. As such any planning or RL algorithm can be used. We demonstrate the effectiveness of this approach on a set of classical supervised classification datasets and compare our approach with other interpretability-performance optimizing methods.

Entropy Regularized Reinforcement Learning with Cascading Networks

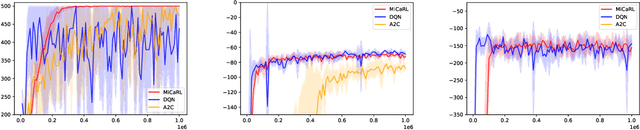
Deep Reinforcement Learning (Deep RL) has had incredible achievements on high dimensional problems, yet its learning process remains unstable even on the simplest tasks. Deep RL uses neural networks as function approximators. These neural models are largely inspired by developments in the (un)supervised machine learning community. Compared to these learning frameworks, one of the major difficulties of RL is the absence of i.i.d. data. One way to cope with this difficulty is to control the rate of change of the policy at every iteration. In this work, we challenge the common practices of the (un)supervised learning community of using a fixed neural architecture, by having a neural model that grows in size at each policy update. This allows a closed form entropy regularized policy update, which leads to a better control of the rate of change of the policy at each iteration and help cope with the non i.i.d. nature of RL. Initial experiments on classical RL benchmarks show promising results with remarkable convergence on some RL tasks when compared to other deep RL baselines, while exhibiting limitations on others.

Convex Optimization with an Interpolation-based Projection and its Application to Deep Learning

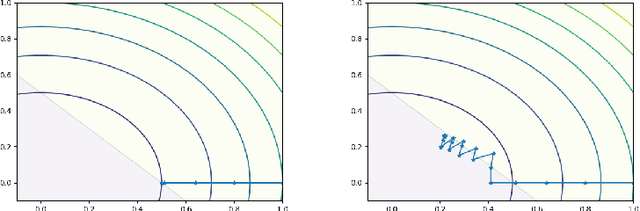
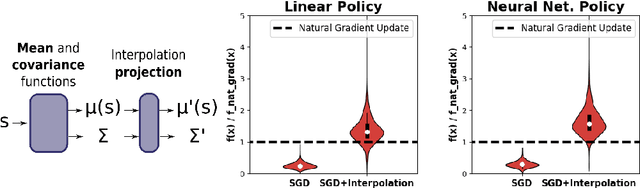
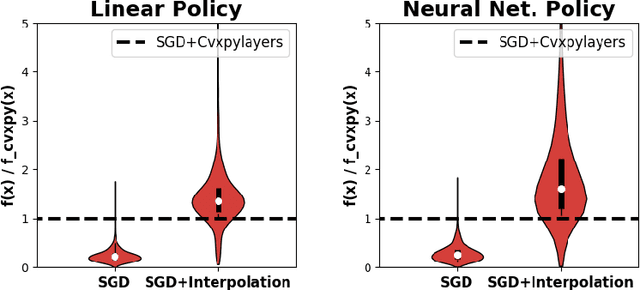
Convex optimizers have known many applications as differentiable layers within deep neural architectures. One application of these convex layers is to project points into a convex set. However, both forward and backward passes of these convex layers are significantly more expensive to compute than those of a typical neural network. We investigate in this paper whether an inexact, but cheaper projection, can drive a descent algorithm to an optimum. Specifically, we propose an interpolation-based projection that is computationally cheap and easy to compute given a convex, domain defining, function. We then propose an optimization algorithm that follows the gradient of the composition of the objective and the projection and prove its convergence for linear objectives and arbitrary convex and Lipschitz domain defining inequality constraints. In addition to the theoretical contributions, we demonstrate empirically the practical interest of the interpolation projection when used in conjunction with neural networks in a reinforcement learning and a supervised learning setting.

Reinforcement Learning from a Mixture of Interpretable Experts

Reinforcement learning (RL) has demonstrated its ability to solve high dimensional tasks by leveraging non-linear function approximators. These successes however are mostly achieved by 'black-box' policies in simulated domains. When deploying RL to the real world, several concerns regarding the use of a 'black-box' policy might be raised. In an effort to make the policies learned by RL more transparent, we propose in this paper a policy iteration scheme that retains a complex function approximator for its internal value predictions but constrains the policy to have a concise, hierarchical, and human-readable structure, based on a mixture of interpretable experts. We show that our proposed algorithm can learn compelling policies on continuous action deep RL benchmarks, matching the performance of neural network based policies, but returns policies that are more amenable to human inspection than neural network or linear-in-feature policies.