Riccardo Della Vecchia
BIDSA
AdaStop: sequential testing for efficient and reliable comparisons of Deep RL Agents
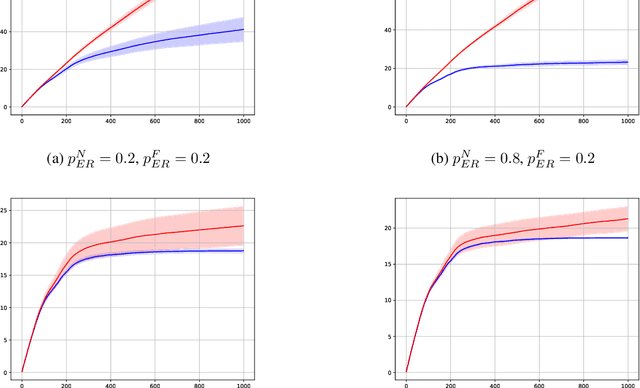
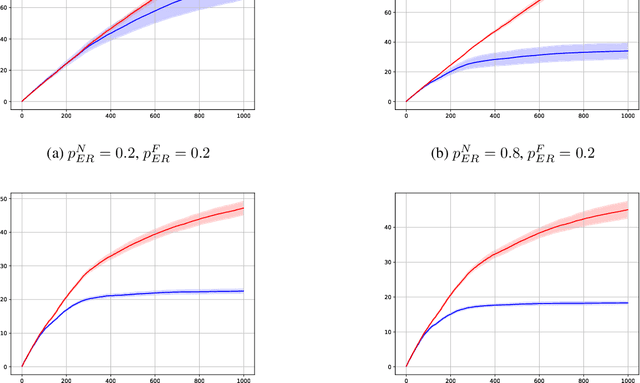
Jun 19, 2023Abstract:The reproducibility of many experimental results in Deep Reinforcement Learning (RL) is under question. To solve this reproducibility crisis, we propose a theoretically sound methodology to compare multiple Deep RL algorithms. The performance of one execution of a Deep RL algorithm is random so that independent executions are needed to assess it precisely. When comparing several RL algorithms, a major question is how many executions must be made and how can we assure that the results of such a comparison is theoretically sound. Researchers in Deep RL often use less than 5 independent executions to compare algorithms: we claim that this is not enough in general. Moreover, when comparing several algorithms at once, the error of each comparison accumulates and must be taken into account with a multiple tests procedure to preserve low error guarantees. To address this problem in a statistically sound way, we introduce AdaStop, a new statistical test based on multiple group sequential tests. When comparing algorithms, AdaStop adapts the number of executions to stop as early as possible while ensuring that we have enough information to distinguish algorithms that perform better than the others in a statistical significant way. We prove both theoretically and empirically that AdaStop has a low probability of making an error (Family-Wise Error). Finally, we illustrate the effectiveness of AdaStop in multiple use-cases, including toy examples and difficult cases such as Mujoco environments.
Online Instrumental Variable Regression: Regret Analysis and Bandit Feedback
Feb 18, 2023Abstract:The independence of noise and covariates is a standard assumption in online linear regression and linear bandit literature. This assumption and the following analysis are invalid in the case of endogeneity, i.e., when the noise and covariates are correlated. In this paper, we study the online setting of instrumental variable (IV) regression, which is widely used in economics to tackle endogeneity. Specifically, we analyse and upper bound regret of Two-Stage Least Squares (2SLS) approach to IV regression in the online setting. Our analysis shows that Online 2SLS (O2SLS) achieves $O(d^2 \log^2 T)$ regret after $T$ interactions, where d is the dimension of covariates. Following that, we leverage the O2SLS as an oracle to design OFUL-IV, a linear bandit algorithm. OFUL-IV can tackle endogeneity and achieves $O(d \sqrt{T} \log T)$ regret. For datasets with endogeneity, we experimentally demonstrate that O2SLS and OFUL-IV incur lower regrets than the state-of-the-art algorithms for both the online linear regression and linear bandit settings.
Entropy Regularized Reinforcement Learning with Cascading Networks
Oct 16, 2022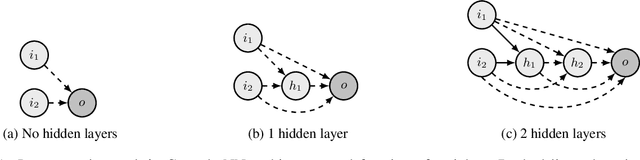
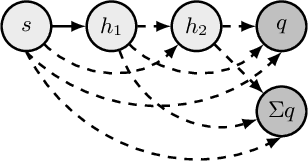
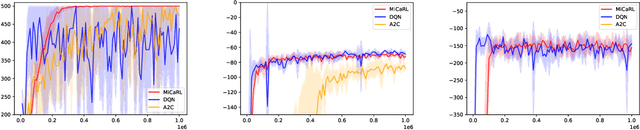

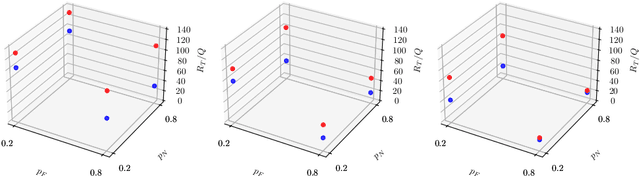
Abstract:Deep Reinforcement Learning (Deep RL) has had incredible achievements on high dimensional problems, yet its learning process remains unstable even on the simplest tasks. Deep RL uses neural networks as function approximators. These neural models are largely inspired by developments in the (un)supervised machine learning community. Compared to these learning frameworks, one of the major difficulties of RL is the absence of i.i.d. data. One way to cope with this difficulty is to control the rate of change of the policy at every iteration. In this work, we challenge the common practices of the (un)supervised learning community of using a fixed neural architecture, by having a neural model that grows in size at each policy update. This allows a closed form entropy regularized policy update, which leads to a better control of the rate of change of the policy at each iteration and help cope with the non i.i.d. nature of RL. Initial experiments on classical RL benchmarks show promising results with remarkable convergence on some RL tasks when compared to other deep RL baselines, while exhibiting limitations on others.
Cooperative Online Learning
Jun 09, 2021
Abstract:In this preliminary (and unpolished) version of the paper, we study an asynchronous online learning setting with a network of agents. At each time step, some of the agents are activated, requested to make a prediction, and pay the corresponding loss. Some feedback is then revealed to these agents and is later propagated through the network. We consider the case of full, bandit, and semi-bandit feedback. In particular, we construct a reduction to delayed single-agent learning that applies to both the full and the bandit feedback case and allows to obtain regret guarantees for both settings. We complement these results with a near-matching lower bound.
An Efficient Algorithm for Cooperative Semi-Bandits
Oct 05, 2020Abstract:We consider the problem of asynchronous online combinatorial optimization on a network of communicating agents. At each time step, some of the agents are stochastically activated, requested to make a prediction, and the system pays the corresponding loss. Then, neighbors of active agents receive semi-bandit feedback and exchange some succinct local information. The goal is to minimize the network regret, defined as the difference between the cumulative loss of the predictions of active agents and that of the best action in hindsight, selected from a combinatorial decision set. The main challenge in such a context is to control the computational complexity of the resulting algorithm while retaining minimax optimal regret guarantees. We introduce Coop-FTPL, a cooperative version of the well-known Follow The Perturbed Leader algorithm, that implements a new loss estimation procedure generalizing the Geometric Resampling of Neu and Bart\'ok [2013] to our setting. Assuming that the elements of the decision set are $k$-dimensional binary vectors with at most $m$ non-zero entries and $\alpha_1$ is the independence number of the network, we show that the expected regret of our algorithm after $T$ time steps is of order $Q\sqrt{mkT\log(k) (k\alpha_1/Q+m)}$, where $Q$ is the total activation probability mass. Furthermore, we prove that this is only $\sqrt{k\log k}$-away from the best achievable rate and that \coopftpl{} has a state-of-the-art $T^{3/2}$ worst-case computational complexity.
Clustering of solutions in the symmetric binary perceptron
Nov 18, 2019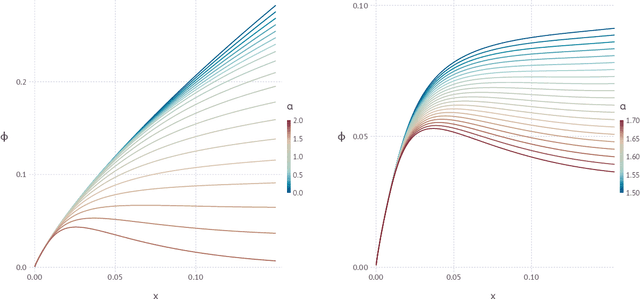
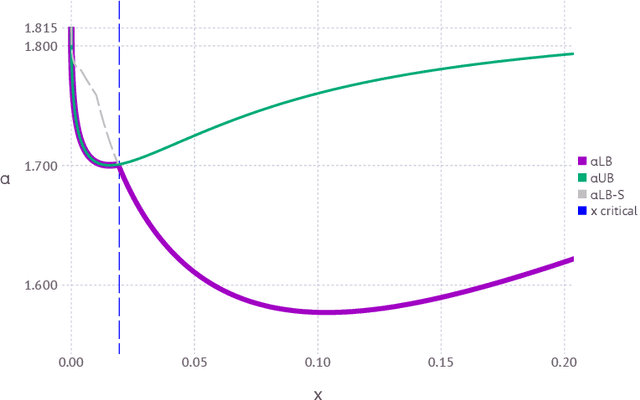
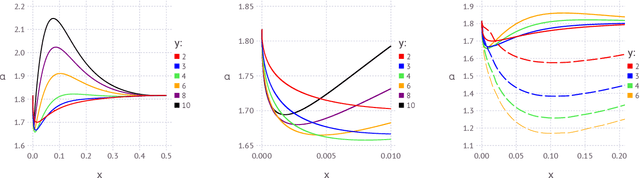
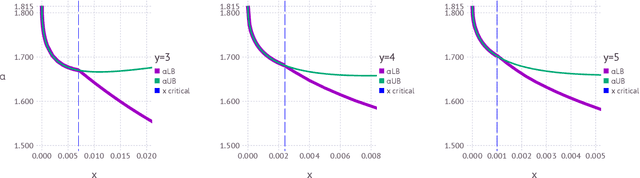
Abstract:The geometrical features of the (non-convex) loss landscape of neural network models are crucial in ensuring successful optimization and, most importantly, the capability to generalize well. While minimizers' flatness consistently correlates with good generalization, there has been little rigorous work in exploring the condition of existence of such minimizers, even in toy models. Here we consider a simple neural network model, the symmetric perceptron, with binary weights. Phrasing the learning problem as a constraint satisfaction problem, the analogous of a flat minimizer becomes a large and dense cluster of solutions, while the narrowest minimizers are isolated solutions. We perform the first steps toward the rigorous proof of the existence of a dense cluster in certain regimes of the parameters, by computing the first and second moment upper bounds for the existence of pairs of arbitrarily close solutions. Moreover, we present a non rigorous derivation of the same bounds for sets of $y$ solutions at fixed pairwise distances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge