Tommaso R. Cesari
Cooperative Online Learning
Jun 09, 2021
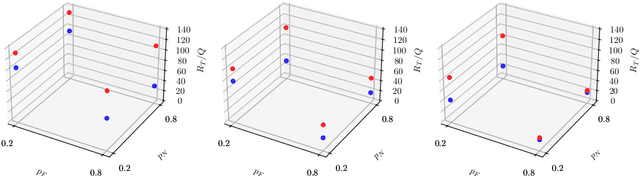
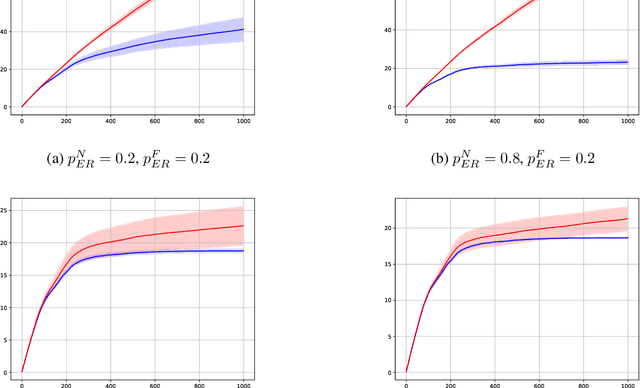
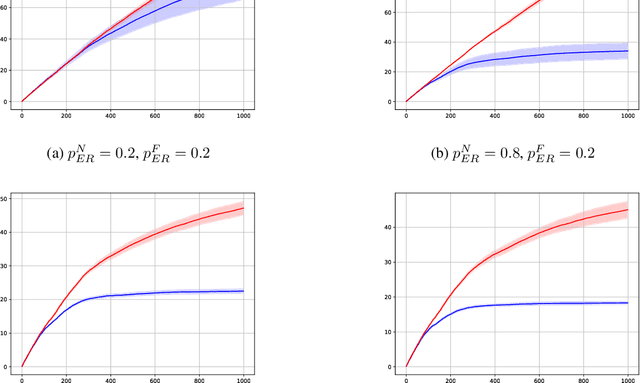
Abstract:In this preliminary (and unpolished) version of the paper, we study an asynchronous online learning setting with a network of agents. At each time step, some of the agents are activated, requested to make a prediction, and pay the corresponding loss. Some feedback is then revealed to these agents and is later propagated through the network. We consider the case of full, bandit, and semi-bandit feedback. In particular, we construct a reduction to delayed single-agent learning that applies to both the full and the bandit feedback case and allows to obtain regret guarantees for both settings. We complement these results with a near-matching lower bound.
Repeated A/B Testing
May 28, 2019Abstract:We study a setting in which a learner faces a sequence of A/B tests and has to make as many good decisions as possible within a given amount of time. Each A/B test $n$ is associated with an unknown (and potentially negative) reward $\mu_n \in [-1,1]$, drawn i.i.d. from an unknown and fixed distribution. For each A/B test $n$, the learner sequentially draws i.i.d. samples of a $\{-1,1\}$-valued random variable with mean $\mu_n$ until a halting criterion is met. The learner then decides to either accept the reward $\mu_n$ or to reject it and get zero instead. We measure the learner's performance as the sum of the expected rewards of the accepted $\mu_n$ divided by the total expected number of used time steps (which is different from the expected ratio between the total reward and the total number of used time steps). We design an algorithm and prove a data-dependent regret bound against any set of policies based on an arbitrary halting criterion and decision rule. Though our algorithm borrows ideas from multiarmed bandits, the two settings are significantly different and not directly comparable. In fact, the value of $\mu_n$ is never observed directly in our setting---unlike rewards in stochastic bandits. Moreover, the particular structure of our problem allows our regret bounds to be independent of the number of policies.
Cooperative Online Learning: Keeping your Neighbors Updated
Jan 23, 2019Abstract:We study an asynchronous online learning setting with a network of agents. At each time step, some of the agents are activated, requested to make a prediction, and pay the corresponding loss. The loss function is then revealed to these agents and also to their neighbors in the network. When activations are stochastic, we show that the regret achieved by $N$ agents running the standard online Mirror Descent is $O(\sqrt{\alpha T})$, where $T$ is the horizon and $\alpha \le N$ is the independence number of the network. This is in contrast to the regret $\Omega(\sqrt{N T})$ which $N$ agents incur in the same setting when feedback is not shared. We also show a matching lower bound of order $\sqrt{\alpha T}$ that holds for any given network. When the pattern of agent activations is arbitrary, the problem changes significantly: we prove a $\Omega(T)$ lower bound on the regret that holds for any online algorithm oblivious to the feedback source.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge