Autonomous Option Invention for Continual Hierarchical Reinforcement Learning and Planning

Abstraction is key to scaling up reinforcement learning (RL). However, autonomously learning abstract state and action representations to enable transfer and generalization remains a challenging open problem. This paper presents a novel approach for inventing, representing, and utilizing options, which represent temporally extended behaviors, in continual RL settings. Our approach addresses streams of stochastic problems characterized by long horizons, sparse rewards, and unknown transition and reward functions. Our approach continually learns and maintains an interpretable state abstraction, and uses it to invent high-level options with abstract symbolic representations. These options meet three key desiderata: (1) composability for solving tasks effectively with lookahead planning, (2) reusability across problem instances for minimizing the need for relearning, and (3) mutual independence for reducing interference among options. Our main contributions are approaches for continually learning transferable, generalizable options with symbolic representations, and for integrating search techniques with RL to efficiently plan over these learned options to solve new problems. Empirical results demonstrate that the resulting approach effectively learns and transfers abstract knowledge across problem instances, achieving superior sample efficiency compared to state-of-the-art methods.

Using Explainable AI and Hierarchical Planning for Outreach with Robots

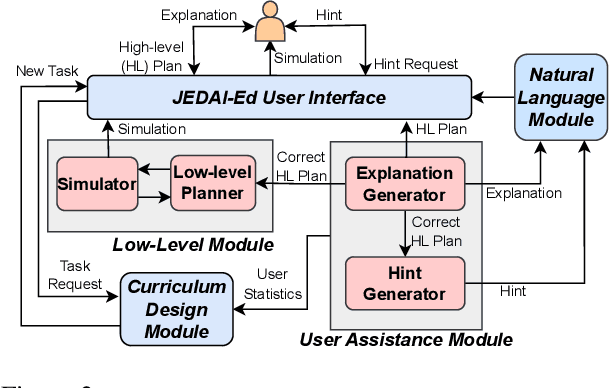
Understanding how robots plan and execute tasks is crucial in today's world, where they are becoming more prevalent in our daily lives. However, teaching non-experts the complexities of robot planning can be challenging. This work presents an open-source platform that simplifies the process using a visual interface that completely abstracts the complex internals of hierarchical planning that robots use for performing task and motion planning. Using the principles developed in the field of explainable AI, this intuitive platform enables users to create plans for robots to complete tasks, and provides helpful hints and natural language explanations for errors. The platform also has a built-in simulator to demonstrate how robots execute submitted plans. This platform's efficacy was tested in a user study on university students with little to no computer science background. Our results show that this platform is highly effective in teaching novice users the intuitions of robot task planning.

Learning Dynamic Abstract Representations for Sample-Efficient Reinforcement Learning

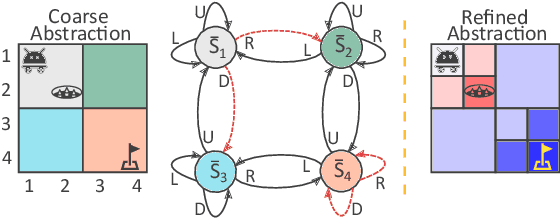
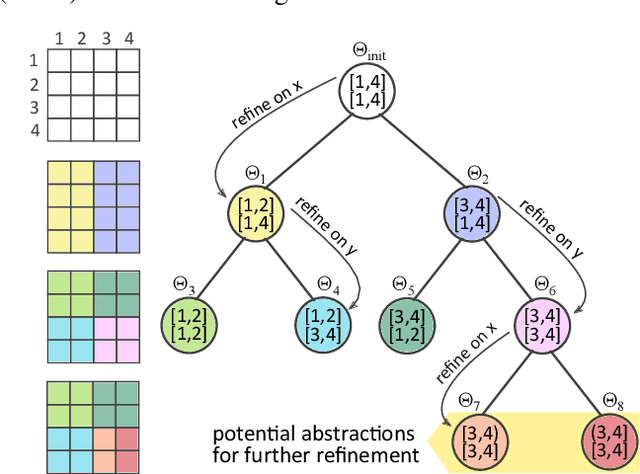
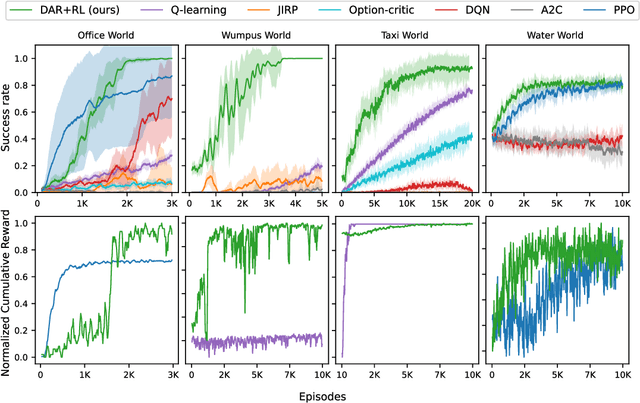
In many real-world problems, the learning agent needs to learn a problem's abstractions and solution simultaneously. However, most such abstractions need to be designed and refined by hand for different problems and domains of application. This paper presents a novel top-down approach for constructing state abstractions while carrying out reinforcement learning. Starting with state variables and a simulator, it presents a novel domain-independent approach for dynamically computing an abstraction based on the dispersion of Q-values in abstract states as the agent continues acting and learning. Extensive empirical evaluation on multiple domains and problems shows that this approach automatically learns abstractions that are finely-tuned to the problem, yield powerful sample efficiency, and result in the RL agent significantly outperforming existing approaches.

Preliminary Results on Using Abstract AND-OR Graphs for Generalized Solving of Stochastic Shortest Path Problems

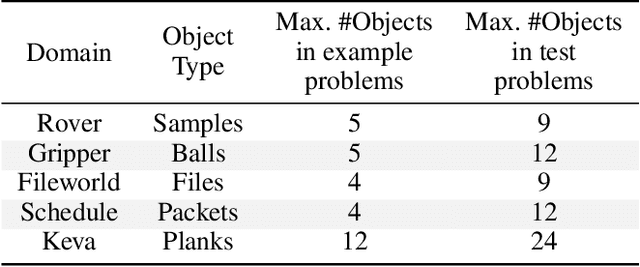
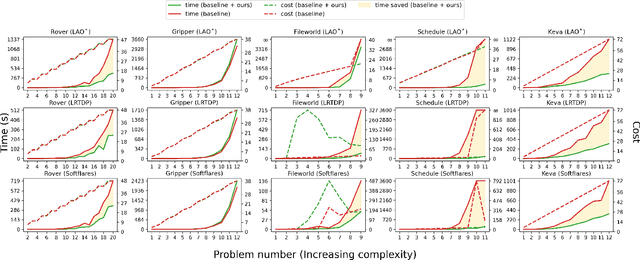
Several goal-oriented problems in the real-world can be naturally expressed as Stochastic Shortest Path Problems (SSPs). However, a key difficulty for computing solutions for problems in the SSP framework is that the computational requirements often make finding solutions to even moderately sized problems intractable. Solutions to many of such problems can often be expressed as generalized policies that are quite easy to compute from small examples and are readily applicable to problems with a larger number of objects and/or different object names. In this paper, we provide a preliminary study on using canonical abstractions to compute such generalized policies and represent them as AND-OR graphs that translate to simple non-deterministic, memoryless controllers. Such policy structures naturally lend themselves to a hierarchical approach for solving problems and we show that our approach can be embedded in any SSP solver to compute hierarchically optimal policies. We conducted an empirical evaluation on some well-known planning benchmarks and difficult robotics domains and show that our approach is promising, often computing optimal policies significantly faster than state-of-art SSP solvers.

Differential Assessment of Black-Box AI Agents

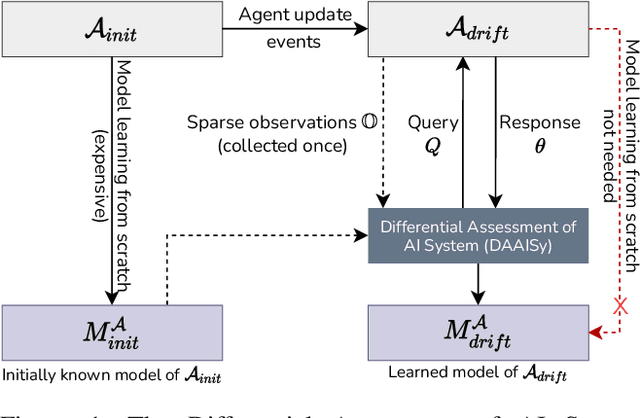
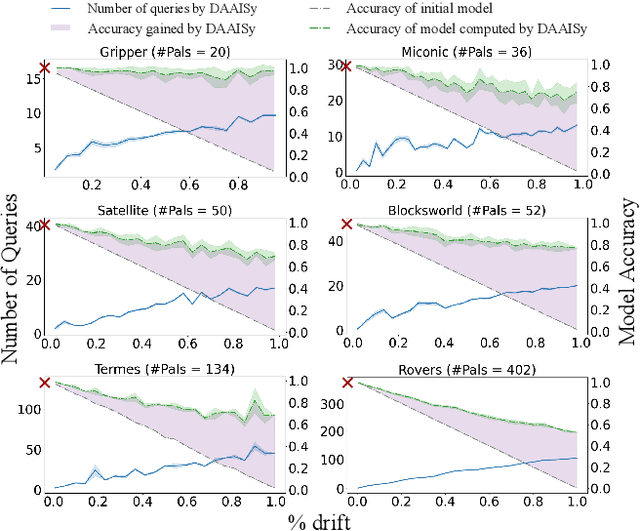
Much of the research on learning symbolic models of AI agents focuses on agents with stationary models. This assumption fails to hold in settings where the agent's capabilities may change as a result of learning, adaptation, or other post-deployment modifications. Efficient assessment of agents in such settings is critical for learning the true capabilities of an AI system and for ensuring its safe usage. In this work, we propose a novel approach to differentially assess black-box AI agents that have drifted from their previously known models. As a starting point, we consider the fully observable and deterministic setting. We leverage sparse observations of the drifted agent's current behavior and knowledge of its initial model to generate an active querying policy that selectively queries the agent and computes an updated model of its functionality. Empirical evaluation shows that our approach is much more efficient than re-learning the agent model from scratch. We also show that the cost of differential assessment using our method is proportional to the amount of drift in the agent's functionality.