Preliminary Results on Using Abstract AND-OR Graphs for Generalized Solving of Stochastic Shortest Path Problems

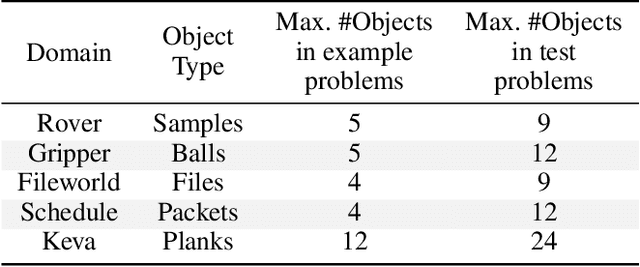
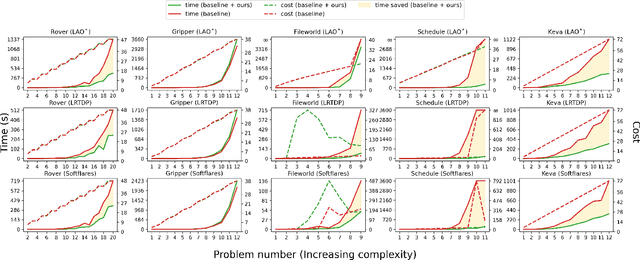
Several goal-oriented problems in the real-world can be naturally expressed as Stochastic Shortest Path Problems (SSPs). However, a key difficulty for computing solutions for problems in the SSP framework is that the computational requirements often make finding solutions to even moderately sized problems intractable. Solutions to many of such problems can often be expressed as generalized policies that are quite easy to compute from small examples and are readily applicable to problems with a larger number of objects and/or different object names. In this paper, we provide a preliminary study on using canonical abstractions to compute such generalized policies and represent them as AND-OR graphs that translate to simple non-deterministic, memoryless controllers. Such policy structures naturally lend themselves to a hierarchical approach for solving problems and we show that our approach can be embedded in any SSP solver to compute hierarchically optimal policies. We conducted an empirical evaluation on some well-known planning benchmarks and difficult robotics domains and show that our approach is promising, often computing optimal policies significantly faster than state-of-art SSP solvers.