GUTS: Generalized Uncertainty-Aware Thompson Sampling for Multi-Agent Active Search

Robotic solutions for quick disaster response are essential to ensure minimal loss of life, especially when the search area is too dangerous or too vast for human rescuers. We model this problem as an asynchronous multi-agent active-search task where each robot aims to efficiently seek objects of interest (OOIs) in an unknown environment. This formulation addresses the requirement that search missions should focus on quick recovery of OOIs rather than full coverage of the search region. Previous approaches fail to accurately model sensing uncertainty, account for occlusions due to foliage or terrain, or consider the requirement for heterogeneous search teams and robustness to hardware and communication failures. We present the Generalized Uncertainty-aware Thompson Sampling (GUTS) algorithm, which addresses these issues and is suitable for deployment on heterogeneous multi-robot systems for active search in large unstructured environments. We show through simulation experiments that GUTS consistently outperforms existing methods such as parallelized Thompson Sampling and exhaustive search, recovering all OOIs in 80% of all runs. In contrast, existing approaches recover all OOIs in less than 40% of all runs. We conduct field tests using our multi-robot system in an unstructured environment with a search area of approximately 75,000 sq. m. Our system demonstrates robustness to various failure modes, achieving full recovery of OOIs (where feasible) in every field run, and significantly outperforming our baseline.

Cost Aware Asynchronous Multi-Agent Active Search

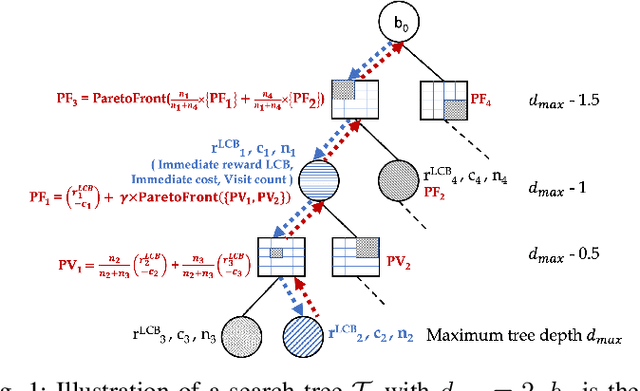
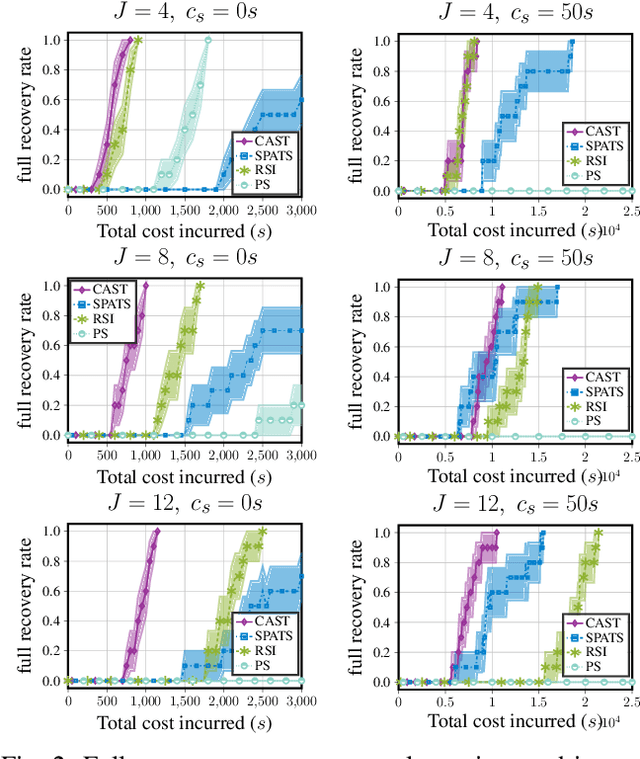
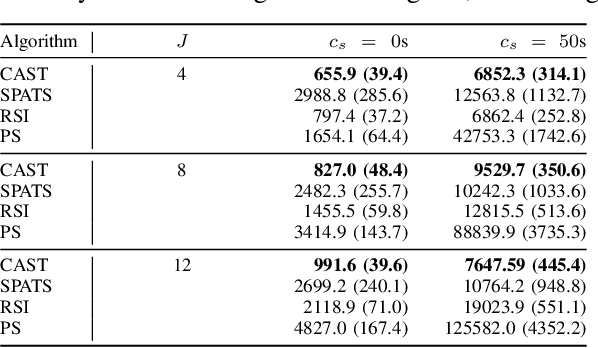
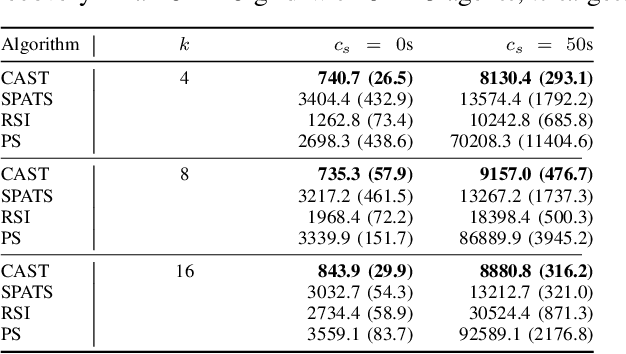
Multi-agent active search requires autonomous agents to choose sensing actions that efficiently locate targets. In a realistic setting, agents also must consider the costs that their decisions incur. Previously proposed active search algorithms simplify the problem by ignoring uncertainty in the agent's environment, using myopic decision making, and/or overlooking costs. In this paper, we introduce an online active search algorithm to detect targets in an unknown environment by making adaptive cost-aware decisions regarding the agent's actions. Our algorithm combines principles from Thompson Sampling (for search space exploration and decentralized multi-agent decision making), Monte Carlo Tree Search (for long horizon planning) and pareto-optimal confidence bounds (for multi-objective optimization in an unknown environment) to propose an online lookahead planner that removes all the simplifications. We analyze the algorithm's performance in simulation to show its efficacy in cost aware active search.

Multi-Agent Active Search using Detection and Location Uncertainty

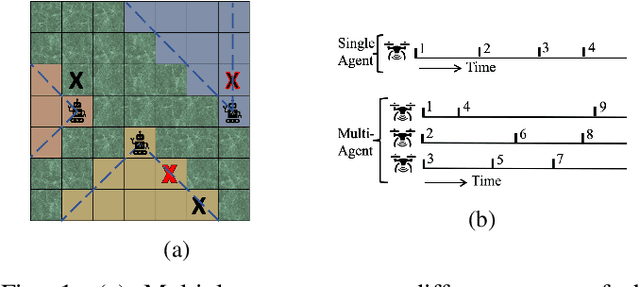
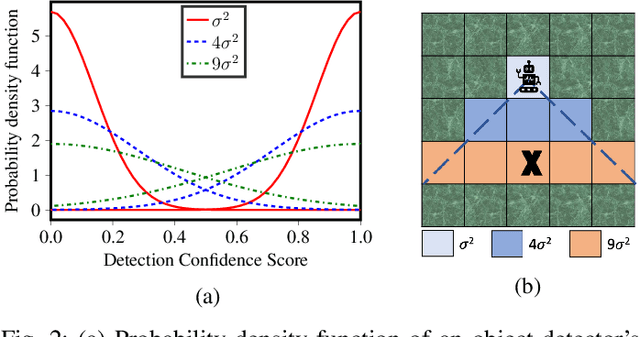
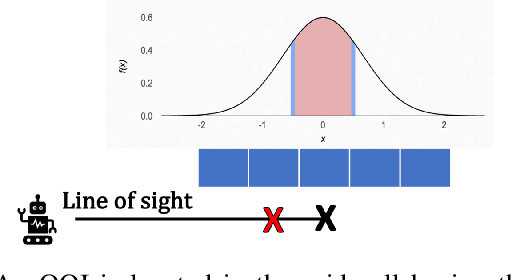
Active search refers to the task of autonomous robots (agents) detecting objects of interest (targets) in a search space using decision making algorithms that adapt to the history of their observations. It has important applications in search and rescue missions, wildlife patrolling and environment monitoring. Active search algorithms must contend with two types of uncertainty: detection uncertainty and location uncertainty. Prior work has typically focused on one of these while ignoring or engineering away the other. The more common approach in robotics is to focus on location uncertainty and remove detection uncertainty by thresholding the detection probability to zero or one. On the other hand, it is common in the sparse signal processing literature to assume the target location is accurate and focus on the uncertainty of its detection. In this work, we propose an inference method to jointly handle both target detection and location uncertainty. We then build a decision making algorithm on this inference method that uses Thompson sampling to enable efficient active search in both the single agent and multi-agent settings. We perform experiments in simulation over varying number of agents and targets to show that our inference and decision making algorithms outperform competing baselines that only account for either target detection or location uncertainty.

Multi-Agent Active Search using Realistic Depth-Aware Noise Model

The search for objects of interest in an unknown environment by making data-collection decisions (i.e., active search or active sensing) has robotics applications in many fields, including the search and rescue of human survivors following disasters, detecting gas leaks or locating and preventing animal poachers. Existing algorithms often prioritize the location accuracy of objects of interest while other practical issues such as the reliability of object detection as a function of distance and lines of sight remain largely ignored. An additional challenge is that in many active search scenarios, communication infrastructure may be damaged, unreliable, or unestablished, making centralized control of multiple search agents impractical. We present an algorithm called Noise-Aware Thompson Sampling (NATS) that addresses these issues for multiple ground-based robot agents performing active search considering two sources of sensory information from monocular optical imagery and sonar tracking. NATS utilizes communications between robot agents in a decentralized manner that is robust to intermittent loss of communication links. Additionally, it takes into account object detection uncertainty from depth as well as environmental occlusions. Using simulation results, we show that NATS significantly outperforms existing methods such as information-greedy policies or exhaustive search. We demonstrate the real-world viability of NATS using a photo-realistic environment created in the Unreal Engine 4 game development platform with the AirSim plugin.

Asynchronous Multi Agent Active Search

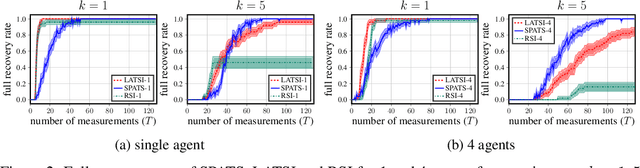
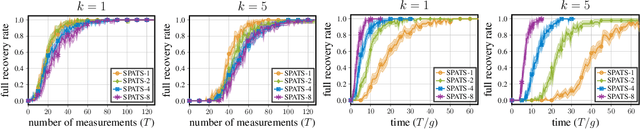
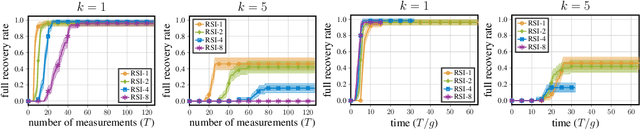
Active search refers to the problem of efficiently locating targets in an unknown environment by actively making data-collection decisions, and has many applications including detecting gas leaks, radiation sources or human survivors of disasters using aerial and/or ground robots (agents). Existing active search methods are in general only amenable to a single agent, or if they extend to multi agent they require a central control system to coordinate the actions of all agents. However, such control systems are often impractical in robotics applications. In this paper, we propose two distinct active search algorithms called SPATS (Sparse Parallel Asynchronous Thompson Sampling) and LATSI (LAplace Thompson Sampling with Information gain) that allow for multiple agents to independently make data-collection decisions without a central coordinator. Throughout we consider that targets are sparsely located around the environment in keeping with compressive sensing assumptions and its applicability in real world scenarios. Additionally, while most common search algorithms assume that agents can sense the entire environment (e.g. compressive sensing) or sense point-wise (e.g. Bayesian Optimization) at all times, we make a realistic assumption that each agent can only sense a contiguous region of space at a time. We provide simulation results as well as theoretical analysis to demonstrate the efficacy of our proposed algorithms.

MSE-Optimal Neural Network Initialization via Layer Fusion

Deep neural networks achieve state-of-the-art performance for a range of classification and inference tasks. However, the use of stochastic gradient descent combined with the nonconvexity of the underlying optimization problems renders parameter learning susceptible to initialization. To address this issue, a variety of methods that rely on random parameter initialization or knowledge distillation have been proposed in the past. In this paper, we propose FuseInit, a novel method to initialize shallower networks by fusing neighboring layers of deeper networks that are trained with random initialization. We develop theoretical results and efficient algorithms for mean-square error (MSE)-optimal fusion of neighboring dense-dense, convolutional-dense, and convolutional-convolutional layers. We show experiments for a range of classification and regression datasets, which suggest that deeper neural networks are less sensitive to initialization and shallower networks can perform better (sometimes as well as their deeper counterparts) if initialized with FuseInit.

Linear Spectral Estimators and an Application to Phase Retrieval

Phase retrieval refers to the problem of recovering real- or complex-valued vectors from magnitude measurements. The best-known algorithms for this problem are iterative in nature and rely on so-called spectral initializers that provide accurate initialization vectors. We propose a novel class of estimators suitable for general nonlinear measurement systems, called linear spectral estimators (LSPEs), which can be used to compute accurate initialization vectors for phase retrieval problems. The proposed LSPEs not only provide accurate initialization vectors for noisy phase retrieval systems with structured or random measurement matrices, but also enable the derivation of sharp and nonasymptotic mean-squared error bounds. We demonstrate the efficacy of LSPEs on synthetic and real-world phase retrieval problems, and show that our estimators significantly outperform existing methods for structured measurement systems that arise in practice.