Exactly Computing do-Shapley Values

Structural Causal Models (SCM) are a powerful framework for describing complicated dynamics across the natural sciences. A particularly elegant way of interpreting SCMs is do-Shapley, a game-theoretic method of quantifying the average effect of $d$ variables across exponentially many interventions. Like Shapley values, computing do-Shapley values generally requires evaluating exponentially many terms. The foundation of our work is a reformulation of do-Shapley values in terms of the irreducible sets of the underlying SCM. Leveraging this insight, we can exactly compute do-Shapley values in time linear in the number of irreducible sets $r$, which itself can range from $d$ to $2^d$ depending on the graph structure of the SCM. Since $r$ is unknown a priori, we complement the exact algorithm with an estimator that, like general Shapley value estimators, can be run with any query budget. As the query budget approaches $r$, our estimators can produce more accurate estimates than prior methods by several orders of magnitude, and, when the budget reaches $r$, return the Shapley values up to machine precision. Beyond computational speed, we also reduce the identification burden: we prove that non-parametric identifiability of do-Shapley values requires only the identification of interventional effects for the $d$ singleton coalitions, rather than all classes.

An Odd Estimator for Shapley Values

The Shapley value is a ubiquitous framework for attribution in machine learning, encompassing feature importance, data valuation, and causal inference. However, its exact computation is generally intractable, necessitating efficient approximation methods. While the most effective and popular estimators leverage the paired sampling heuristic to reduce estimation error, the theoretical mechanism driving this improvement has remained opaque. In this work, we provide an elegant and fundamental justification for paired sampling: we prove that the Shapley value depends exclusively on the odd component of the set function, and that paired sampling orthogonalizes the regression objective to filter out the irrelevant even component. Leveraging this insight, we propose OddSHAP, a novel consistent estimator that performs polynomial regression solely on the odd subspace. By utilizing the Fourier basis to isolate this subspace and employing a proxy model to identify high-impact interactions, OddSHAP overcomes the combinatorial explosion of higher-order approximations. Through an extensive benchmark evaluation, we find that OddSHAP achieves state-of-the-art estimation accuracy.

PolySHAP: Extending KernelSHAP with Interaction-Informed Polynomial Regression

Shapley values have emerged as a central game-theoretic tool in explainable AI (XAI). However, computing Shapley values exactly requires $2^d$ game evaluations for a model with $d$ features. Lundberg and Lee's KernelSHAP algorithm has emerged as a leading method for avoiding this exponential cost. KernelSHAP approximates Shapley values by approximating the game as a linear function, which is fit using a small number of game evaluations for random feature subsets. In this work, we extend KernelSHAP by approximating the game via higher degree polynomials, which capture non-linear interactions between features. Our resulting PolySHAP method yields empirically better Shapley value estimates for various benchmark datasets, and we prove that these estimates are consistent. Moreover, we connect our approach to paired sampling (antithetic sampling), a ubiquitous modification to KernelSHAP that improves empirical accuracy. We prove that paired sampling outputs exactly the same Shapley value approximations as second-order PolySHAP, without ever fitting a degree 2 polynomial. To the best of our knowledge, this finding provides the first strong theoretical justification for the excellent practical performance of the paired sampling heuristic.

Regression-adjusted Monte Carlo Estimators for Shapley Values and Probabilistic Values

With origins in game theory, probabilistic values like Shapley values, Banzhaf values, and semi-values have emerged as a central tool in explainable AI. They are used for feature attribution, data attribution, data valuation, and more. Since all of these values require exponential time to compute exactly, research has focused on efficient approximation methods using two techniques: Monte Carlo sampling and linear regression formulations. In this work, we present a new way of combining both of these techniques. Our approach is more flexible than prior algorithms, allowing for linear regression to be replaced with any function family whose probabilistic values can be computed efficiently. This allows us to harness the accuracy of tree-based models like XGBoost, while still producing unbiased estimates. From experiments across eight datasets, we find that our methods give state-of-the-art performance for estimating probabilistic values. For Shapley values, the error of our methods can be $6.5\times$ lower than Permutation SHAP (the most popular Monte Carlo method), $3.8\times$ lower than Kernel SHAP (the most popular linear regression method), and $2.6\times$ lower than Leverage SHAP (the prior state-of-the-art Shapley value estimator). For more general probabilistic values, we can obtain error $215\times$ lower than the best estimator from prior work.

SEAL: Semantic Aware Image Watermarking

Generative models have rapidly evolved to generate realistic outputs. However, their synthetic outputs increasingly challenge the clear distinction between natural and AI-generated content, necessitating robust watermarking techniques. Watermarks are typically expected to preserve the integrity of the target image, withstand removal attempts, and prevent unauthorized replication onto unrelated images. To address this need, recent methods embed persistent watermarks into images produced by diffusion models using the initial noise. Yet, to do so, they either distort the distribution of generated images or rely on searching through a long dictionary of used keys for detection. In this paper, we propose a novel watermarking method that embeds semantic information about the generated image directly into the watermark, enabling a distortion-free watermark that can be verified without requiring a database of key patterns. Instead, the key pattern can be inferred from the semantic embedding of the image using locality-sensitive hashing. Furthermore, conditioning the watermark detection on the original image content improves robustness against forgery attacks. To demonstrate that, we consider two largely overlooked attack strategies: (i) an attacker extracting the initial noise and generating a novel image with the same pattern; (ii) an attacker inserting an unrelated (potentially harmful) object into a watermarked image, possibly while preserving the watermark. We empirically validate our method's increased robustness to these attacks. Taken together, our results suggest that content-aware watermarks can mitigate risks arising from image-generative models.

Hidden in the Noise: Two-Stage Robust Watermarking for Images

As the quality of image generators continues to improve, deepfakes become a topic of considerable societal debate. Image watermarking allows responsible model owners to detect and label their AI-generated content, which can mitigate the harm. Yet, current state-of-the-art methods in image watermarking remain vulnerable to forgery and removal attacks. This vulnerability occurs in part because watermarks distort the distribution of generated images, unintentionally revealing information about the watermarking techniques. In this work, we first demonstrate a distortion-free watermarking method for images, based on a diffusion model's initial noise. However, detecting the watermark requires comparing the initial noise reconstructed for an image to all previously used initial noises. To mitigate these issues, we propose a two-stage watermarking framework for efficient detection. During generation, we augment the initial noise with generated Fourier patterns to embed information about the group of initial noises we used. For detection, we (i) retrieve the relevant group of noises, and (ii) search within the given group for an initial noise that might match our image. This watermarking approach achieves state-of-the-art robustness to forgery and removal against a large battery of attacks.

Kernel Banzhaf: A Fast and Robust Estimator for Banzhaf Values

Banzhaf values offer a simple and interpretable alternative to the widely-used Shapley values. We introduce Kernel Banzhaf, a novel algorithm inspired by KernelSHAP, that leverages an elegant connection between Banzhaf values and linear regression. Through extensive experiments on feature attribution tasks, we demonstrate that Kernel Banzhaf substantially outperforms other algorithms for estimating Banzhaf values in both sample efficiency and robustness to noise. Furthermore, we prove theoretical guarantees on the algorithm's performance, establishing Kernel Banzhaf as a valuable tool for interpretable machine learning.

FairlyUncertain: A Comprehensive Benchmark of Uncertainty in Algorithmic Fairness

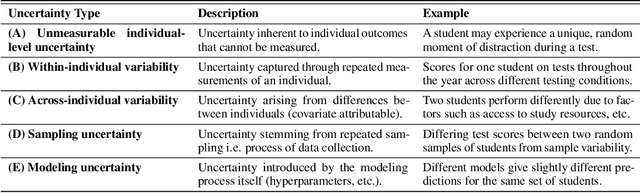
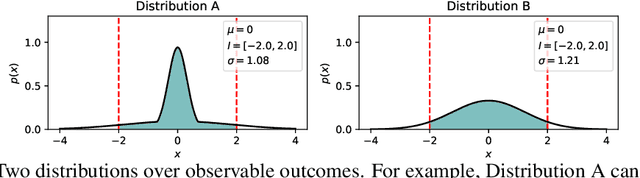
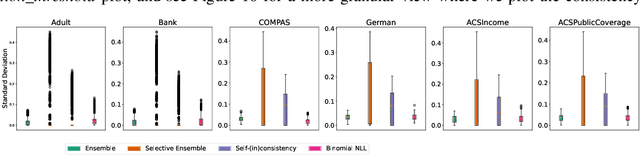
Fair predictive algorithms hinge on both equality and trust, yet inherent uncertainty in real-world data challenges our ability to make consistent, fair, and calibrated decisions. While fairly managing predictive error has been extensively explored, some recent work has begun to address the challenge of fairly accounting for irreducible prediction uncertainty. However, a clear taxonomy and well-specified objectives for integrating uncertainty into fairness remains undefined. We address this gap by introducing FairlyUncertain, an axiomatic benchmark for evaluating uncertainty estimates in fairness. Our benchmark posits that fair predictive uncertainty estimates should be consistent across learning pipelines and calibrated to observed randomness. Through extensive experiments on ten popular fairness datasets, our evaluation reveals: (1) A theoretically justified and simple method for estimating uncertainty in binary settings is more consistent and calibrated than prior work; (2) Abstaining from binary predictions, even with improved uncertainty estimates, reduces error but does not alleviate outcome imbalances between demographic groups; (3) Incorporating consistent and calibrated uncertainty estimates in regression tasks improves fairness without any explicit fairness interventions. Additionally, our benchmark package is designed to be extensible and open-source, to grow with the field. By providing a standardized framework for assessing the interplay between uncertainty and fairness, FairlyUncertain paves the way for more equitable and trustworthy machine learning practices.

Provably Accurate Shapley Value Estimation via Leverage Score Sampling

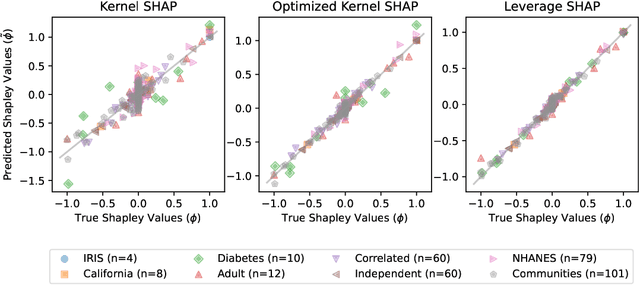
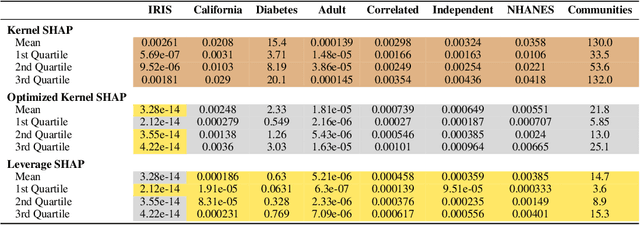
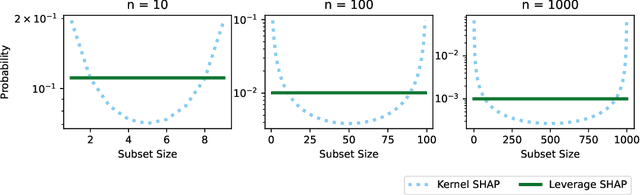
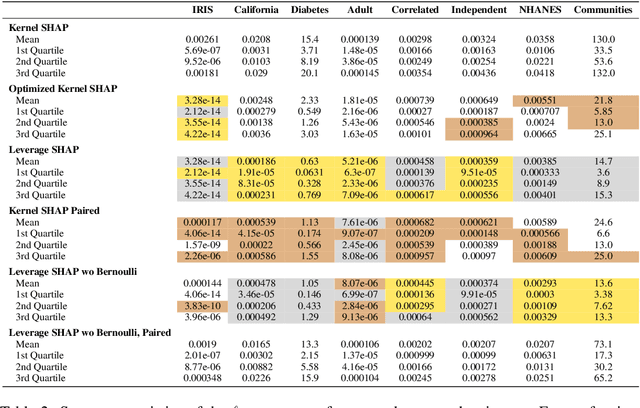
Originally introduced in game theory, Shapley values have emerged as a central tool in explainable machine learning, where they are used to attribute model predictions to specific input features. However, computing Shapley values exactly is expensive: for a general model with $n$ features, $O(2^n)$ model evaluations are necessary. To address this issue, approximation algorithms are widely used. One of the most popular is the Kernel SHAP algorithm, which is model agnostic and remarkably effective in practice. However, to the best of our knowledge, Kernel SHAP has no strong non-asymptotic complexity guarantees. We address this issue by introducing Leverage SHAP, a light-weight modification of Kernel SHAP that provides provably accurate Shapley value estimates with just $O(n\log n)$ model evaluations. Our approach takes advantage of a connection between Shapley value estimation and agnostic active learning by employing leverage score sampling, a powerful regression tool. Beyond theoretical guarantees, we show that Leverage SHAP consistently outperforms even the highly optimized implementation of Kernel SHAP available in the ubiquitous SHAP library [Lundberg & Lee, 2017].

Benchmarking Estimators for Natural Experiments: A Novel Dataset and a Doubly Robust Algorithm

Estimating the effect of treatments from natural experiments, where treatments are pre-assigned, is an important and well-studied problem. We introduce a novel natural experiment dataset obtained from an early childhood literacy nonprofit. Surprisingly, applying over 20 established estimators to the dataset produces inconsistent results in evaluating the nonprofit's efficacy. To address this, we create a benchmark to evaluate estimator accuracy using synthetic outcomes, whose design was guided by domain experts. The benchmark extensively explores performance as real world conditions like sample size, treatment correlation, and propensity score accuracy vary. Based on our benchmark, we observe that the class of doubly robust treatment effect estimators, which are based on simple and intuitive regression adjustment, generally outperform other more complicated estimators by orders of magnitude. To better support our theoretical understanding of doubly robust estimators, we derive a closed form expression for the variance of any such estimator that uses dataset splitting to obtain an unbiased estimate. This expression motivates the design of a new doubly robust estimator that uses a novel loss function when fitting functions for regression adjustment. We release the dataset and benchmark in a Python package; the package is built in a modular way to facilitate new datasets and estimators.