R. J. Cintra
A Note on the Conversion of Nonnegative Integers to the Canonical Signed-digit Representation
Jan 19, 2025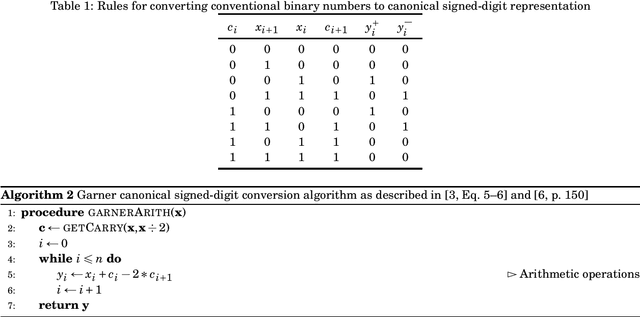
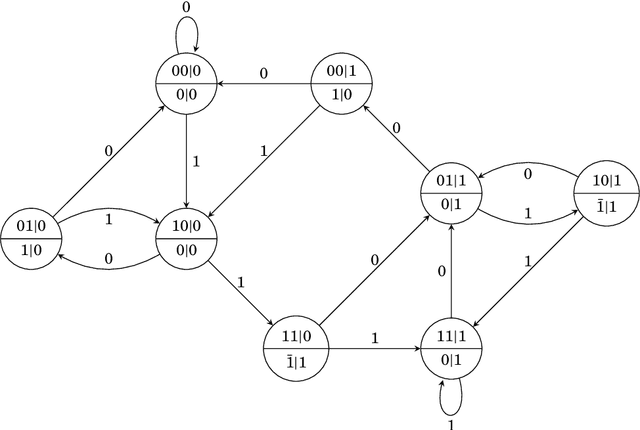
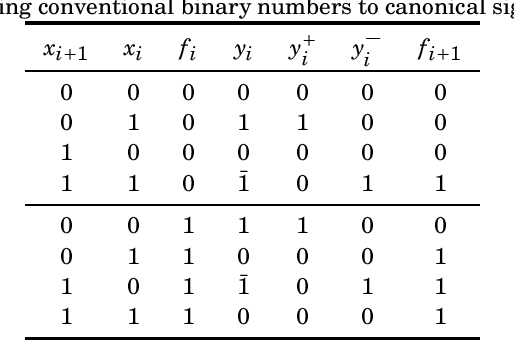
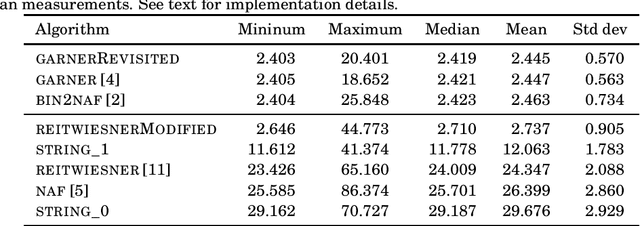
Abstract:This note addresses the signed-digit representation of non-negative integer binary numbers. We review and revisit popular literature methods for canonical signed-digit representation. A method based on string substitution is discussed.
Extensions on low-complexity DCT approximations for larger blocklengths based on minimal angle similarity
Oct 20, 2024Abstract:The discrete cosine transform (DCT) is a central tool for image and video coding because it can be related to the Karhunen-Lo\`eve transform (KLT), which is the optimal transform in terms of retained transform coefficients and data decorrelation. In this paper, we introduce 16-, 32-, and 64-point low-complexity DCT approximations by minimizing individually the angle between the rows of the exact DCT matrix and the matrix induced by the approximate transforms. According to some classical figures of merit, the proposed transforms outperformed the approximations for the DCT already known in the literature. Fast algorithms were also developed for the low-complexity transforms, asserting a good balance between the performance and its computational cost. Practical applications in image encoding showed the relevance of the transforms in this context. In fact, the experiments showed that the proposed transforms had better results than the known approximations in the literature for the cases of 16, 32, and 64 blocklength.
* Fixed typos. 27 pages, 6 figures, 5 tables
Regression Model for Speckled Data with Extremely Variability
Oct 14, 2024Abstract:Synthetic aperture radar (SAR) is an efficient and widely used remote sensing tool. However, data extracted from SAR images are contaminated with speckle, which precludes the application of techniques based on the assumption of additive and normally distributed noise. One of the most successful approaches to describing such data is the multiplicative model, where intensities can follow a variety of distributions with positive support. The $\mathcal{G}^0_I$ model is among the most successful ones. Although several estimation methods for the $\mathcal{G}^0_I$ parameters have been proposed, there is no work exploring a regression structure for this model. Such a structure could allow us to infer unobserved values from available ones. In this work, we propose a $\mathcal{G}^0_I$ regression model and use it to describe the influence of intensities from other polarimetric channels. We derive some theoretical properties for the new model: Fisher information matrix, residual measures, and influential tools. Maximum likelihood point and interval estimation methods are proposed and evaluated by Monte Carlo experiments. Results from simulated and actual data show that the new model can be helpful for SAR image analysis.
* 29 pages, 6 figures, 3 tables
Fast Data-independent KLT Approximations Based on Integer Functions
Oct 11, 2024Abstract:The Karhunen-Lo\`eve transform (KLT) stands as a well-established discrete transform, demonstrating optimal characteristics in data decorrelation and dimensionality reduction. Its ability to condense energy compression into a select few main components has rendered it instrumental in various applications within image compression frameworks. However, computing the KLT depends on the covariance matrix of the input data, which makes it difficult to develop fast algorithms for its implementation. Approximations for the KLT, utilizing specific rounding functions, have been introduced to reduce its computational complexity. Therefore, our paper introduces a category of low-complexity, data-independent KLT approximations, employing a range of round-off functions. The design methodology of the approximate transform is defined for any block-length $N$, but emphasis is given to transforms of $N = 8$ due to its wide use in image and video compression. The proposed transforms perform well when compared to the exact KLT and approximations considering classical performance measures. For particular scenarios, our proposed transforms demonstrated superior performance when compared to KLT approximations documented in the literature. We also developed fast algorithms for the proposed transforms, further reducing the arithmetic cost associated with their implementation. Evaluation of field programmable gate array (FPGA) hardware implementation metrics was conducted. Practical applications in image encoding showed the relevance of the proposed transforms. In fact, we showed that one of the proposed transforms outperformed the exact KLT given certain compression ratios.
* 19 pages, 10 figures, 7 tables
An Approximation for the 32-point Discrete Fourier Transform
Jul 17, 2024Abstract:This brief note aims at condensing some results on the 32-point approximate DFT and discussing its arithmetic complexity.
Discrete Fourier Transform Approximations Based on the Cooley-Tukey Radix-2 Algorithm
Feb 25, 2024



Abstract:This report elaborates on approximations for the discrete Fourier transform by means of replacing the exact Cooley-Tukey algorithm twiddle-factors by low-complexity integers, such as $0, \pm \frac{1}{2}, \pm 1$.
An Iterative Wavelet Threshold for Signal Denoising
Jul 20, 2023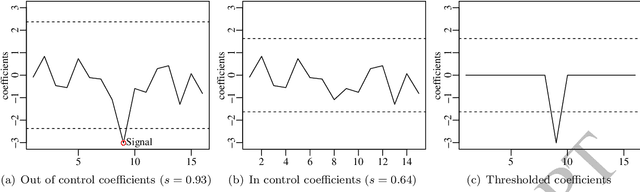
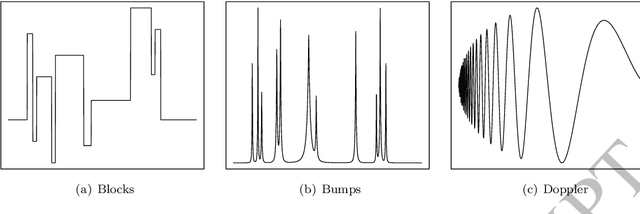
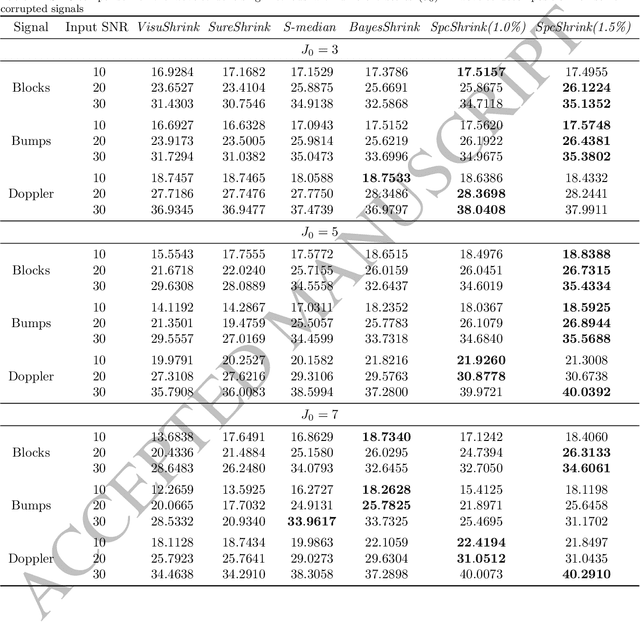
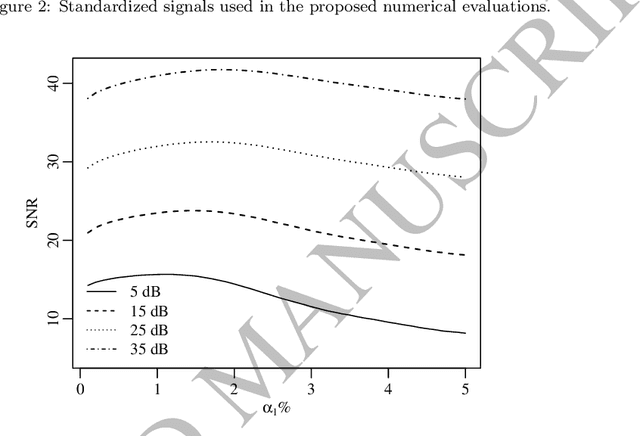
Abstract:This paper introduces an adaptive filtering process based on shrinking wavelet coefficients from the corresponding signal wavelet representation. The filtering procedure considers a threshold method determined by an iterative algorithm inspired by the control charts application, which is a tool of the statistical process control (SPC). The proposed method, called SpcShrink, is able to discriminate wavelet coefficients that significantly represent the signal of interest. The SpcShrink is algorithmically presented and numerically evaluated according to Monte Carlo simulations. Two empirical applications to real biomedical data filtering are also included and discussed. The SpcShrink shows superior performance when compared with competing algorithms.
* 19 pages, 10 figures, 2 tables
Low-complexity Multidimensional DCT Approximations
Jun 20, 2023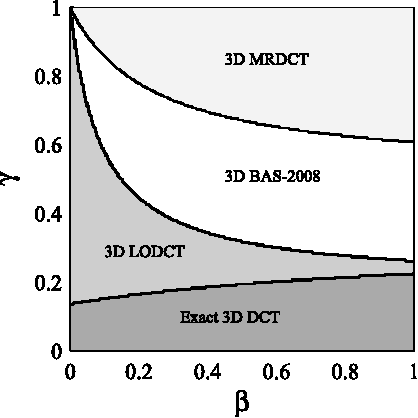
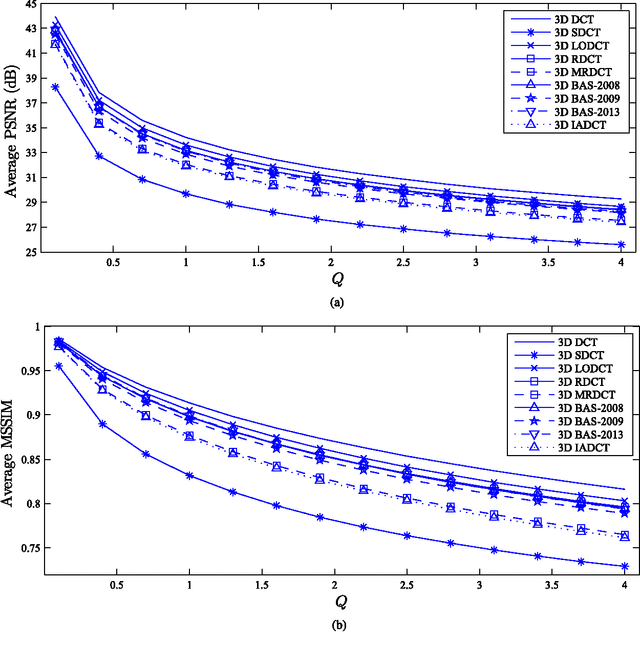

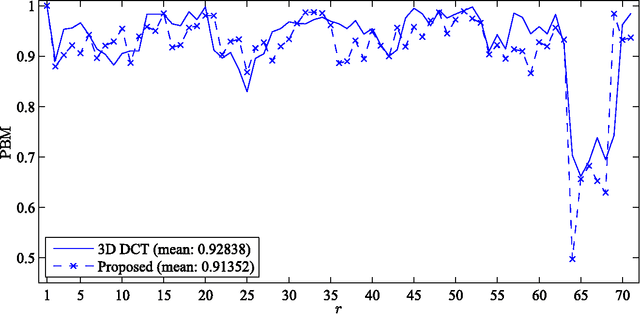
Abstract:In this paper, we introduce low-complexity multidimensional discrete cosine transform (DCT) approximations. Three dimensional DCT (3D DCT) approximations are formalized in terms of high-order tensor theory. The formulation is extended to higher dimensions with arbitrary lengths. Several multiplierless $8\times 8\times 8$ approximate methods are proposed and the computational complexity is discussed for the general multidimensional case. The proposed methods complexity cost was assessed, presenting considerably lower arithmetic operations when compared with the exact 3D DCT. The proposed approximations were embedded into 3D DCT-based video coding scheme and a modified quantization step was introduced. The simulation results showed that the approximate 3D DCT coding methods offer almost identical output visual quality when compared with exact 3D DCT scheme. The proposed 3D approximations were also employed as a tool for visual tracking. The approximate 3D DCT-based proposed system performs similarly to the original exact 3D DCT-based method. In general, the suggested methods showed competitive performance at a considerably lower computational cost.
* 28 pages, 5 figures, 5 tables
2-D Rayleigh Autoregressive Moving Average Model for SAR Image Modeling
Aug 07, 2022

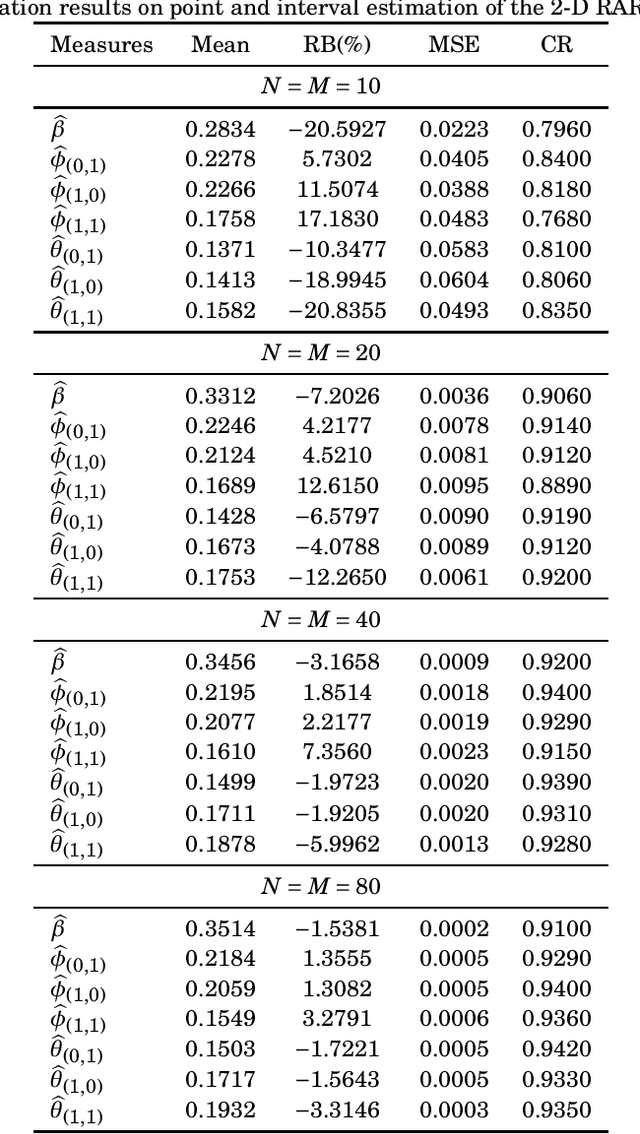
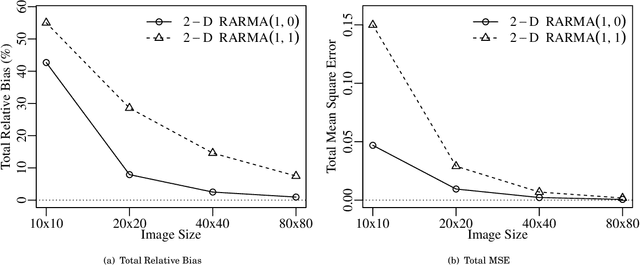
Abstract:Two-dimensional (2-D) autoregressive moving average (ARMA) models are commonly applied to describe real-world image data, usually assuming Gaussian or symmetric noise. However, real-world data often present non-Gaussian signals, with asymmetrical distributions and strictly positive values. In particular, SAR images are known to be well characterized by the Rayleigh distribution. In this context, the ARMA model tailored for 2-D Rayleigh-distributed data is introduced -- the 2-D RARMA model. The 2-D RARMA model is derived and conditional likelihood inferences are discussed. The proposed model was submitted to extensive Monte Carlo simulations to evaluate the performance of the conditional maximum likelihood estimators. Moreover, in the context of SAR image processing, two comprehensive numerical experiments were performed comparing anomaly detection and image modeling results of the proposed model with traditional 2-D ARMA models and competing methods in the literature.
* 21 pages, 8 figures, 6 tables
Improved Point Estimation for the Rayleigh Regression Model
Aug 07, 2022

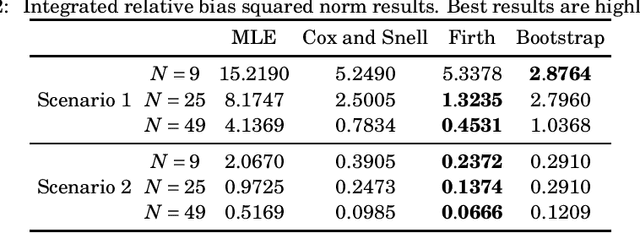

Abstract:The Rayleigh regression model was recently proposed for modeling amplitude values of synthetic aperture radar (SAR) image pixels. However, inferences from such model are based on the maximum likelihood estimators, which can be biased for small signal lengths. The Rayleigh regression model for SAR images often takes into account small pixel windows, which may lead to inaccurate results. In this letter, we introduce bias-adjusted estimators tailored for the Rayleigh regression model based on: (i) the Cox and Snell's method; (ii) the Firth's scheme; and (iii) the parametric bootstrap method. We present numerical experiments considering synthetic and actual SAR data sets. The bias-adjusted estimators yield nearly unbiased estimates and accurate modeling results.
* 7 pages, 1 figure, 4 tables
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge