Extensions on low-complexity DCT approximations for larger blocklengths based on minimal angle similarity

The discrete cosine transform (DCT) is a central tool for image and video coding because it can be related to the Karhunen-Lo\`eve transform (KLT), which is the optimal transform in terms of retained transform coefficients and data decorrelation. In this paper, we introduce 16-, 32-, and 64-point low-complexity DCT approximations by minimizing individually the angle between the rows of the exact DCT matrix and the matrix induced by the approximate transforms. According to some classical figures of merit, the proposed transforms outperformed the approximations for the DCT already known in the literature. Fast algorithms were also developed for the low-complexity transforms, asserting a good balance between the performance and its computational cost. Practical applications in image encoding showed the relevance of the transforms in this context. In fact, the experiments showed that the proposed transforms had better results than the known approximations in the literature for the cases of 16, 32, and 64 blocklength.

Low-Complexity Loeffler DCT Approximations for Image and Video Coding

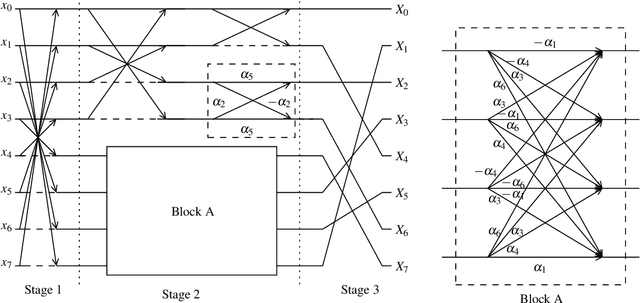
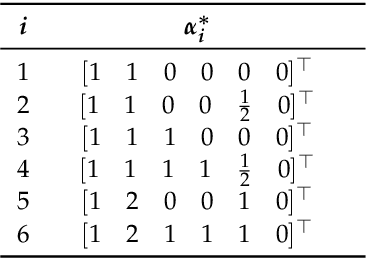
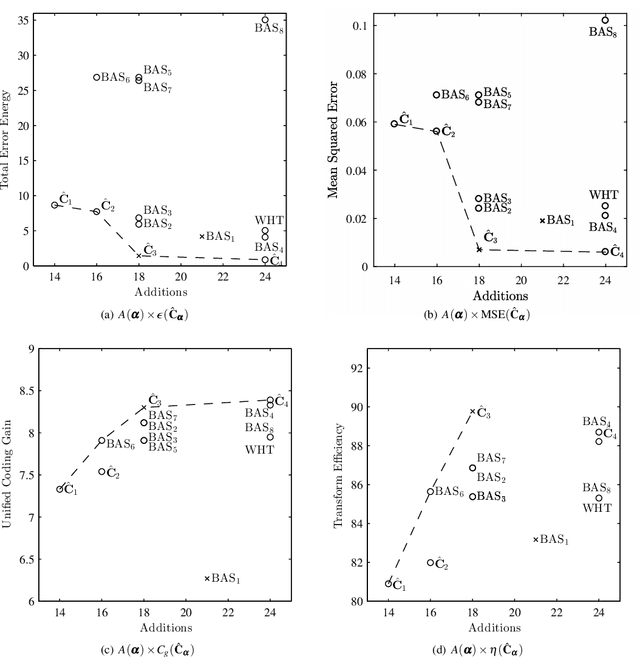
This paper introduced a matrix parametrization method based on the Loeffler discrete cosine transform (DCT) algorithm. As a result, a new class of eight-point DCT approximations was proposed, capable of unifying the mathematical formalism of several eight-point DCT approximations archived in the literature. Pareto-efficient DCT approximations are obtained through multicriteria optimization, where computational complexity, proximity, and coding performance are considered. Efficient approximations and their scaled 16- and 32-point versions are embedded into image and video encoders, including a JPEG-like codec and H.264/AVC and H.265/HEVC standards. Results are compared to the unmodified standard codecs. Efficient approximations are mapped and implemented on a Xilinx VLX240T FPGA and evaluated for area, speed, and power consumption.

Multiplierless 16-point DCT Approximation for Low-complexity Image and Video Coding

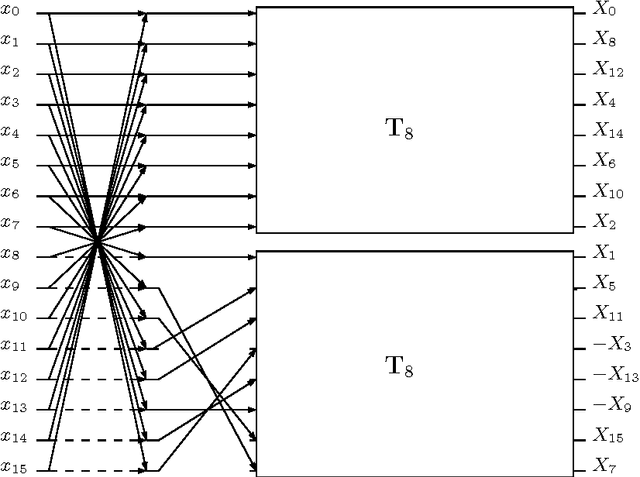
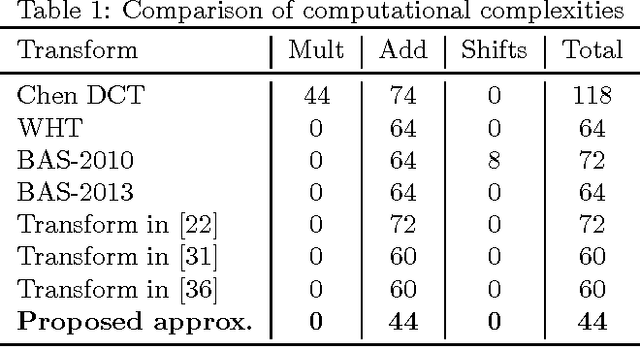
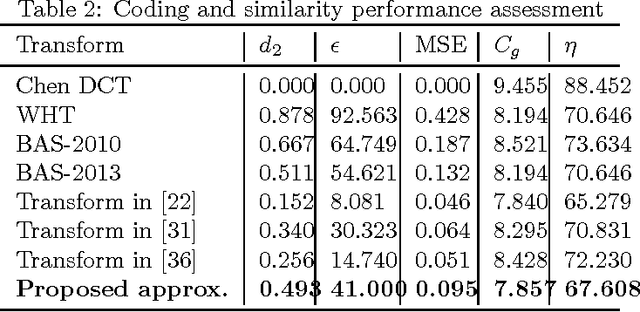
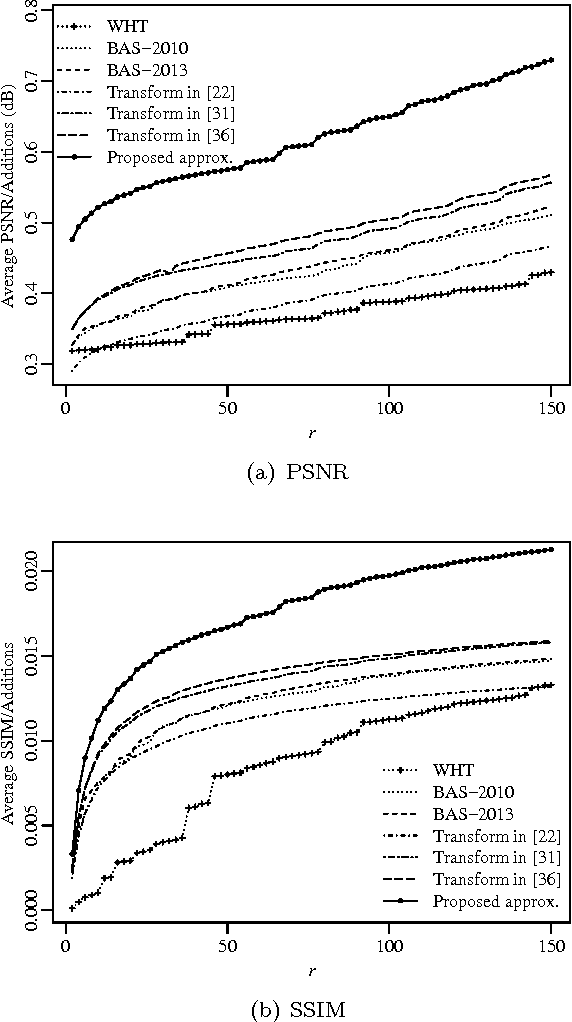
An orthogonal 16-point approximate discrete cosine transform (DCT) is introduced. The proposed transform requires neither multiplications nor bit-shifting operations. A fast algorithm based on matrix factorization is introduced, requiring only 44 additions---the lowest arithmetic cost in literature. To assess the introduced transform, computational complexity, similarity with the exact DCT, and coding performance measures are computed. Classical and state-of-the-art 16-point low-complexity transforms were used in a comparative analysis. In the context of image compression, the proposed approximation was evaluated via PSNR and SSIM measurements, attaining the best cost-benefit ratio among the competitors. For video encoding, the proposed approximation was embedded into a HEVC reference software for direct comparison with the original HEVC standard. Physically realized and tested using FPGA hardware, the proposed transform showed 35% and 37% improvements of area-time and area-time-squared VLSI metrics when compared to the best competing transform in the literature.