T. L. T. Silveira
Low-Complexity Loeffler DCT Approximations for Image and Video Coding
Jul 29, 2022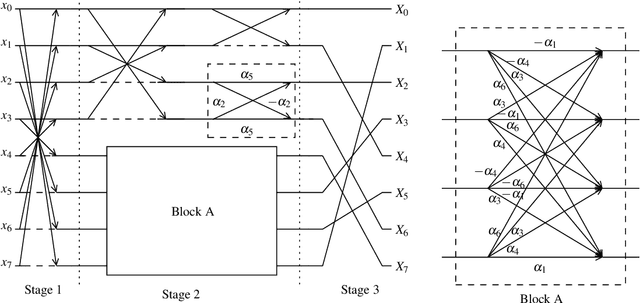
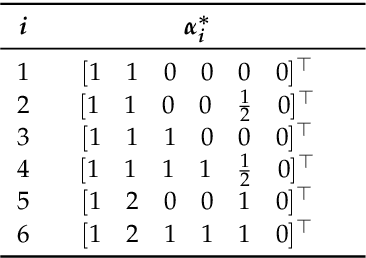

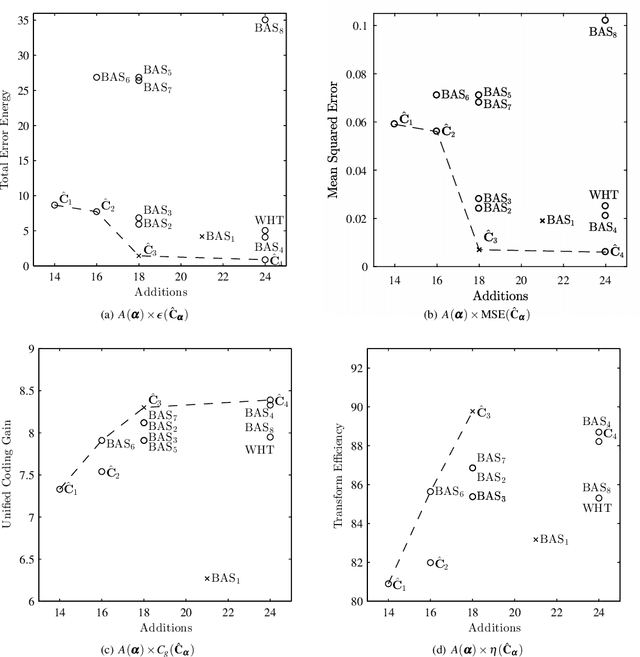
Abstract:This paper introduced a matrix parametrization method based on the Loeffler discrete cosine transform (DCT) algorithm. As a result, a new class of eight-point DCT approximations was proposed, capable of unifying the mathematical formalism of several eight-point DCT approximations archived in the literature. Pareto-efficient DCT approximations are obtained through multicriteria optimization, where computational complexity, proximity, and coding performance are considered. Efficient approximations and their scaled 16- and 32-point versions are embedded into image and video encoders, including a JPEG-like codec and H.264/AVC and H.265/HEVC standards. Results are compared to the unmodified standard codecs. Efficient approximations are mapped and implemented on a Xilinx VLX240T FPGA and evaluated for area, speed, and power consumption.
* 25 pages, 11 figures, 7 tables
Multiplierless 16-point DCT Approximation for Low-complexity Image and Video Coding
Jun 23, 2016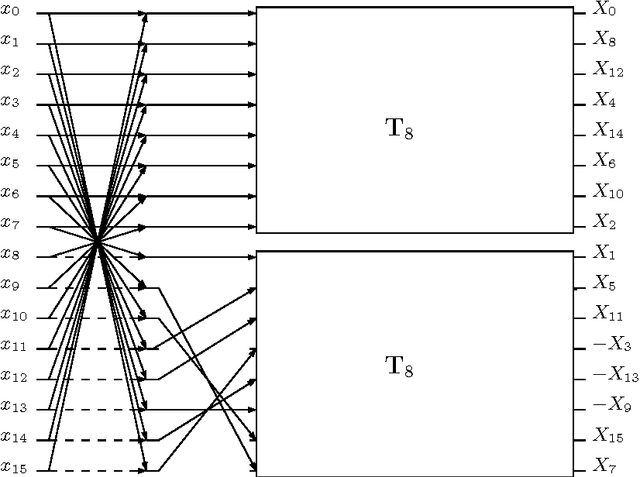
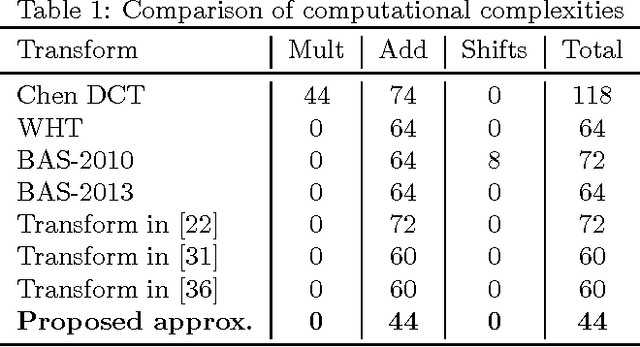
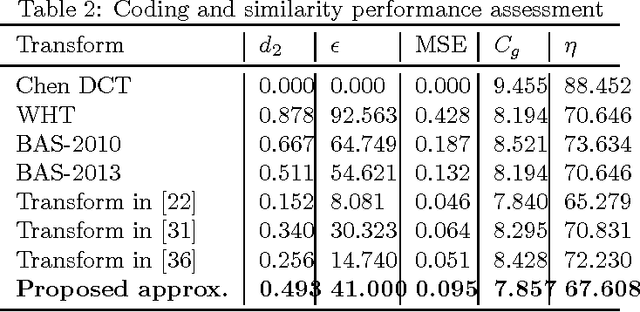
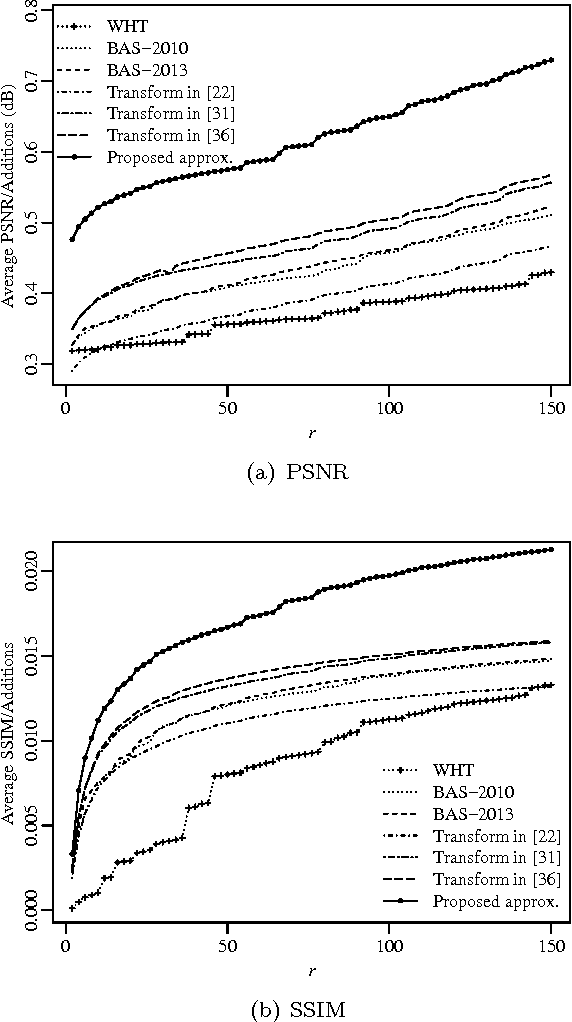
Abstract:An orthogonal 16-point approximate discrete cosine transform (DCT) is introduced. The proposed transform requires neither multiplications nor bit-shifting operations. A fast algorithm based on matrix factorization is introduced, requiring only 44 additions---the lowest arithmetic cost in literature. To assess the introduced transform, computational complexity, similarity with the exact DCT, and coding performance measures are computed. Classical and state-of-the-art 16-point low-complexity transforms were used in a comparative analysis. In the context of image compression, the proposed approximation was evaluated via PSNR and SSIM measurements, attaining the best cost-benefit ratio among the competitors. For video encoding, the proposed approximation was embedded into a HEVC reference software for direct comparison with the original HEVC standard. Physically realized and tested using FPGA hardware, the proposed transform showed 35% and 37% improvements of area-time and area-time-squared VLSI metrics when compared to the best competing transform in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge