Fast Data-independent KLT Approximations Based on Integer Functions

The Karhunen-Lo\`eve transform (KLT) stands as a well-established discrete transform, demonstrating optimal characteristics in data decorrelation and dimensionality reduction. Its ability to condense energy compression into a select few main components has rendered it instrumental in various applications within image compression frameworks. However, computing the KLT depends on the covariance matrix of the input data, which makes it difficult to develop fast algorithms for its implementation. Approximations for the KLT, utilizing specific rounding functions, have been introduced to reduce its computational complexity. Therefore, our paper introduces a category of low-complexity, data-independent KLT approximations, employing a range of round-off functions. The design methodology of the approximate transform is defined for any block-length $N$, but emphasis is given to transforms of $N = 8$ due to its wide use in image and video compression. The proposed transforms perform well when compared to the exact KLT and approximations considering classical performance measures. For particular scenarios, our proposed transforms demonstrated superior performance when compared to KLT approximations documented in the literature. We also developed fast algorithms for the proposed transforms, further reducing the arithmetic cost associated with their implementation. Evaluation of field programmable gate array (FPGA) hardware implementation metrics was conducted. Practical applications in image encoding showed the relevance of the proposed transforms. In fact, we showed that one of the proposed transforms outperformed the exact KLT given certain compression ratios.

Discrete Fourier Transform Approximations Based on the Cooley-Tukey Radix-2 Algorithm

This report elaborates on approximations for the discrete Fourier transform by means of replacing the exact Cooley-Tukey algorithm twiddle-factors by low-complexity integers, such as $0, \pm \frac{1}{2}, \pm 1$.

Low-Complexity Loeffler DCT Approximations for Image and Video Coding

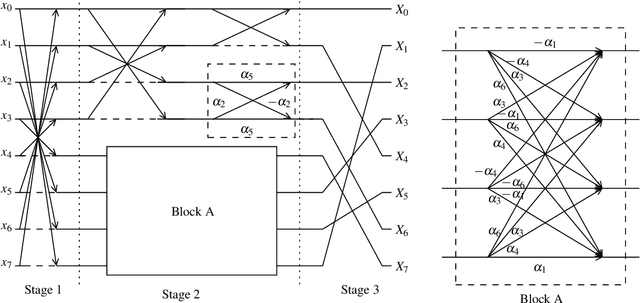
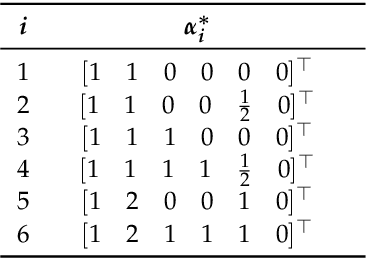
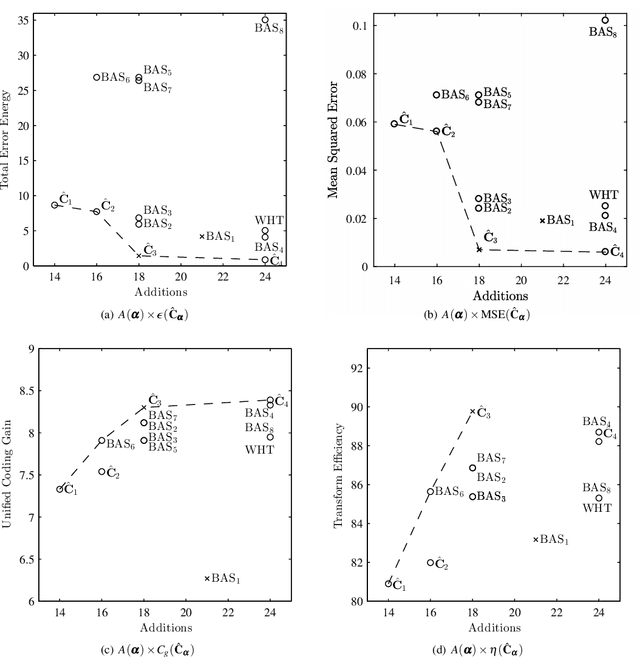
This paper introduced a matrix parametrization method based on the Loeffler discrete cosine transform (DCT) algorithm. As a result, a new class of eight-point DCT approximations was proposed, capable of unifying the mathematical formalism of several eight-point DCT approximations archived in the literature. Pareto-efficient DCT approximations are obtained through multicriteria optimization, where computational complexity, proximity, and coding performance are considered. Efficient approximations and their scaled 16- and 32-point versions are embedded into image and video encoders, including a JPEG-like codec and H.264/AVC and H.265/HEVC standards. Results are compared to the unmodified standard codecs. Efficient approximations are mapped and implemented on a Xilinx VLX240T FPGA and evaluated for area, speed, and power consumption.

A Class of Low-complexity DCT-like Transforms for Image and Video Coding

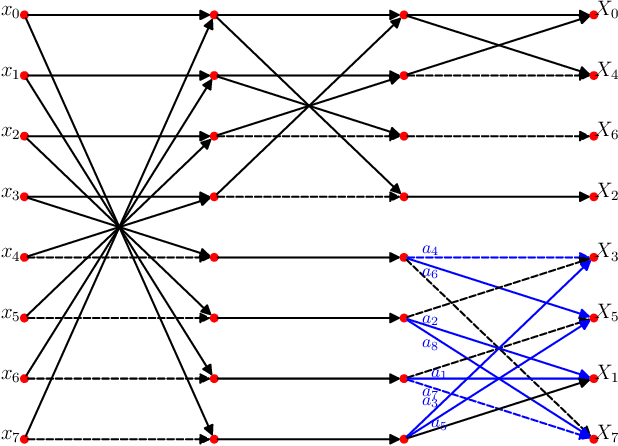
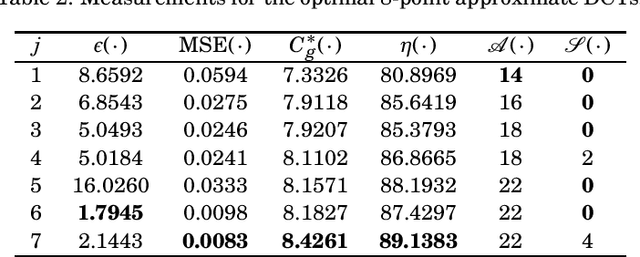
The discrete cosine transform (DCT) is a relevant tool in signal processing applications, mainly known for its good decorrelation properties. Current image and video coding standards -- such as JPEG and HEVC -- adopt the DCT as a fundamental building block for compression. Recent works have introduced low-complexity approximations for the DCT, which become paramount in applications demanding real-time computation and low-power consumption. The design of DCT approximations involves a trade-off between computational complexity and performance. This paper introduces a new multiparametric transform class encompassing the round-off DCT (RDCT) and the modified RDCT (MRDCT), two relevant multiplierless 8-point approximate DCTs. The associated fast algorithm is provided. Four novel orthogonal low-complexity 8-point DCT approximations are obtained by solving a multicriteria optimization problem. The optimal 8-point transforms are scaled to lengths 16 and 32 while keeping the arithmetic complexity low. The proposed methods are assessed by proximity and coding measures with respect to the exact DCT. Image and video coding experiments hardware realization are performed. The novel transforms perform close to or outperform the current state-of-the-art DCT approximations.

Low-complexity Scaling Methods for DCT-II Approximations

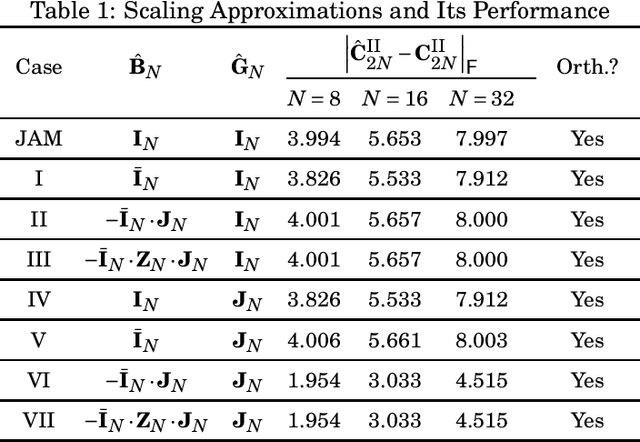
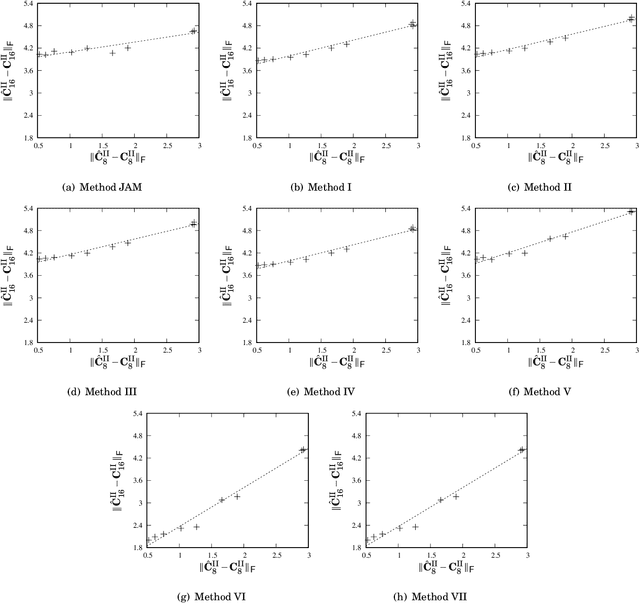
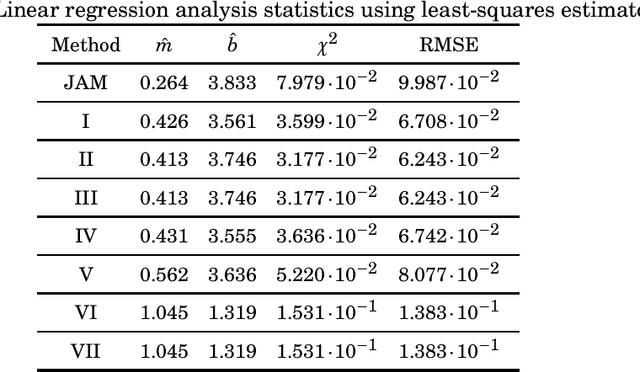
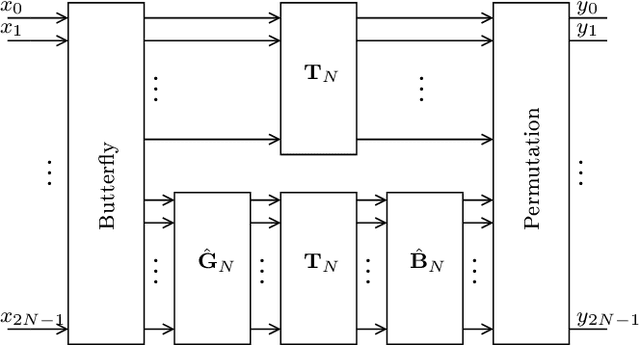
This paper introduces a collection of scaling methods for generating $2N$-point DCT-II approximations based on $N$-point low-complexity transformations. Such scaling is based on the Hou recursive matrix factorization of the exact $2N$-point DCT-II matrix. Encompassing the widely employed Jridi-Alfalou-Meher scaling method, the proposed techniques are shown to produce DCT-II approximations that outperform the transforms resulting from the JAM scaling method according to total error energy and mean squared error. Orthogonality conditions are derived and an extensive error analysis based on statistical simulation demonstrates the good performance of the introduced scaling methods. A hardware implementation is also provided demonstrating the competitiveness of the proposed methods when compared to the JAM scaling method.