Low-complexity Multidimensional DCT Approximations

In this paper, we introduce low-complexity multidimensional discrete cosine transform (DCT) approximations. Three dimensional DCT (3D DCT) approximations are formalized in terms of high-order tensor theory. The formulation is extended to higher dimensions with arbitrary lengths. Several multiplierless $8\times 8\times 8$ approximate methods are proposed and the computational complexity is discussed for the general multidimensional case. The proposed methods complexity cost was assessed, presenting considerably lower arithmetic operations when compared with the exact 3D DCT. The proposed approximations were embedded into 3D DCT-based video coding scheme and a modified quantization step was introduced. The simulation results showed that the approximate 3D DCT coding methods offer almost identical output visual quality when compared with exact 3D DCT scheme. The proposed 3D approximations were also employed as a tool for visual tracking. The approximate 3D DCT-based proposed system performs similarly to the original exact 3D DCT-based method. In general, the suggested methods showed competitive performance at a considerably lower computational cost.

Fast Radix-32 Approximate DFTs for 1024-Beam Digital RF Beamforming

The discrete Fourier transform (DFT) is widely employed for multi-beam digital beamforming. The DFT can be efficiently implemented through the use of fast Fourier transform (FFT) algorithms, thus reducing chip area, power consumption, processing time, and consumption of other hardware resources. This paper proposes three new hybrid DFT 1024-point DFT approximations and their respective fast algorithms. These approximate DFT (ADFT) algorithms have significantly reduced circuit complexity and power consumption compared to traditional FFT approaches while trading off a subtle loss in computational precision which is acceptable for digital beamforming applications in RF antenna implementations. ADFT algorithms have not been introduced for beamforming beyond $N = 32$, but this paper anticipates the need for massively large adaptive arrays for future 5G and 6G systems. Digital CMOS circuit designs for the ADFTs show the resulting improvements in both circuit complexity and power consumption metrics. Simulation results show similar or lower critical path delay with up to 48.5% lower chip area compared to a standard Cooley-Tukey FFT. The time-area and dynamic power metrics are reduced up to 66.0%. The 1024-point ADFT beamformers produce signal-to-noise ratio (SNR) gains between 29.2--30.1 dB, which is a loss of $\le$ 0.9 dB SNR gain compared to exact 1024-point DFT beamformers (worst case) realizable at using an FFT.

Low-complexity Three-dimensional Discrete Hartley Transform Approximations for Medical Image Compression

The discrete Hartley transform (DHT) is a useful tool for medical image coding. The three-dimensional DHT (3D DHT) can be employed to compress medical image data, such as magnetic resonance and X-ray angiography. However, the computation of the 3D DHT involves several multiplications by irrational quantities, which require floating-point arithmetic and inherent truncation errors. In recent years, a significant progress in wireless and implantable biomedical devices has been achieved. Such devices present critical power and hardware limitations. The multiplication operation demands higher hardware, power, and time consumption than other arithmetic operations, such as addition and bit-shifts. In this work, we present a set of multiplierless DHT approximations, which can be implemented with fixed-point arithmetic. We derive 3D DHT approximations by employing tensor formalism. Such proposed methods present prominent computational savings compared to the usual 3D DHT approach, being appropriate for devices with limited resources. The proposed transforms are applied in a lossy 3D DHT-based medical image compression algorithm, presenting practically the same level of visual quality ($>98\%$ in terms of SSIM) at a considerable reduction in computational effort ($100 \%$ multiplicative complexity reduction). Furthermore, we implemented the proposed 3D transforms in an ARM Cortex-M0+ processor employing the low-cost Raspberry Pi Pico board. The execution time was reduced by $\sim$70% compared to the usual 3D DHT and $\sim$90% compared to 3D DCT.

A Class of Low-complexity DCT-like Transforms for Image and Video Coding

The discrete cosine transform (DCT) is a relevant tool in signal processing applications, mainly known for its good decorrelation properties. Current image and video coding standards -- such as JPEG and HEVC -- adopt the DCT as a fundamental building block for compression. Recent works have introduced low-complexity approximations for the DCT, which become paramount in applications demanding real-time computation and low-power consumption. The design of DCT approximations involves a trade-off between computational complexity and performance. This paper introduces a new multiparametric transform class encompassing the round-off DCT (RDCT) and the modified RDCT (MRDCT), two relevant multiplierless 8-point approximate DCTs. The associated fast algorithm is provided. Four novel orthogonal low-complexity 8-point DCT approximations are obtained by solving a multicriteria optimization problem. The optimal 8-point transforms are scaled to lengths 16 and 32 while keeping the arithmetic complexity low. The proposed methods are assessed by proximity and coding measures with respect to the exact DCT. Image and video coding experiments hardware realization are performed. The novel transforms perform close to or outperform the current state-of-the-art DCT approximations.

A Multiplierless Pruned DCT-like Transformation for Image and Video Compression that Requires 10 Additions Only

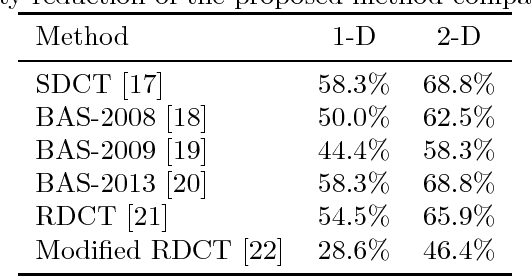
A multiplierless pruned approximate 8-point discrete cosine transform (DCT) requiring only 10 additions is introduced. The proposed algorithm was assessed in image and video compression, showing competitive performance with state-of-the-art methods. Digital implementation in 45 nm CMOS technology up to place-and-route level indicates clock speed of 288 MHz at a 1.1 V supply. The 8x8 block rate is 36 MHz.The DCT approximation was embedded into HEVC reference software; resulting video frames, at up to 327 Hz for 8-bit RGB HEVC, presented negligible image degradation.