Fast Data-independent KLT Approximations Based on Integer Functions

The Karhunen-Lo\`eve transform (KLT) stands as a well-established discrete transform, demonstrating optimal characteristics in data decorrelation and dimensionality reduction. Its ability to condense energy compression into a select few main components has rendered it instrumental in various applications within image compression frameworks. However, computing the KLT depends on the covariance matrix of the input data, which makes it difficult to develop fast algorithms for its implementation. Approximations for the KLT, utilizing specific rounding functions, have been introduced to reduce its computational complexity. Therefore, our paper introduces a category of low-complexity, data-independent KLT approximations, employing a range of round-off functions. The design methodology of the approximate transform is defined for any block-length $N$, but emphasis is given to transforms of $N = 8$ due to its wide use in image and video compression. The proposed transforms perform well when compared to the exact KLT and approximations considering classical performance measures. For particular scenarios, our proposed transforms demonstrated superior performance when compared to KLT approximations documented in the literature. We also developed fast algorithms for the proposed transforms, further reducing the arithmetic cost associated with their implementation. Evaluation of field programmable gate array (FPGA) hardware implementation metrics was conducted. Practical applications in image encoding showed the relevance of the proposed transforms. In fact, we showed that one of the proposed transforms outperformed the exact KLT given certain compression ratios.

Low-Complexity Loeffler DCT Approximations for Image and Video Coding

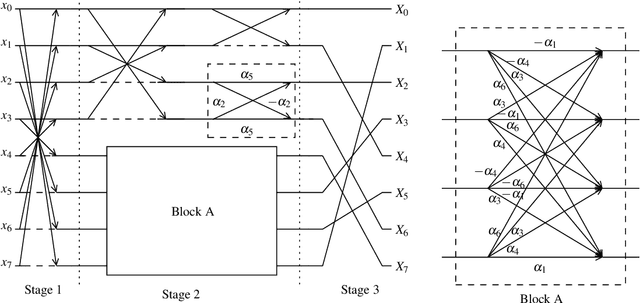
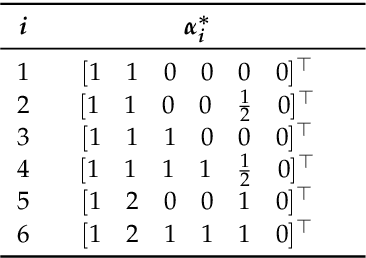
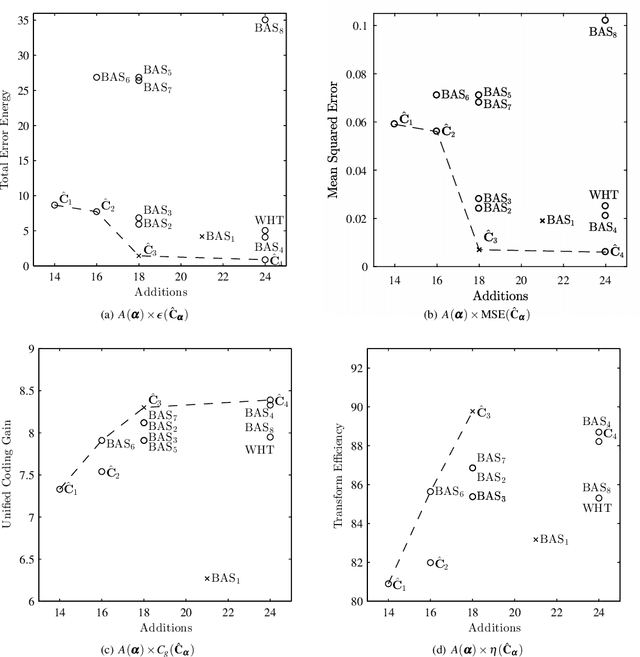
This paper introduced a matrix parametrization method based on the Loeffler discrete cosine transform (DCT) algorithm. As a result, a new class of eight-point DCT approximations was proposed, capable of unifying the mathematical formalism of several eight-point DCT approximations archived in the literature. Pareto-efficient DCT approximations are obtained through multicriteria optimization, where computational complexity, proximity, and coding performance are considered. Efficient approximations and their scaled 16- and 32-point versions are embedded into image and video encoders, including a JPEG-like codec and H.264/AVC and H.265/HEVC standards. Results are compared to the unmodified standard codecs. Efficient approximations are mapped and implemented on a Xilinx VLX240T FPGA and evaluated for area, speed, and power consumption.

Fast Radix-32 Approximate DFTs for 1024-Beam Digital RF Beamforming

The discrete Fourier transform (DFT) is widely employed for multi-beam digital beamforming. The DFT can be efficiently implemented through the use of fast Fourier transform (FFT) algorithms, thus reducing chip area, power consumption, processing time, and consumption of other hardware resources. This paper proposes three new hybrid DFT 1024-point DFT approximations and their respective fast algorithms. These approximate DFT (ADFT) algorithms have significantly reduced circuit complexity and power consumption compared to traditional FFT approaches while trading off a subtle loss in computational precision which is acceptable for digital beamforming applications in RF antenna implementations. ADFT algorithms have not been introduced for beamforming beyond $N = 32$, but this paper anticipates the need for massively large adaptive arrays for future 5G and 6G systems. Digital CMOS circuit designs for the ADFTs show the resulting improvements in both circuit complexity and power consumption metrics. Simulation results show similar or lower critical path delay with up to 48.5% lower chip area compared to a standard Cooley-Tukey FFT. The time-area and dynamic power metrics are reduced up to 66.0%. The 1024-point ADFT beamformers produce signal-to-noise ratio (SNR) gains between 29.2--30.1 dB, which is a loss of $\le$ 0.9 dB SNR gain compared to exact 1024-point DFT beamformers (worst case) realizable at using an FFT.

Radix-2 Self-Recursive Sparse Factorizations of Delay Vandermonde Matrices for Wideband Multi-Beam Antenna Arrays

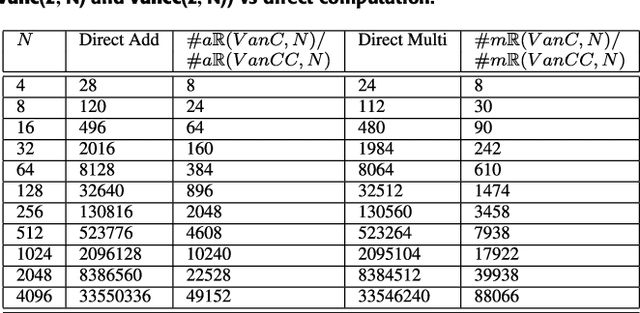
This paper presents a self-contained factorization for the Vandermonde matrices associated with true-time delay based wideband analog multi-beam beamforming using antenna arrays. The proposed factorization contains sparse and orthogonal matrices. Novel self-recursive radix-2 algorithms for Vandermonde matrices associated with true time delay based delay-sum filterbanks are presented to reduce the circuit complexity of multi-beam analog beamforming systems. The proposed algorithms for Vandermonde matrices by a vector attain $\mathcal{O}(N \log N)$ delay-amplifier circuit counts. Error bounds for the Vandermode matrices associated with true-time delay are established and then analyzed for numerical stability. The potential for real-world circuit implementation of the proposed algorithms will be shown through signal flow graphs that are the starting point for high-frequency analog circuit realizations.

Efficient and Self-Recursive Delay Vandermonde Algorithm for Multi-Beam Antenna Arrays

This paper presents a self-contained factorization for the delay Vandermonde matrix (DVM), which is the super class of the discrete Fourier transform, using sparse and companion matrices. An efficient DVM algorithm is proposed to reduce the complexity of radio-frequency (RF) $N$-beam analog beamforming systems. There exist applications for wideband multi-beam beamformers in wireless communication networks such as 5G/6G systems, system capacity can be improved by exploiting the improvement of the signal to noise ratio (SNR) using coherent summation of propagating waves based on their directions of propagation. The presence of a multitude of RF beams allows multiple independent wireless links to be established at high SNR, or used in conjunction with multiple-input multiple-output (MIMO) wireless systems, with the overall goal of improving system SNR and therefore capacity. To realize such multi-beam beamformers at acceptable analog circuit complexities, we use sparse factorization of the DVM in order to derive a low arithmetic complexity DVM algorithm. The paper also establishes an error bound and stability analysis of the proposed DVM algorithm. The proposed efficient DVM algorithm is aimed at implementation using analog realizations. For purposes of evaluation, the algorithm can be realized using both digital hardware as well as software defined radio platforms.

Low-complexity Scaling Methods for DCT-II Approximations

This paper introduces a collection of scaling methods for generating $2N$-point DCT-II approximations based on $N$-point low-complexity transformations. Such scaling is based on the Hou recursive matrix factorization of the exact $2N$-point DCT-II matrix. Encompassing the widely employed Jridi-Alfalou-Meher scaling method, the proposed techniques are shown to produce DCT-II approximations that outperform the transforms resulting from the JAM scaling method according to total error energy and mean squared error. Orthogonality conditions are derived and an extensive error analysis based on statistical simulation demonstrates the good performance of the introduced scaling methods. A hardware implementation is also provided demonstrating the competitiveness of the proposed methods when compared to the JAM scaling method.

Low-complexity Image and Video Coding Based on an Approximate Discrete Tchebichef Transform

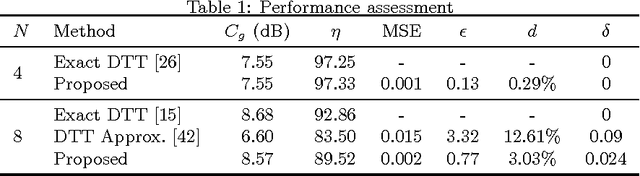
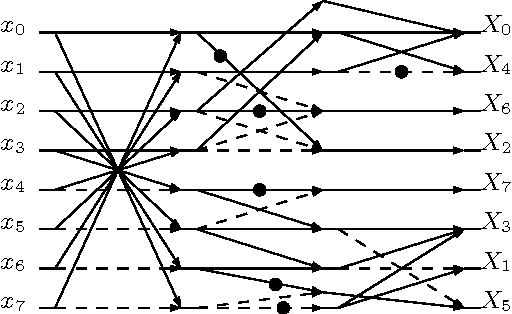
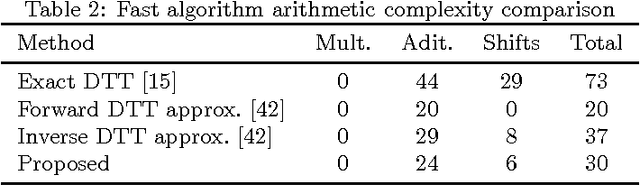
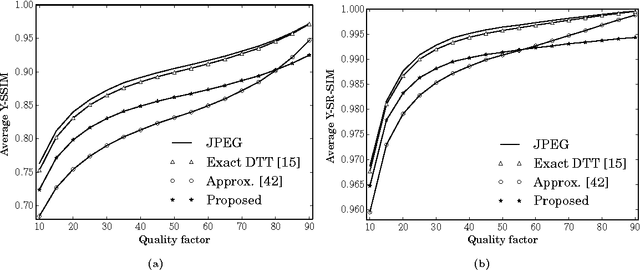
The usage of linear transformations has great relevance for data decorrelation applications, like image and video compression. In that sense, the discrete Tchebichef transform (DTT) possesses useful coding and decorrelation properties. The DTT transform kernel does not depend on the input data and fast algorithms can be developed to real time applications. However, the DTT fast algorithm presented in literature possess high computational complexity. In this work, we introduce a new low-complexity approximation for the DTT. The fast algorithm of the proposed transform is multiplication-free and requires a reduced number of additions and bit-shifting operations. Image and video compression simulations in popular standards shows good performance of the proposed transform. Regarding hardware resource consumption for FPGA shows 43.1% reduction of configurable logic blocks and ASIC place and route realization shows 57.7% reduction in the area-time figure when compared with the 2-D version of the exact DTT.

A Multiplierless Pruned DCT-like Transformation for Image and Video Compression that Requires 10 Additions Only

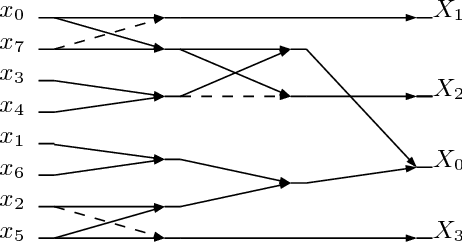
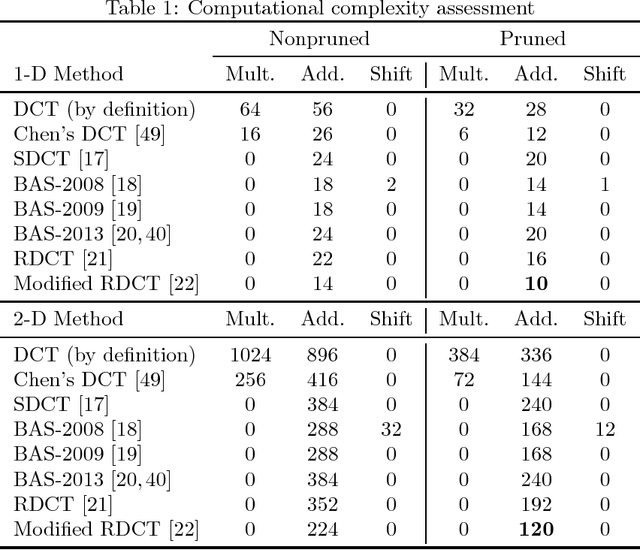
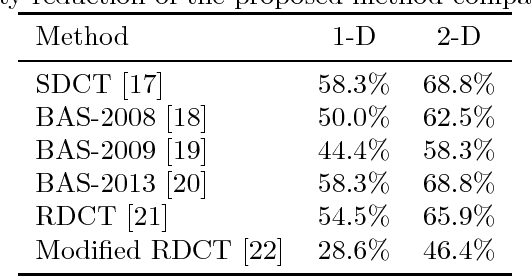
A multiplierless pruned approximate 8-point discrete cosine transform (DCT) requiring only 10 additions is introduced. The proposed algorithm was assessed in image and video compression, showing competitive performance with state-of-the-art methods. Digital implementation in 45 nm CMOS technology up to place-and-route level indicates clock speed of 288 MHz at a 1.1 V supply. The 8x8 block rate is 36 MHz.The DCT approximation was embedded into HEVC reference software; resulting video frames, at up to 327 Hz for 8-bit RGB HEVC, presented negligible image degradation.

Multiplierless 16-point DCT Approximation for Low-complexity Image and Video Coding

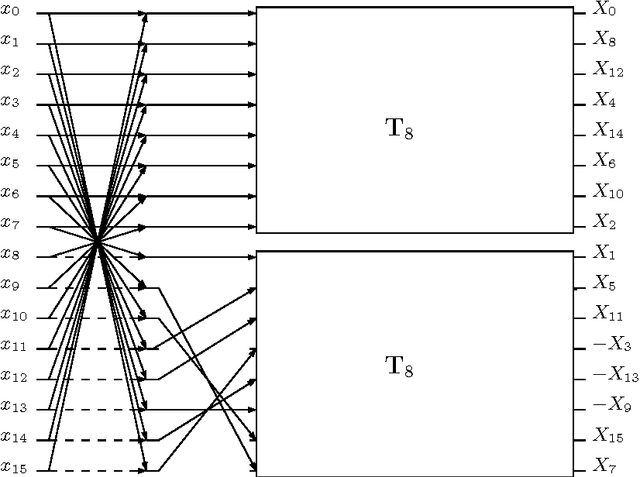
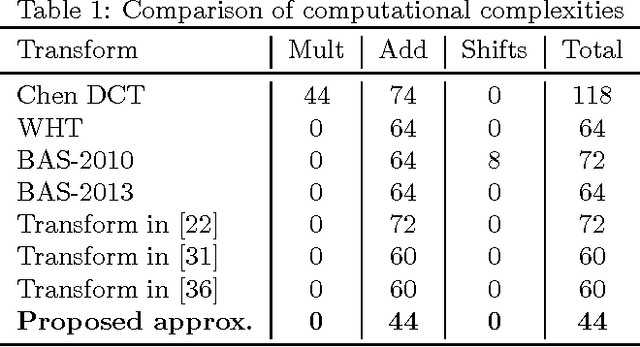
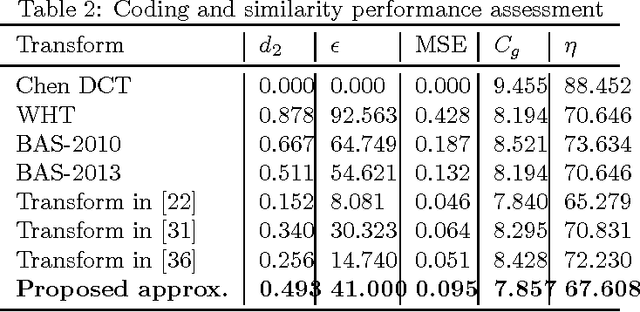
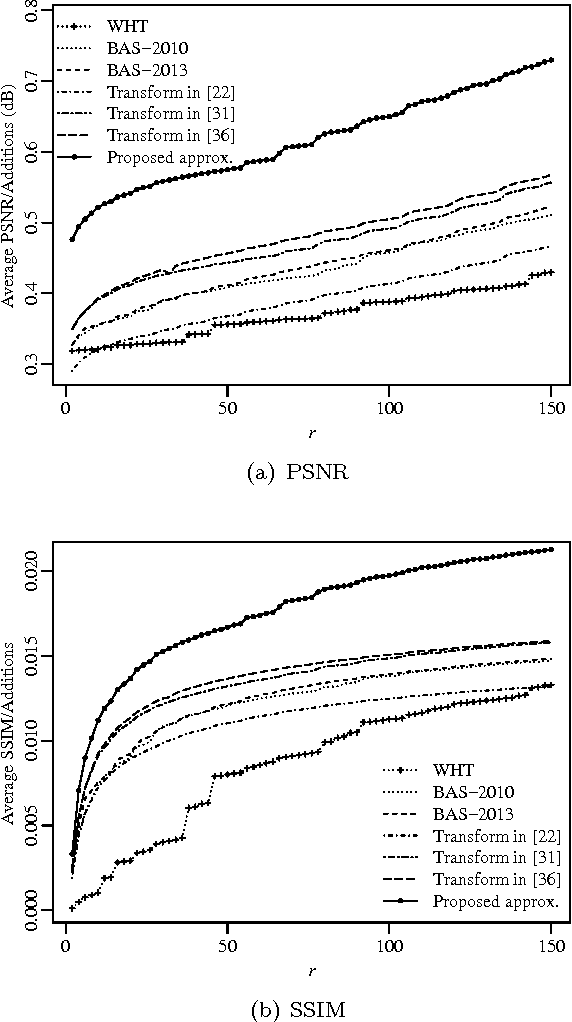
An orthogonal 16-point approximate discrete cosine transform (DCT) is introduced. The proposed transform requires neither multiplications nor bit-shifting operations. A fast algorithm based on matrix factorization is introduced, requiring only 44 additions---the lowest arithmetic cost in literature. To assess the introduced transform, computational complexity, similarity with the exact DCT, and coding performance measures are computed. Classical and state-of-the-art 16-point low-complexity transforms were used in a comparative analysis. In the context of image compression, the proposed approximation was evaluated via PSNR and SSIM measurements, attaining the best cost-benefit ratio among the competitors. For video encoding, the proposed approximation was embedded into a HEVC reference software for direct comparison with the original HEVC standard. Physically realized and tested using FPGA hardware, the proposed transform showed 35% and 37% improvements of area-time and area-time-squared VLSI metrics when compared to the best competing transform in the literature.

A Discrete Tchebichef Transform Approximation for Image and Video Coding

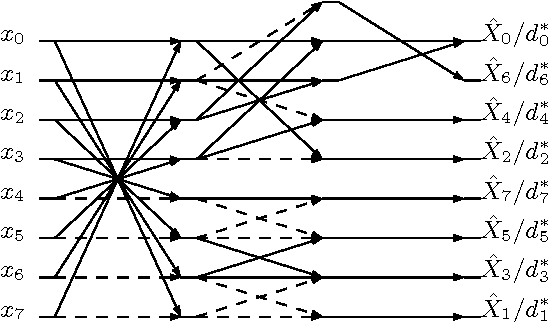
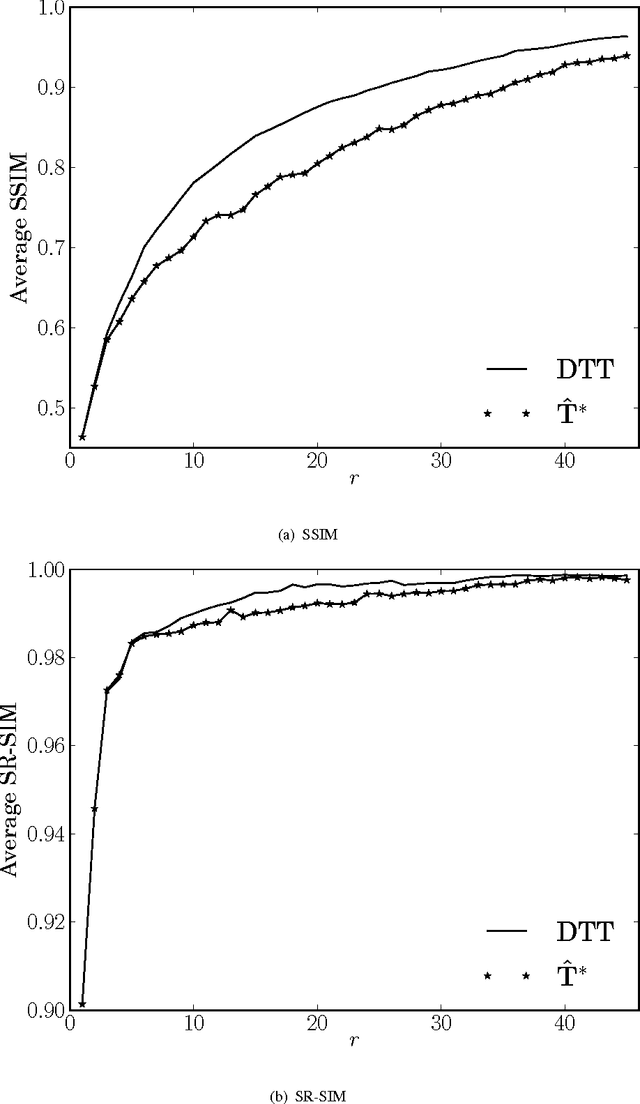
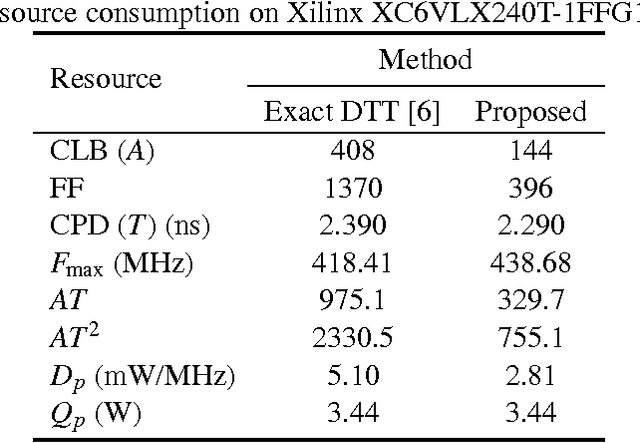
In this paper, we introduce a low-complexity approximation for the discrete Tchebichef transform (DTT). The proposed forward and inverse transforms are multiplication-free and require a reduced number of additions and bit-shifting operations. Numerical compression simulations demonstrate the efficiency of the proposed transform for image and video coding. Furthermore, Xilinx Virtex-6 FPGA based hardware realization shows 44.9% reduction in dynamic power consumption and 64.7% lower area when compared to the literature.