Low-complexity Image and Video Coding Based on an Approximate Discrete Tchebichef Transform

The usage of linear transformations has great relevance for data decorrelation applications, like image and video compression. In that sense, the discrete Tchebichef transform (DTT) possesses useful coding and decorrelation properties. The DTT transform kernel does not depend on the input data and fast algorithms can be developed to real time applications. However, the DTT fast algorithm presented in literature possess high computational complexity. In this work, we introduce a new low-complexity approximation for the DTT. The fast algorithm of the proposed transform is multiplication-free and requires a reduced number of additions and bit-shifting operations. Image and video compression simulations in popular standards shows good performance of the proposed transform. Regarding hardware resource consumption for FPGA shows 43.1% reduction of configurable logic blocks and ASIC place and route realization shows 57.7% reduction in the area-time figure when compared with the 2-D version of the exact DTT.

A Discrete Tchebichef Transform Approximation for Image and Video Coding

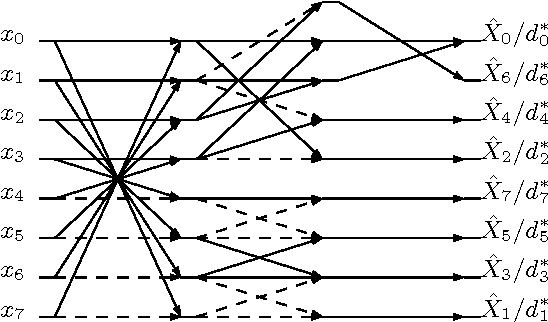
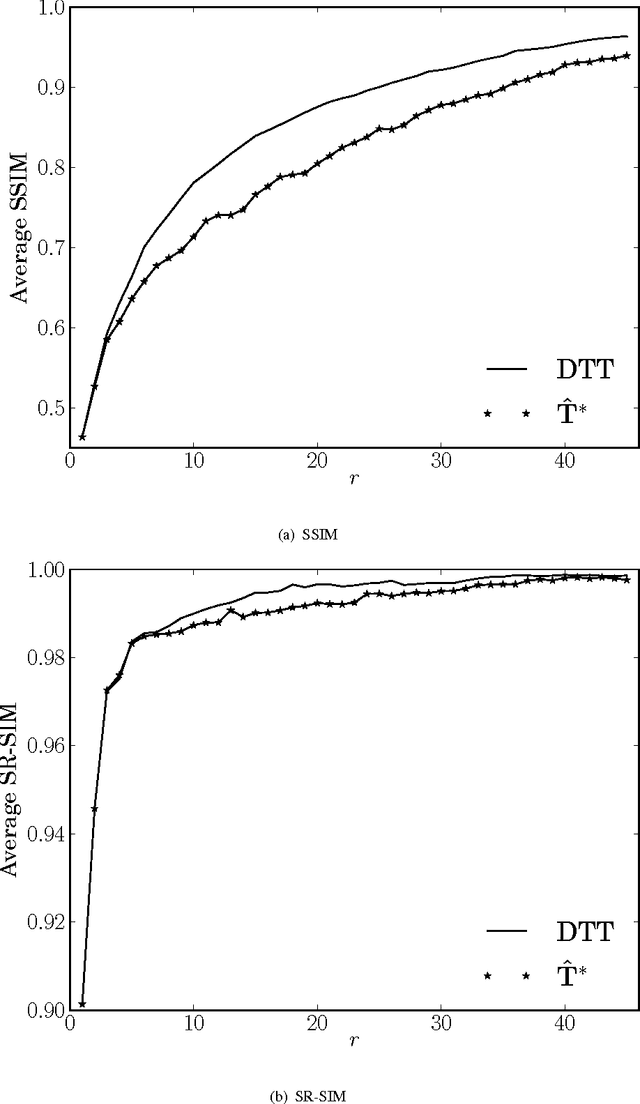
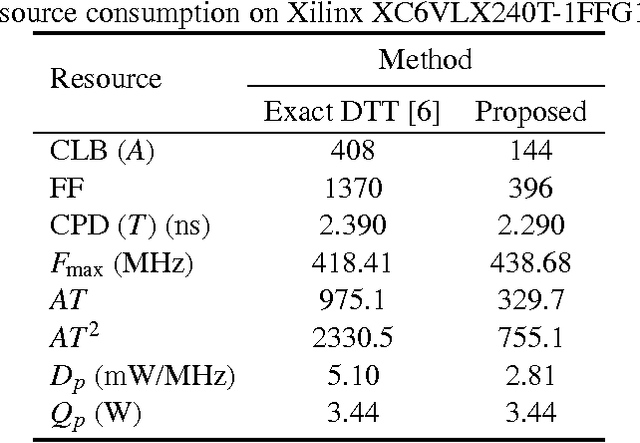
In this paper, we introduce a low-complexity approximation for the discrete Tchebichef transform (DTT). The proposed forward and inverse transforms are multiplication-free and require a reduced number of additions and bit-shifting operations. Numerical compression simulations demonstrate the efficiency of the proposed transform for image and video coding. Furthermore, Xilinx Virtex-6 FPGA based hardware realization shows 44.9% reduction in dynamic power consumption and 64.7% lower area when compared to the literature.