Extensions on low-complexity DCT approximations for larger blocklengths based on minimal angle similarity

The discrete cosine transform (DCT) is a central tool for image and video coding because it can be related to the Karhunen-Lo\`eve transform (KLT), which is the optimal transform in terms of retained transform coefficients and data decorrelation. In this paper, we introduce 16-, 32-, and 64-point low-complexity DCT approximations by minimizing individually the angle between the rows of the exact DCT matrix and the matrix induced by the approximate transforms. According to some classical figures of merit, the proposed transforms outperformed the approximations for the DCT already known in the literature. Fast algorithms were also developed for the low-complexity transforms, asserting a good balance between the performance and its computational cost. Practical applications in image encoding showed the relevance of the transforms in this context. In fact, the experiments showed that the proposed transforms had better results than the known approximations in the literature for the cases of 16, 32, and 64 blocklength.

Fast Data-independent KLT Approximations Based on Integer Functions

The Karhunen-Lo\`eve transform (KLT) stands as a well-established discrete transform, demonstrating optimal characteristics in data decorrelation and dimensionality reduction. Its ability to condense energy compression into a select few main components has rendered it instrumental in various applications within image compression frameworks. However, computing the KLT depends on the covariance matrix of the input data, which makes it difficult to develop fast algorithms for its implementation. Approximations for the KLT, utilizing specific rounding functions, have been introduced to reduce its computational complexity. Therefore, our paper introduces a category of low-complexity, data-independent KLT approximations, employing a range of round-off functions. The design methodology of the approximate transform is defined for any block-length $N$, but emphasis is given to transforms of $N = 8$ due to its wide use in image and video compression. The proposed transforms perform well when compared to the exact KLT and approximations considering classical performance measures. For particular scenarios, our proposed transforms demonstrated superior performance when compared to KLT approximations documented in the literature. We also developed fast algorithms for the proposed transforms, further reducing the arithmetic cost associated with their implementation. Evaluation of field programmable gate array (FPGA) hardware implementation metrics was conducted. Practical applications in image encoding showed the relevance of the proposed transforms. In fact, we showed that one of the proposed transforms outperformed the exact KLT given certain compression ratios.

Low-complexity Rounded KLT Approximation for Image Compression

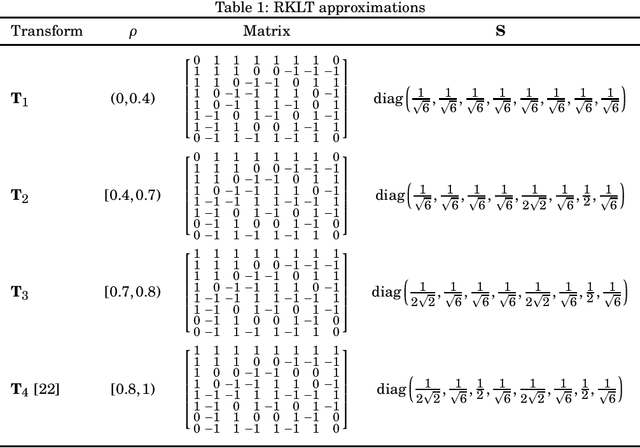
The Karhunen-Lo\`eve transform (KLT) is often used for data decorrelation and dimensionality reduction. Because its computation depends on the matrix of covariances of the input signal, the use of the KLT in real-time applications is severely constrained by the difficulty in developing fast algorithms to implement it. In this context, this paper proposes a new class of low-complexity transforms that are obtained through the application of the round function to the elements of the KLT matrix. The proposed transforms are evaluated considering figures of merit that measure the coding power and distance of the proposed approximations to the exact KLT and are also explored in image compression experiments. Fast algorithms are introduced for the proposed approximate transforms. It was shown that the proposed transforms perform well in image compression and require a low implementation cost.

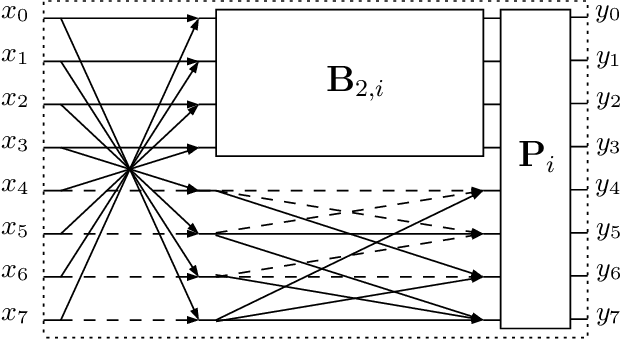
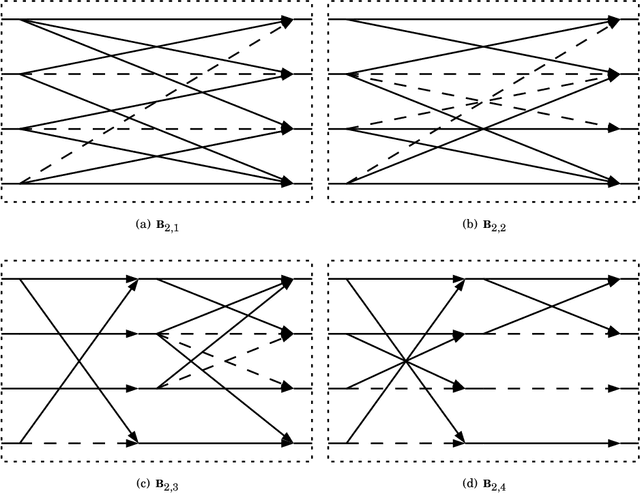
Data-independent Low-complexity KLT Approximations for Image and Video Coding

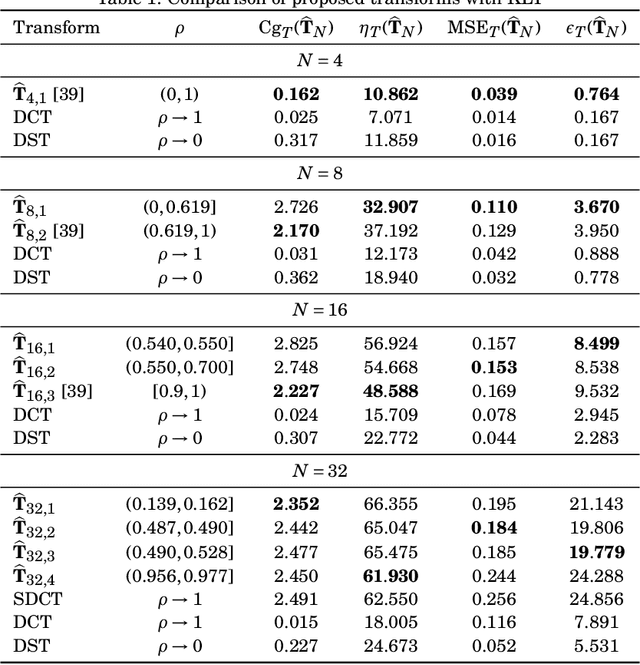
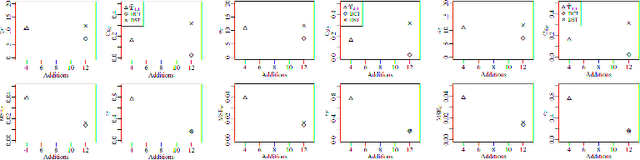
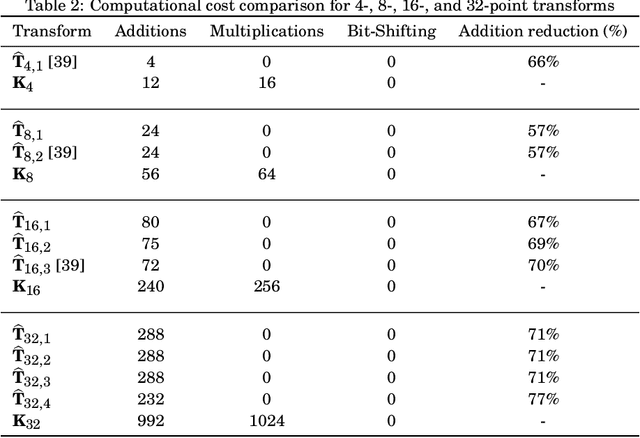
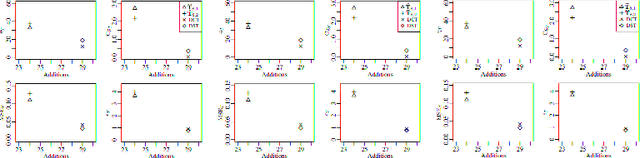
The Karhunen-Lo\`eve transform (KLT) is often used for data decorrelation and dimensionality reduction. The KLT is able to optimally retain the signal energy in only few transform components, being mathematically suitable for image and video compression. However, in practice, because of its high computational cost and dependence on the input signal, its application in real-time scenarios is precluded. This work proposes low-computational cost approximations for the KLT. We focus on the blocklengths $N \in \{4, 8, 16, 32 \}$ because they are widely employed in image and video coding standards such as JPEG and high efficiency video coding (HEVC). Extensive computational experiments demonstrate the suitability of the proposed low-complexity transforms for image and video compression.