Data-independent Low-complexity KLT Approximations for Image and Video Coding

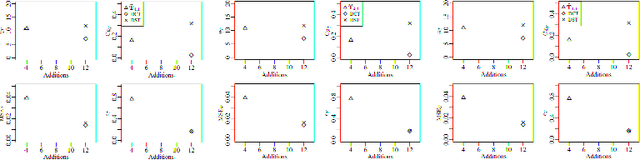
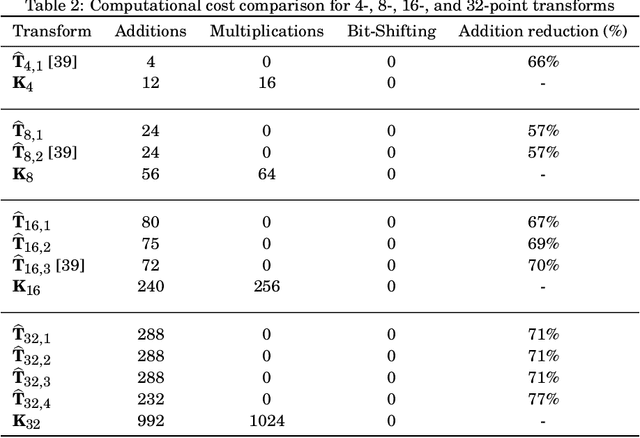
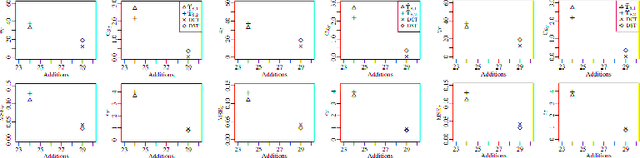
The Karhunen-Lo\`eve transform (KLT) is often used for data decorrelation and dimensionality reduction. The KLT is able to optimally retain the signal energy in only few transform components, being mathematically suitable for image and video compression. However, in practice, because of its high computational cost and dependence on the input signal, its application in real-time scenarios is precluded. This work proposes low-computational cost approximations for the KLT. We focus on the blocklengths $N \in \{4, 8, 16, 32 \}$ because they are widely employed in image and video coding standards such as JPEG and high efficiency video coding (HEVC). Extensive computational experiments demonstrate the suitability of the proposed low-complexity transforms for image and video compression.