Low-complexity Rounded KLT Approximation for Image Compression
Paper and Code
Nov 28, 2021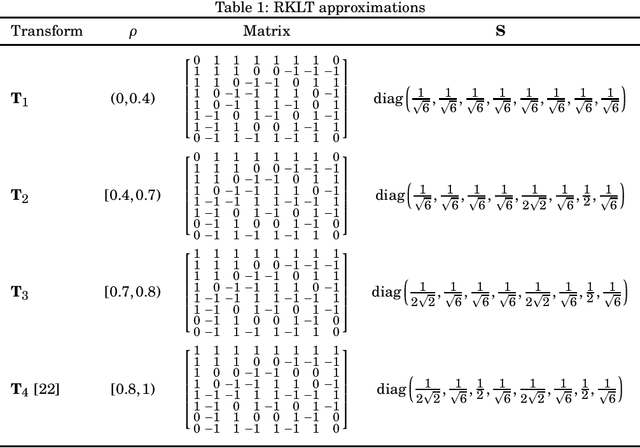
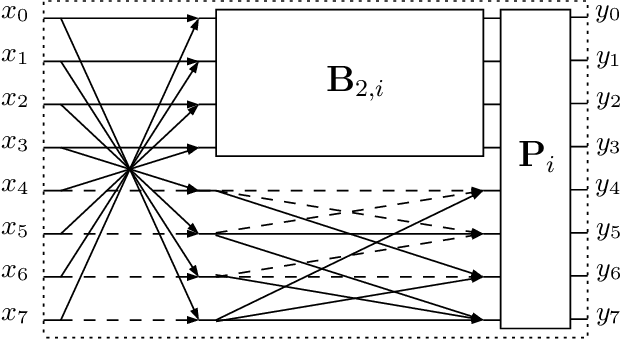

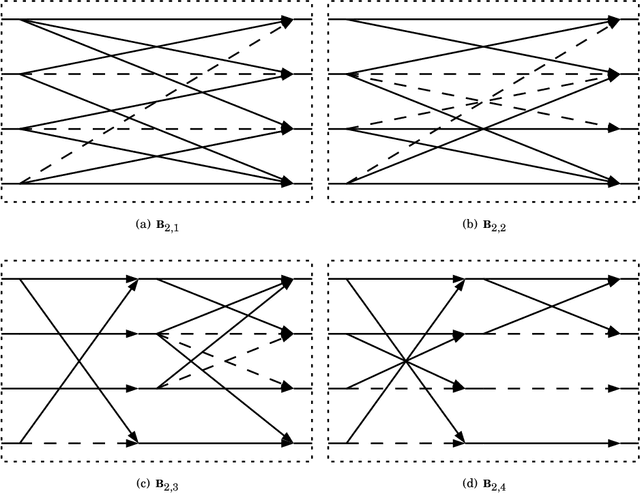
The Karhunen-Lo\`eve transform (KLT) is often used for data decorrelation and dimensionality reduction. Because its computation depends on the matrix of covariances of the input signal, the use of the KLT in real-time applications is severely constrained by the difficulty in developing fast algorithms to implement it. In this context, this paper proposes a new class of low-complexity transforms that are obtained through the application of the round function to the elements of the KLT matrix. The proposed transforms are evaluated considering figures of merit that measure the coding power and distance of the proposed approximations to the exact KLT and are also explored in image compression experiments. Fast algorithms are introduced for the proposed approximate transforms. It was shown that the proposed transforms perform well in image compression and require a low implementation cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge