A Class of Low-complexity DCT-like Transforms for Image and Video Coding

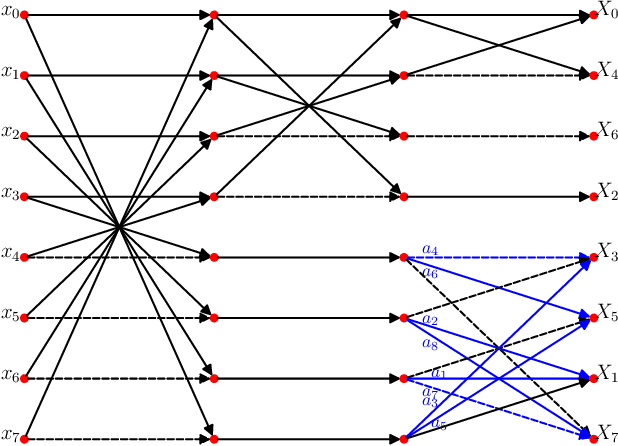
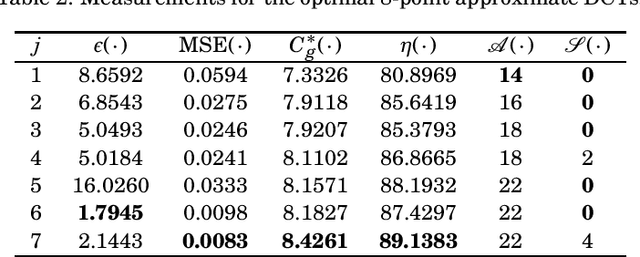
The discrete cosine transform (DCT) is a relevant tool in signal processing applications, mainly known for its good decorrelation properties. Current image and video coding standards -- such as JPEG and HEVC -- adopt the DCT as a fundamental building block for compression. Recent works have introduced low-complexity approximations for the DCT, which become paramount in applications demanding real-time computation and low-power consumption. The design of DCT approximations involves a trade-off between computational complexity and performance. This paper introduces a new multiparametric transform class encompassing the round-off DCT (RDCT) and the modified RDCT (MRDCT), two relevant multiplierless 8-point approximate DCTs. The associated fast algorithm is provided. Four novel orthogonal low-complexity 8-point DCT approximations are obtained by solving a multicriteria optimization problem. The optimal 8-point transforms are scaled to lengths 16 and 32 while keeping the arithmetic complexity low. The proposed methods are assessed by proximity and coding measures with respect to the exact DCT. Image and video coding experiments hardware realization are performed. The novel transforms perform close to or outperform the current state-of-the-art DCT approximations.

A Multiparametric Class of Low-complexity Transforms for Image and Video Coding

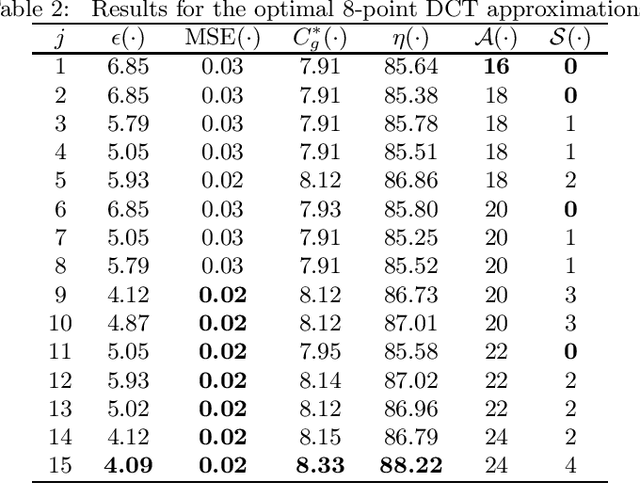
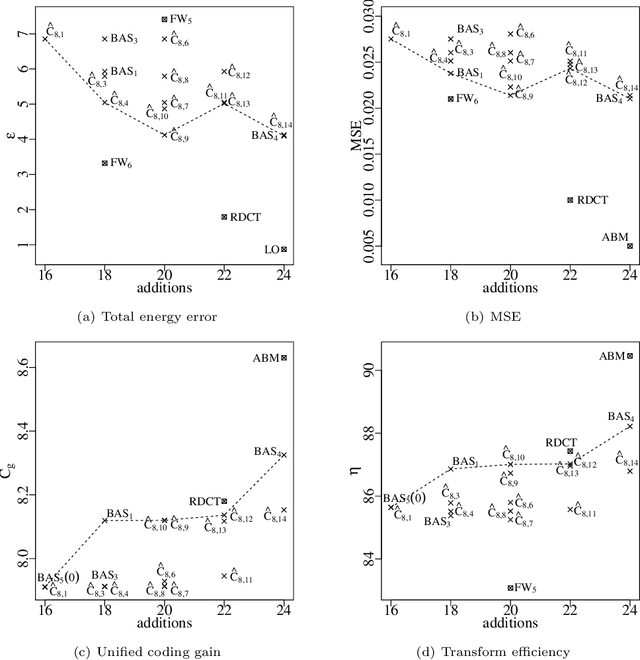
Discrete transforms play an important role in many signal processing applications, and low-complexity alternatives for classical transforms became popular in recent years. Particularly, the discrete cosine transform (DCT) has proven to be convenient for data compression, being employed in well-known image and video coding standards such as JPEG, H.264, and the recent high efficiency video coding (HEVC). In this paper, we introduce a new class of low-complexity 8-point DCT approximations based on a series of works published by Bouguezel, Ahmed and Swamy. Also, a multiparametric fast algorithm that encompasses both known and novel transforms is derived. We select the best-performing DCT approximations after solving a multicriteria optimization problem, and submit them to a scaling method for obtaining larger size transforms. We assess these DCT approximations in both JPEG-like image compression and video coding experiments. We show that the optimal DCT approximations present compelling results in terms of coding efficiency and image quality metrics, and require only few addition or bit-shifting operations, being suitable for low-complexity and low-power systems.