2-D Rayleigh Autoregressive Moving Average Model for SAR Image Modeling

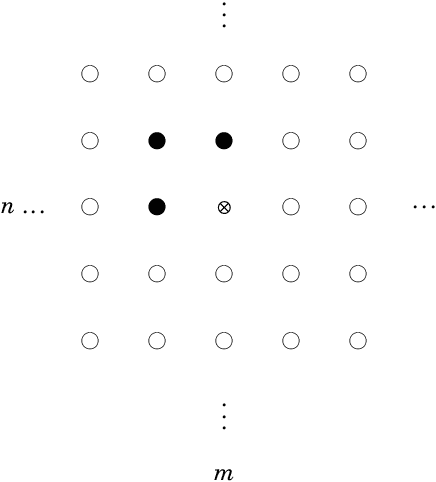
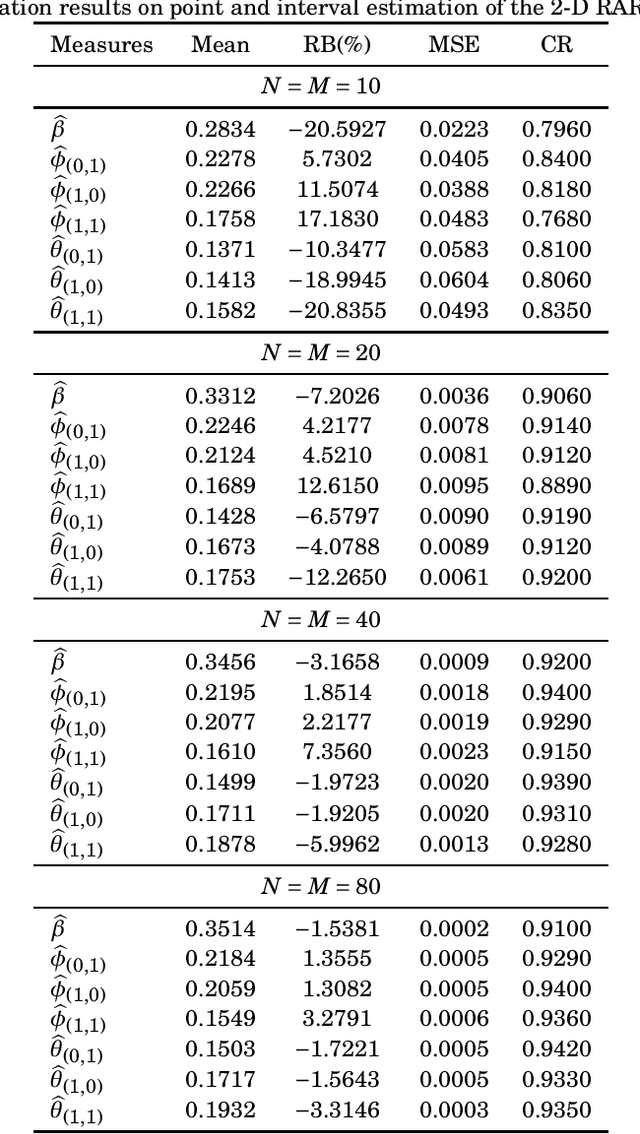
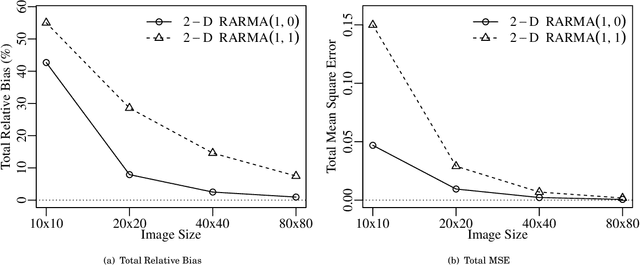
Two-dimensional (2-D) autoregressive moving average (ARMA) models are commonly applied to describe real-world image data, usually assuming Gaussian or symmetric noise. However, real-world data often present non-Gaussian signals, with asymmetrical distributions and strictly positive values. In particular, SAR images are known to be well characterized by the Rayleigh distribution. In this context, the ARMA model tailored for 2-D Rayleigh-distributed data is introduced -- the 2-D RARMA model. The 2-D RARMA model is derived and conditional likelihood inferences are discussed. The proposed model was submitted to extensive Monte Carlo simulations to evaluate the performance of the conditional maximum likelihood estimators. Moreover, in the context of SAR image processing, two comprehensive numerical experiments were performed comparing anomaly detection and image modeling results of the proposed model with traditional 2-D ARMA models and competing methods in the literature.

Improved Point Estimation for the Rayleigh Regression Model

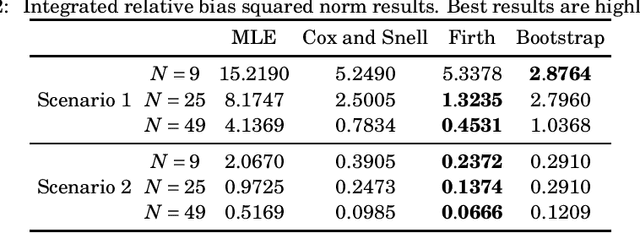
The Rayleigh regression model was recently proposed for modeling amplitude values of synthetic aperture radar (SAR) image pixels. However, inferences from such model are based on the maximum likelihood estimators, which can be biased for small signal lengths. The Rayleigh regression model for SAR images often takes into account small pixel windows, which may lead to inaccurate results. In this letter, we introduce bias-adjusted estimators tailored for the Rayleigh regression model based on: (i) the Cox and Snell's method; (ii) the Firth's scheme; and (iii) the parametric bootstrap method. We present numerical experiments considering synthetic and actual SAR data sets. The bias-adjusted estimators yield nearly unbiased estimates and accurate modeling results.

Robust Rayleigh Regression Method for SAR Image Processing in Presence of Outliers

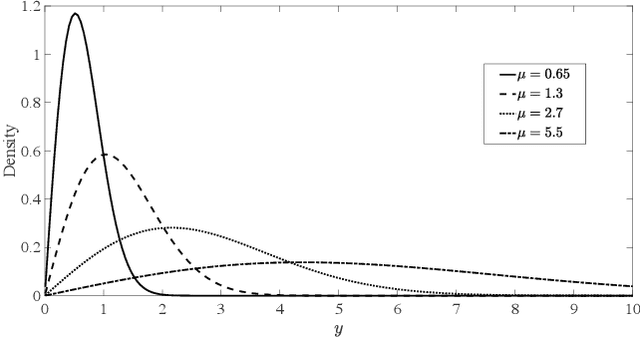
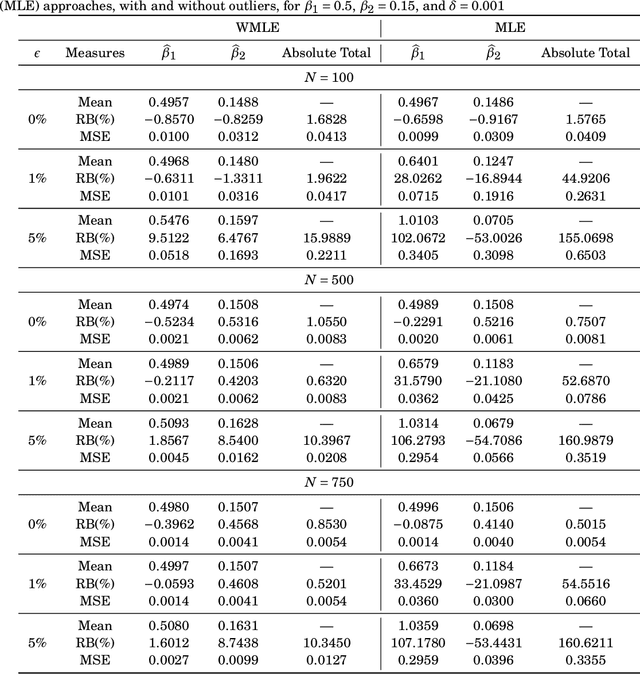
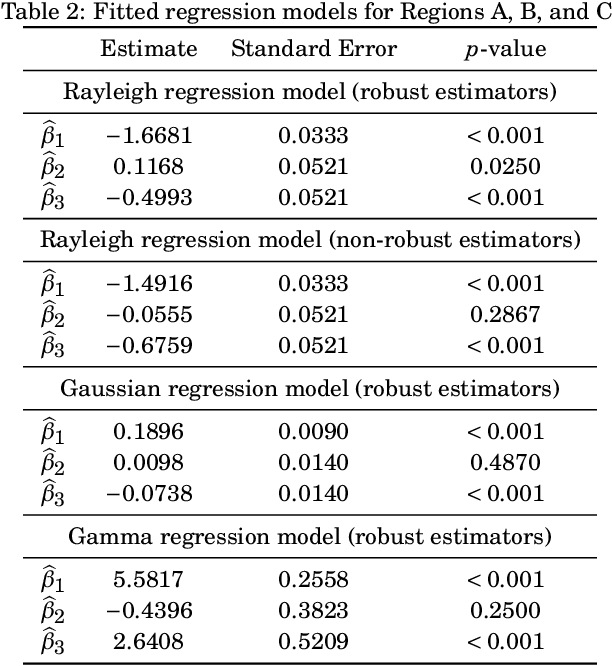
The presence of outliers (anomalous values) in synthetic aperture radar (SAR) data and the misspecification in statistical image models may result in inaccurate inferences. To avoid such issues, the Rayleigh regression model based on a robust estimation process is proposed as a more realistic approach to model this type of data. This paper aims at obtaining Rayleigh regression model parameter estimators robust to the presence of outliers. The proposed approach considered the weighted maximum likelihood method and was submitted to numerical experiments using simulated and measured SAR images. Monte Carlo simulations were employed for the numerical assessment of the proposed robust estimator performance in finite signal lengths, their sensitivity to outliers, and the breakdown point. For instance, the non-robust estimators show a relative bias value $65$-fold larger than the results provided by the robust approach in corrupted signals. In terms of sensitivity analysis and break down point, the robust scheme resulted in a reduction of about $96\%$ and $10\%$, respectively, in the mean absolute value of both measures, in compassion to the non-robust estimators. Moreover, two SAR data sets were used to compare the ground type and anomaly detection results of the proposed robust scheme with competing methods in the literature.

Signal Detection and Inference Based on the Beta Binomial Autoregressive Moving Average Model

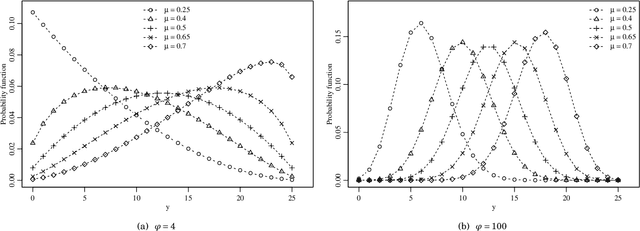
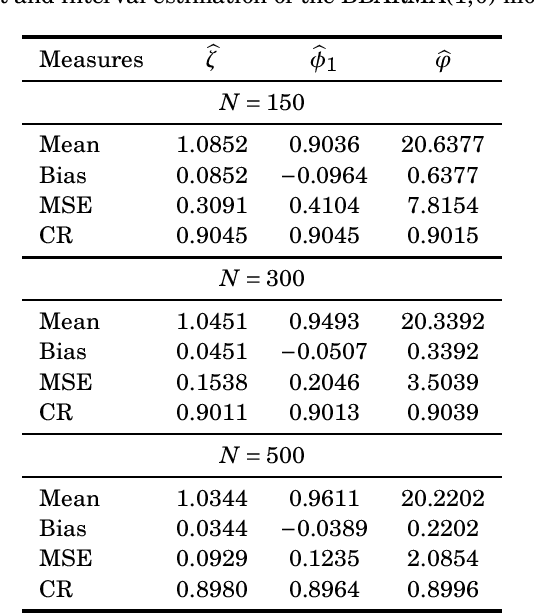
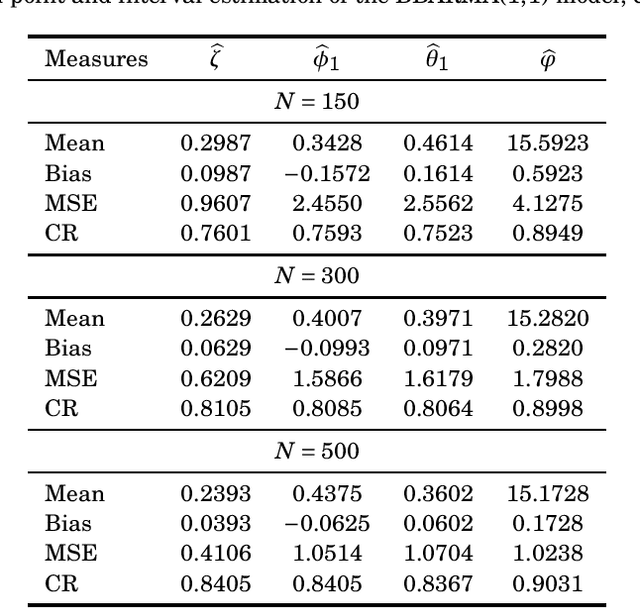
This paper proposes the beta binomial autoregressive moving average model (BBARMA) for modeling quantized amplitude data and bounded count data. The BBARMA model estimates the conditional mean of a beta binomial distributed variable observed over the time by a dynamic structure including: (i) autoregressive and moving average terms; (ii) a set of regressors; and (iii) a link function. Besides introducing the new model, we develop parameter estimation, detection tools, an out-of-signal forecasting scheme, and diagnostic measures. In particular, we provide closed-form expressions for the conditional score vector and the conditional information matrix. The proposed model was submitted to extensive Monte Carlo simulations in order to evaluate the performance of the conditional maximum likelihood estimators and of the proposed detector. The derived detector outperforms the usual ARMA- and Gaussian-based detectors for sinusoidal signal detection. We also presented an experiment for modeling and forecasting the monthly number of rainy days in Recife, Brazil.

Prediction Intervals in the Beta Autoregressive Moving Average Model

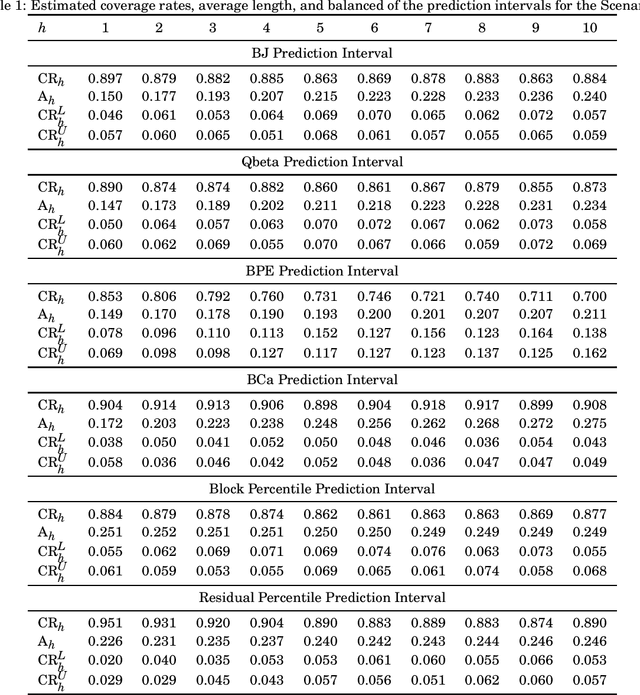
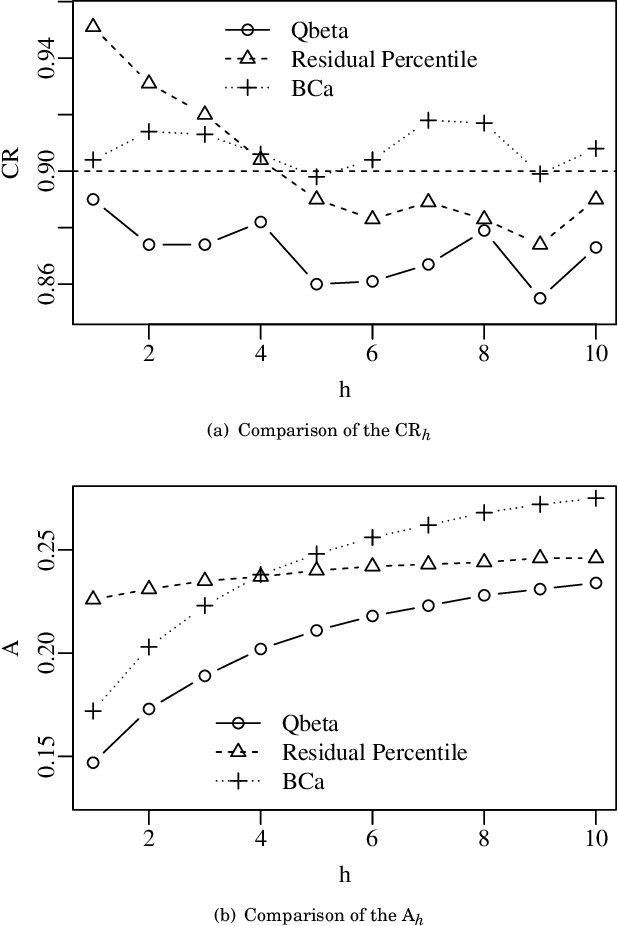
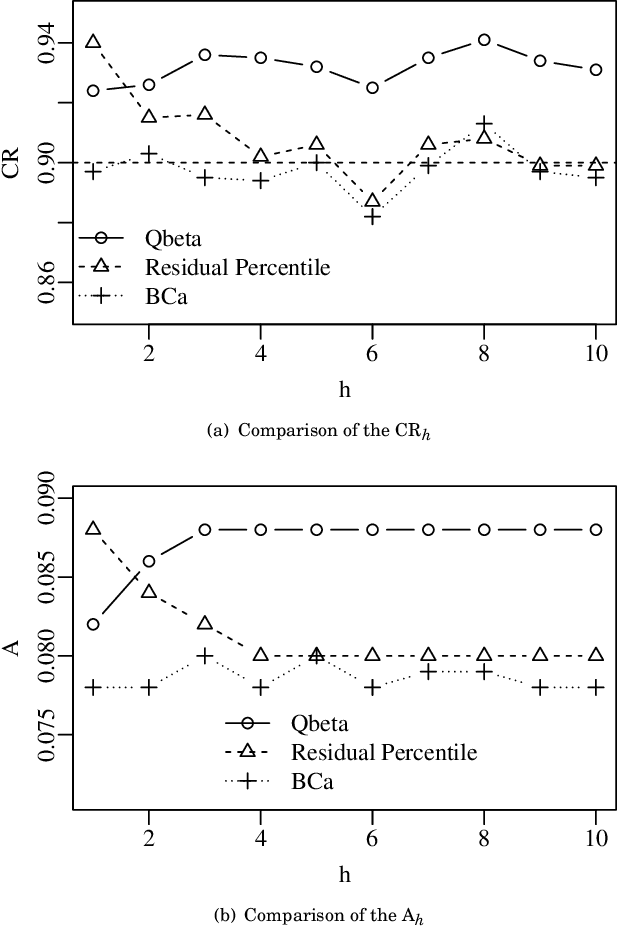
In this paper, we propose five prediction intervals for the beta autoregressive moving average model. This model is suitable for modeling and forecasting variables that assume values in the interval $(0,1)$. Two of the proposed prediction intervals are based on approximations considering the normal distribution and the quantile function of the beta distribution. We also consider bootstrap-based prediction intervals, namely: (i) bootstrap prediction errors (BPE) interval; (ii) bias-corrected and acceleration (BCa) prediction interval; and (iii) percentile prediction interval based on the quantiles of the bootstrap-predicted values for two different bootstrapping schemes. The proposed prediction intervals were evaluated according to Monte Carlo simulations. The BCa prediction interval offered the best performance among the evaluated intervals, showing lower coverage rate distortion and small average length. We applied our methodology for predicting the water level of the Cantareira water supply system in S\~ao Paulo, Brazil.

Wavelength-Resolution SAR Ground Scene Prediction Based on Image Stack

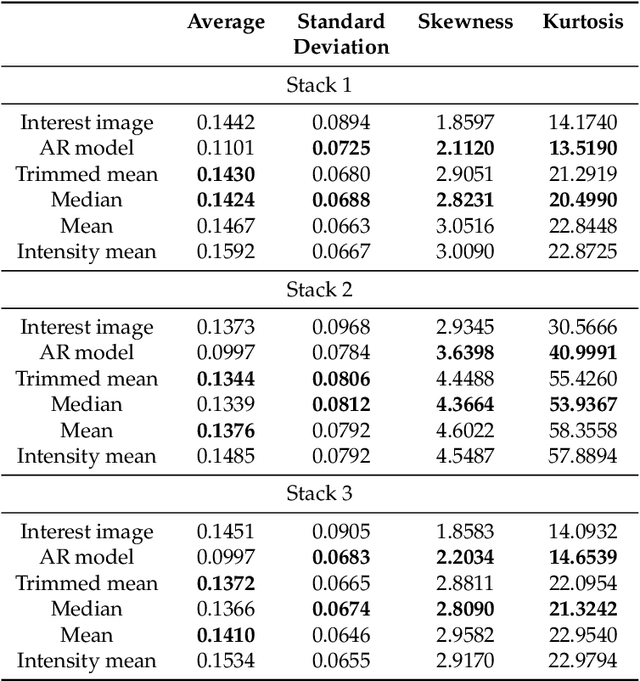
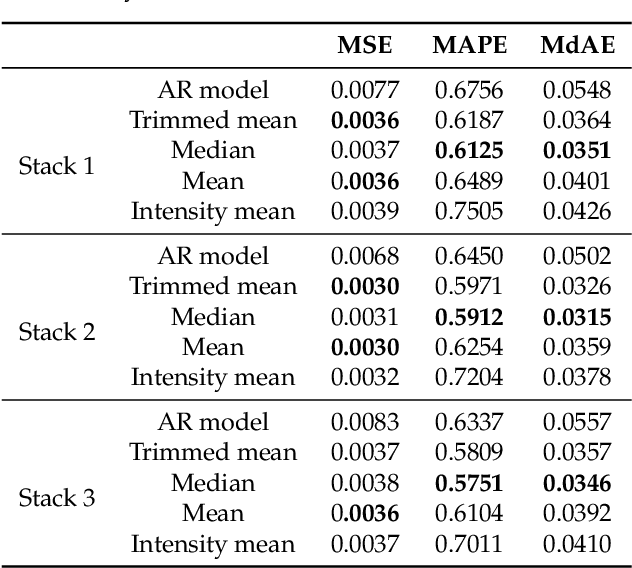
This paper presents five different statistical methods for ground scene prediction (GSP) in wavelength-resolution synthetic aperture radar (SAR) images. The GSP image can be used as a reference image in a change detection algorithm yielding a high probability of detection and low false alarm rate. The predictions are based on image stacks, which are composed of images from the same scene acquired at different instants with the same flight geometry. The considered methods for obtaining the ground scene prediction include (i) autoregressive models; (ii) trimmed mean; (iii) median; (iv) intensity mean; and (v) mean. It is expected that the predicted image presents the true ground scene without change and preserves the ground backscattering pattern. The study indicate that the the median method provided the most accurate representation of the true ground. To show the applicability of the GSP, a change detection algorithm was considered using the median ground scene as a reference image. As a result, the median method displayed the probability of detection of $97\%$ and a false alarm rate of 0.11/km$^2, when considering military vehicles concealed in a forest.

Rayleigh Regression Model for Ground Type Detection in SAR Imagery

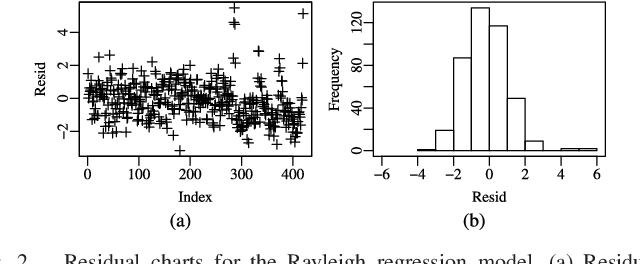
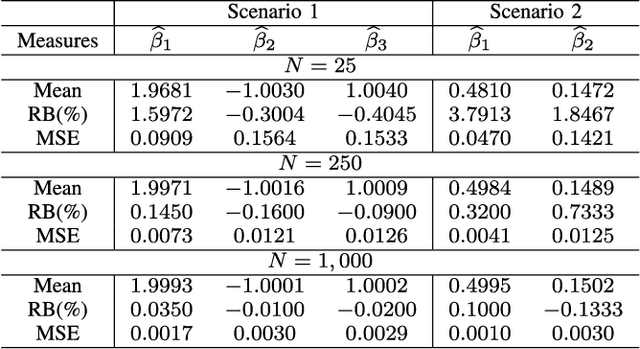
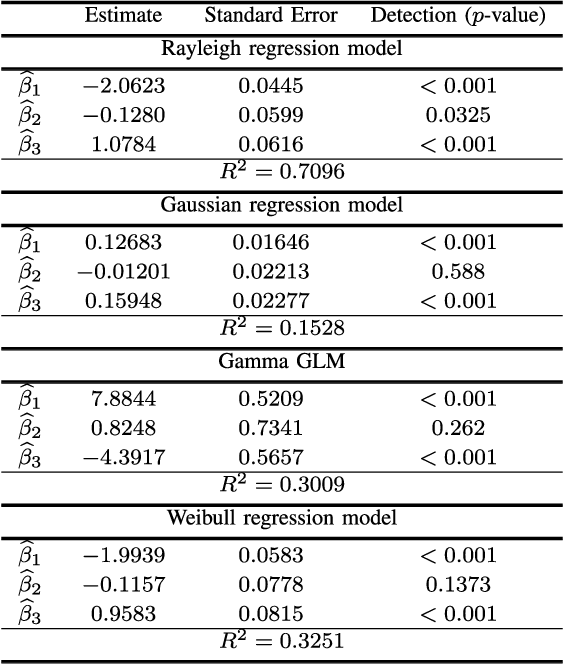
This letter proposes a regression model for nonnegative signals. The proposed regression estimates the mean of Rayleigh distributed signals by a structure which includes a set of regressors and a link function. For the proposed model, we present: (i)~parameter estimation; (ii)~large data record results; and (iii)~a detection technique. In this letter, we present closed-form expressions for the score vector and Fisher information matrix. The proposed model is submitted to extensive Monte Carlo simulations and to measured data. The Monte Carlo simulations are used to evaluate the performance of maximum likelihood estimators. Also, an application is performed comparing the detection results of the proposed model with Gaussian-, Gamma-, and Weibull-based regression models in SAR images.

Autoregressive Model for Multi-Pass SAR Change Detection Based on Image Stacks

Change detection is an important synthetic aperture radar (SAR) application, usually used to detect changes on the ground scene measurements in different moments in time. Traditionally, change detection algorithm (CDA) is mainly designed for two synthetic aperture radar (SAR) images retrieved at different instants. However, more images can be used to improve the algorithms performance, witch emerges as a research topic on SAR change detection. Image stack information can be treated as a data series over time and can be modeled by autoregressive (AR) models. Thus, we present some initial findings on SAR change detection based on image stack considering AR models. Applying AR model for each pixel position in the image stack, we obtained an estimated image of the ground scene which can be used as a reference image for CDA. The experimental results reveal that ground scene estimates by the AR models is accurate and can be used for change detection applications.