Robust Rayleigh Regression Method for SAR Image Processing in Presence of Outliers
Paper and Code
Jul 29, 2022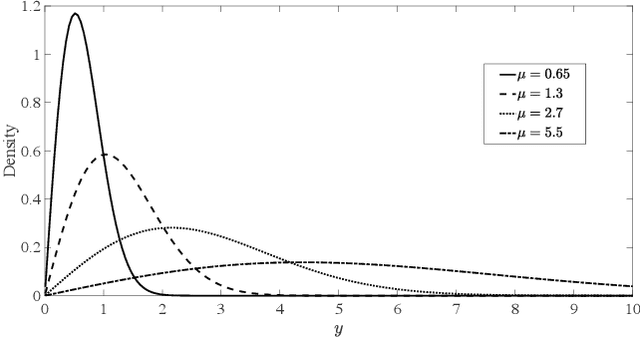
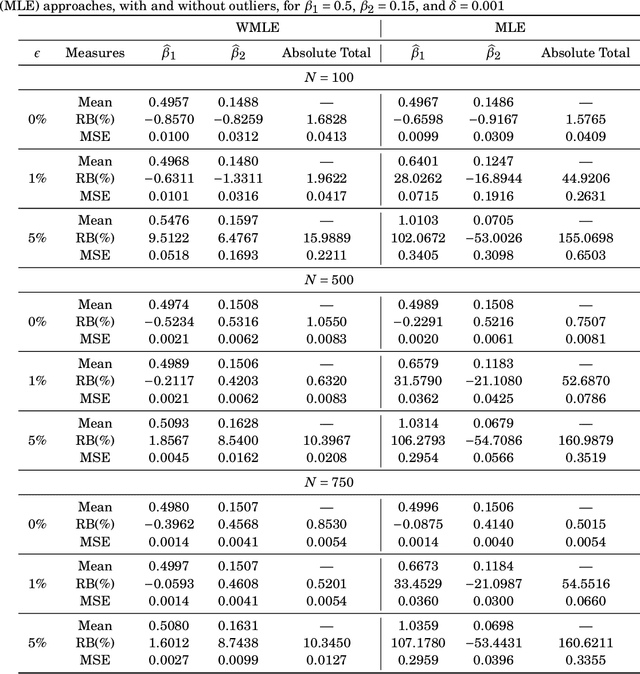

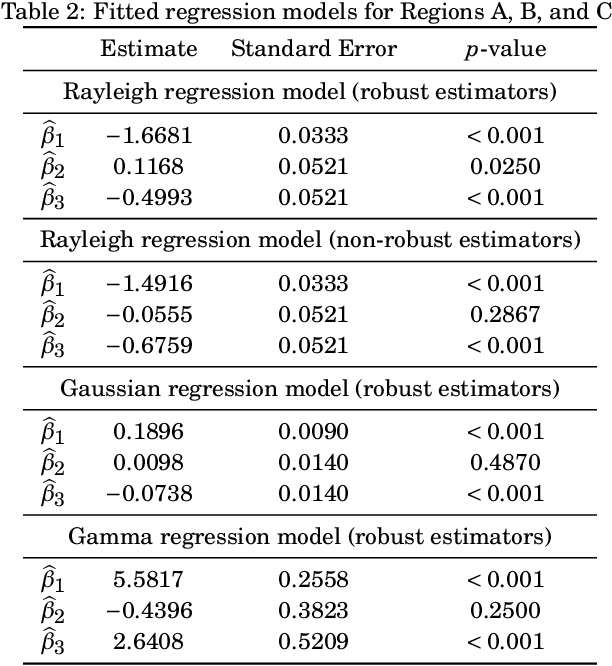
The presence of outliers (anomalous values) in synthetic aperture radar (SAR) data and the misspecification in statistical image models may result in inaccurate inferences. To avoid such issues, the Rayleigh regression model based on a robust estimation process is proposed as a more realistic approach to model this type of data. This paper aims at obtaining Rayleigh regression model parameter estimators robust to the presence of outliers. The proposed approach considered the weighted maximum likelihood method and was submitted to numerical experiments using simulated and measured SAR images. Monte Carlo simulations were employed for the numerical assessment of the proposed robust estimator performance in finite signal lengths, their sensitivity to outliers, and the breakdown point. For instance, the non-robust estimators show a relative bias value $65$-fold larger than the results provided by the robust approach in corrupted signals. In terms of sensitivity analysis and break down point, the robust scheme resulted in a reduction of about $96\%$ and $10\%$, respectively, in the mean absolute value of both measures, in compassion to the non-robust estimators. Moreover, two SAR data sets were used to compare the ground type and anomaly detection results of the proposed robust scheme with competing methods in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge