Signal Detection and Inference Based on the Beta Binomial Autoregressive Moving Average Model
Paper and Code
Jul 29, 2022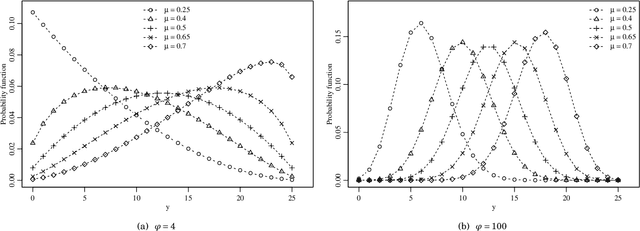
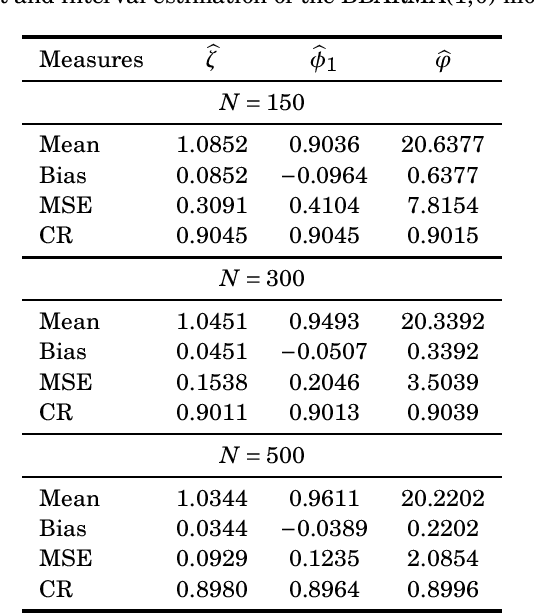
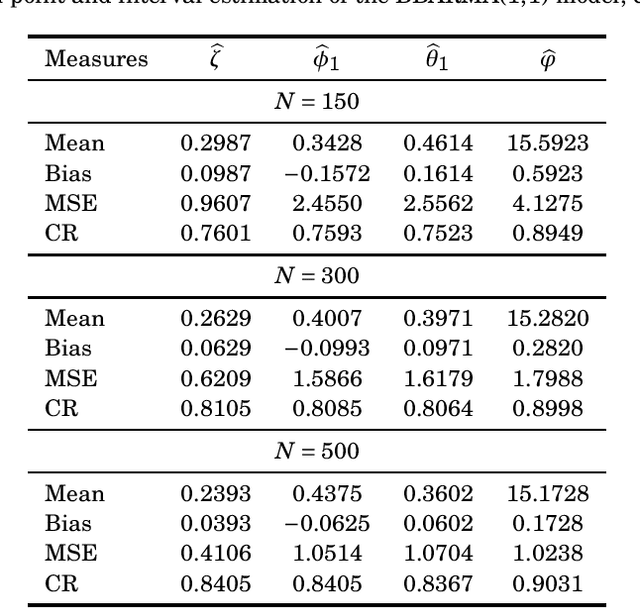

This paper proposes the beta binomial autoregressive moving average model (BBARMA) for modeling quantized amplitude data and bounded count data. The BBARMA model estimates the conditional mean of a beta binomial distributed variable observed over the time by a dynamic structure including: (i) autoregressive and moving average terms; (ii) a set of regressors; and (iii) a link function. Besides introducing the new model, we develop parameter estimation, detection tools, an out-of-signal forecasting scheme, and diagnostic measures. In particular, we provide closed-form expressions for the conditional score vector and the conditional information matrix. The proposed model was submitted to extensive Monte Carlo simulations in order to evaluate the performance of the conditional maximum likelihood estimators and of the proposed detector. The derived detector outperforms the usual ARMA- and Gaussian-based detectors for sinusoidal signal detection. We also presented an experiment for modeling and forecasting the monthly number of rainy days in Recife, Brazil.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge