2-D Rayleigh Autoregressive Moving Average Model for SAR Image Modeling
Paper and Code
Aug 07, 2022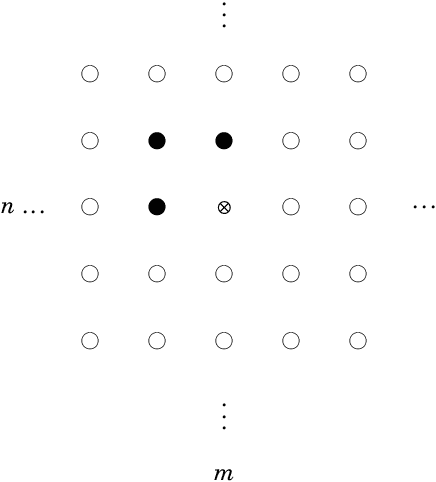

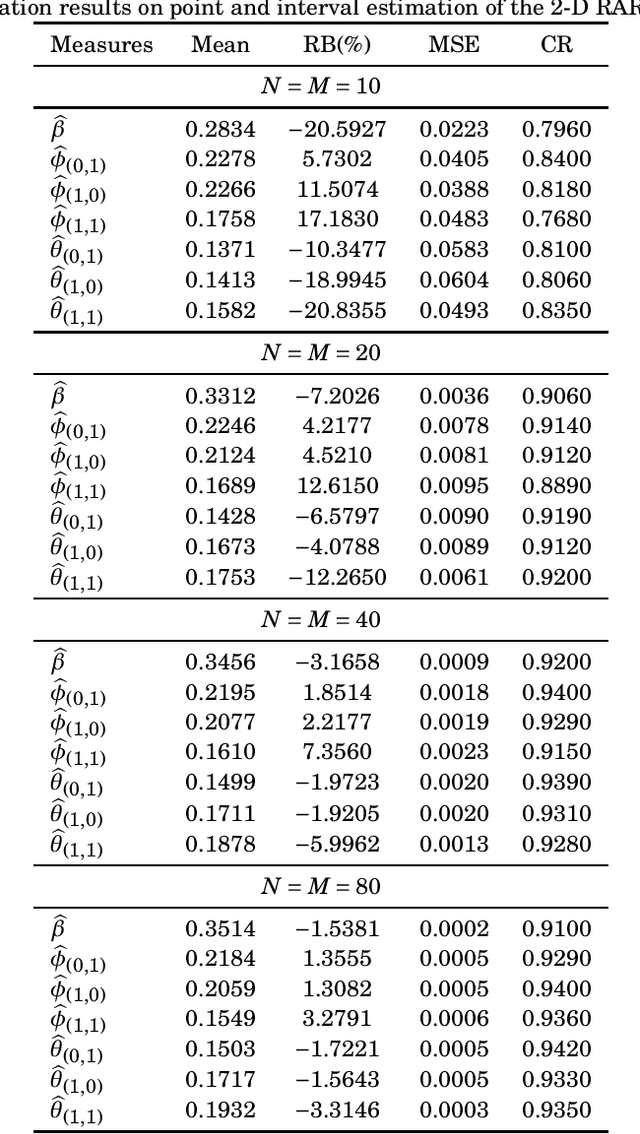
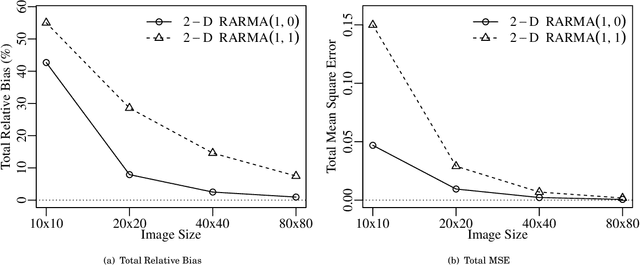
Two-dimensional (2-D) autoregressive moving average (ARMA) models are commonly applied to describe real-world image data, usually assuming Gaussian or symmetric noise. However, real-world data often present non-Gaussian signals, with asymmetrical distributions and strictly positive values. In particular, SAR images are known to be well characterized by the Rayleigh distribution. In this context, the ARMA model tailored for 2-D Rayleigh-distributed data is introduced -- the 2-D RARMA model. The 2-D RARMA model is derived and conditional likelihood inferences are discussed. The proposed model was submitted to extensive Monte Carlo simulations to evaluate the performance of the conditional maximum likelihood estimators. Moreover, in the context of SAR image processing, two comprehensive numerical experiments were performed comparing anomaly detection and image modeling results of the proposed model with traditional 2-D ARMA models and competing methods in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge