Regression Model for Speckled Data with Extremely Variability

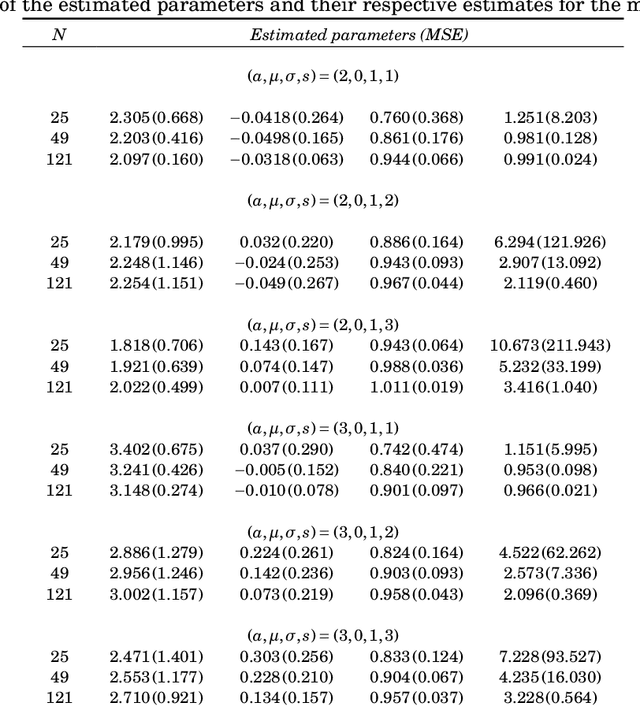
Synthetic aperture radar (SAR) is an efficient and widely used remote sensing tool. However, data extracted from SAR images are contaminated with speckle, which precludes the application of techniques based on the assumption of additive and normally distributed noise. One of the most successful approaches to describing such data is the multiplicative model, where intensities can follow a variety of distributions with positive support. The $\mathcal{G}^0_I$ model is among the most successful ones. Although several estimation methods for the $\mathcal{G}^0_I$ parameters have been proposed, there is no work exploring a regression structure for this model. Such a structure could allow us to infer unobserved values from available ones. In this work, we propose a $\mathcal{G}^0_I$ regression model and use it to describe the influence of intensities from other polarimetric channels. We derive some theoretical properties for the new model: Fisher information matrix, residual measures, and influential tools. Maximum likelihood point and interval estimation methods are proposed and evaluated by Monte Carlo experiments. Results from simulated and actual data show that the new model can be helpful for SAR image analysis.

The Gamma Generalized Normal Distribution: A Descriptor of SAR Imagery

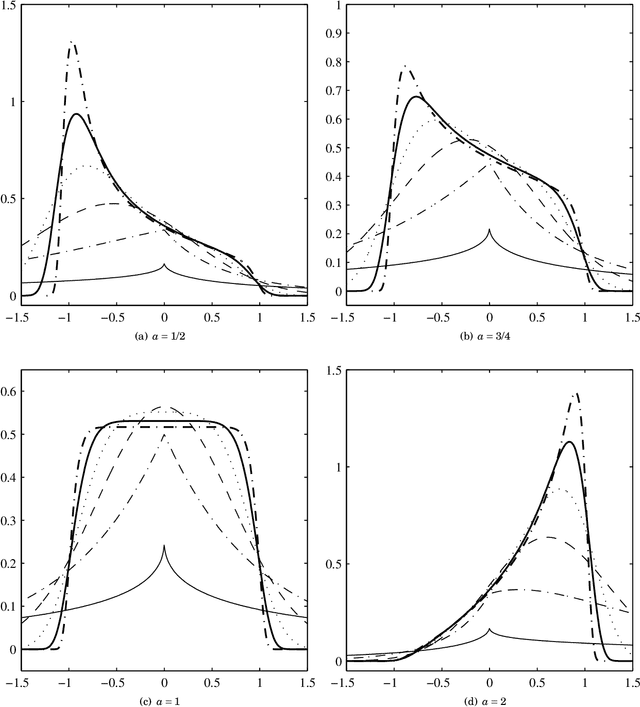
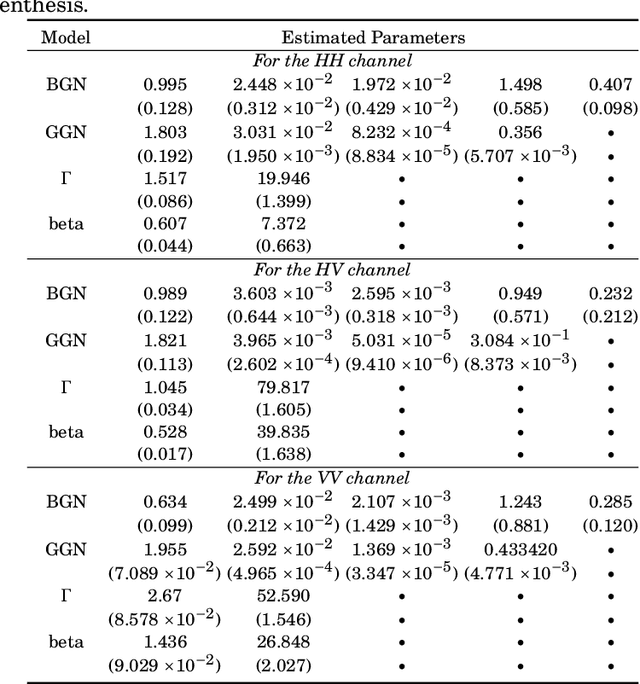
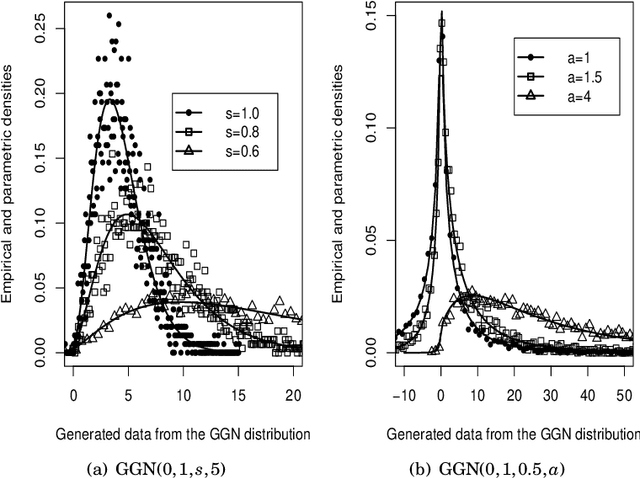
We propose a new four-parameter distribution for modeling synthetic aperture radar (SAR) imagery named the gamma generalized normal (GGN) by combining the gamma and generalized normal distributions. A mathematical characterization of the new distribution is provided by identifying the limit behavior and by calculating the density and moment expansions. The GGN model performance is evaluated on both synthetic and actual data and, for that, maximum likelihood estimation and random number generation are discussed. The proposed distribution is compared with the beta generalized normal distribution (BGN), which has already shown to appropriately represent SAR imagery. The performance of these two distributions are measured by means of statistics which provide evidence that the GGN can outperform the BGN distribution in some contexts.

Beta Generalized Normal Distribution with an Application for SAR Image Processing

We introduce the beta generalized normal distribution which is obtained by compounding the beta and generalized normal [Nadarajah, S., A generalized normal distribution, \emph{Journal of Applied Statistics}. 32, 685--694, 2005] distributions. The new model includes as sub-models the beta normal, beta Laplace, normal, and Laplace distributions. The shape of the new distribution is quite flexible, specially the skewness and the tail weights, due to two additional parameters. We obtain general expansions for the moments. The estimation of the parameters is investigated by maximum likelihood. We also proposed a random number generator for the new distribution. Actual synthetic aperture radar were analyzed and modeled after the new distribution. Results could outperform the $\mathcal{G}^0$, $\mathcal{K}$, and $\Gamma$ distributions in several scenarios.