Optimal Direct-Connect Topologies for Collective Communications

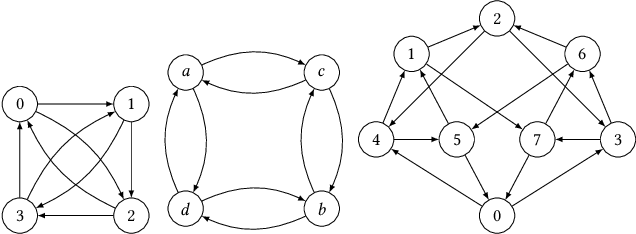
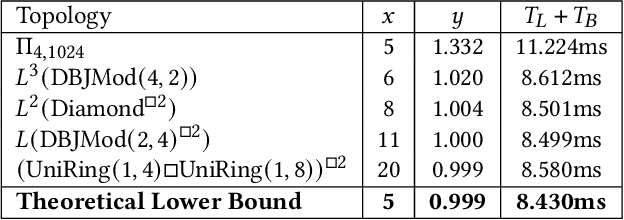
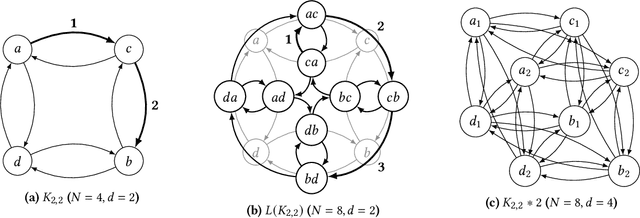
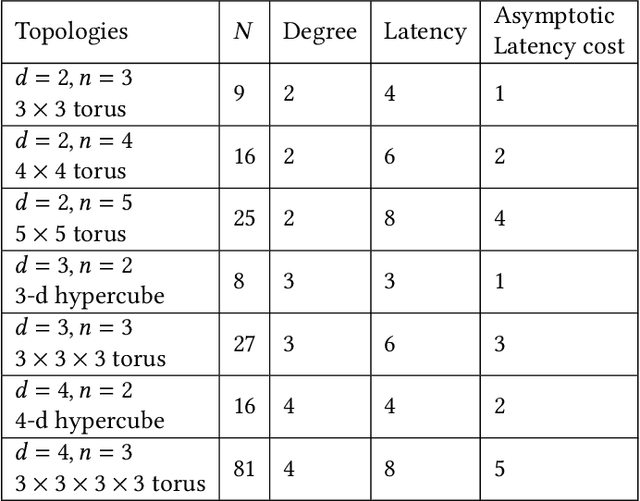
We consider the problem of distilling optimal network topologies for collective communications. We provide an algorithmic framework for constructing direct-connect topologies optimized for the latency-bandwidth tradeoff given a collective communication workload. Our algorithmic framework allows us to start from small base topologies and associated communication schedules and use a set of techniques that can be iteratively applied to derive much larger topologies and associated schedules. Our approach allows us to synthesize many different topologies and schedules for a given cluster size and degree constraint, and then identify the optimal topology for a given workload. We provide an analytical-model-based evaluation of the derived topologies and results on a small-scale optical testbed that uses patch panels for configuring a topology for the duration of an application's execution. We show that the derived topologies and schedules provide significant performance benefits over existing collective communications implementations.

Outlier Detection from Network Data with Subnetwork Interpretation

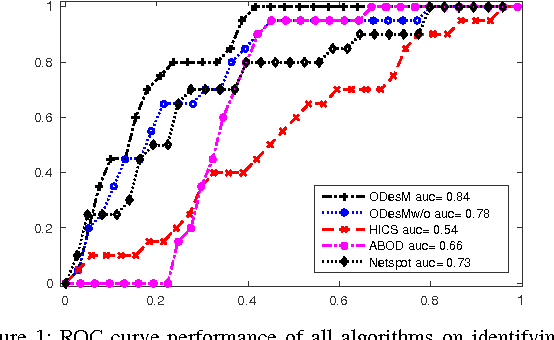
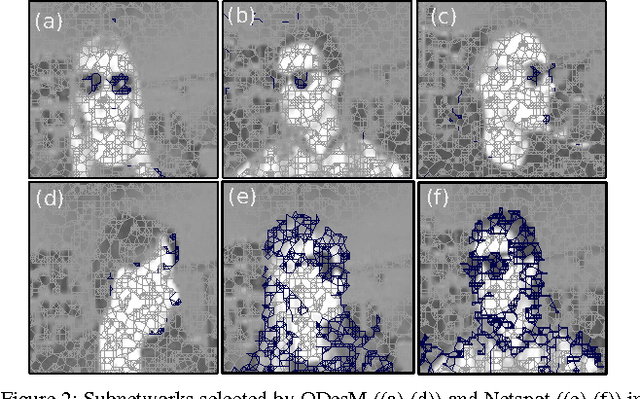
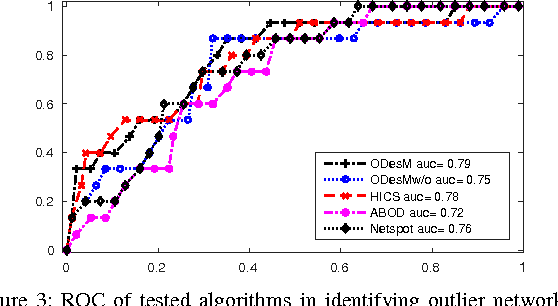
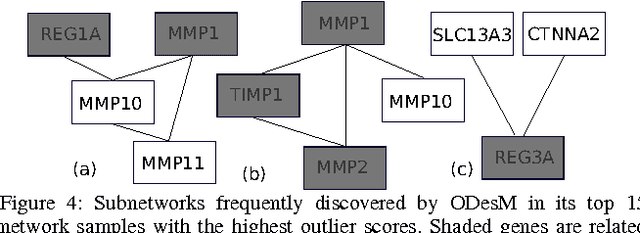
Detecting a small number of outliers from a set of data observations is always challenging. This problem is more difficult in the setting of multiple network samples, where computing the anomalous degree of a network sample is generally not sufficient. In fact, explaining why the network is exceptional, expressed in the form of subnetwork, is also equally important. In this paper, we develop a novel algorithm to address these two key problems. We treat each network sample as a potential outlier and identify subnetworks that mostly discriminate it from nearby regular samples. The algorithm is developed in the framework of network regression combined with the constraints on both network topology and L1-norm shrinkage to perform subnetwork discovery. Our method thus goes beyond subspace/subgraph discovery and we show that it converges to a global optimum. Evaluation on various real-world network datasets demonstrates that our algorithm not only outperforms baselines in both network and high dimensional setting, but also discovers highly relevant and interpretable local subnetworks, further enhancing our understanding of anomalous networks.