Phil Bachman
Decomposed Mutual Information Estimation for Contrastive Representation Learning
Jun 25, 2021



Abstract:Recent contrastive representation learning methods rely on estimating mutual information (MI) between multiple views of an underlying context. E.g., we can derive multiple views of a given image by applying data augmentation, or we can split a sequence into views comprising the past and future of some step in the sequence. Contrastive lower bounds on MI are easy to optimize, but have a strong underestimation bias when estimating large amounts of MI. We propose decomposing the full MI estimation problem into a sum of smaller estimation problems by splitting one of the views into progressively more informed subviews and by applying the chain rule on MI between the decomposed views. This expression contains a sum of unconditional and conditional MI terms, each measuring modest chunks of the total MI, which facilitates approximation via contrastive bounds. To maximize the sum, we formulate a contrastive lower bound on the conditional MI which can be approximated efficiently. We refer to our general approach as Decomposed Estimation of Mutual Information (DEMI). We show that DEMI can capture a larger amount of MI than standard non-decomposed contrastive bounds in a synthetic setting, and learns better representations in a vision domain and for dialogue generation.
Learning deep representations by mutual information estimation and maximization
Oct 03, 2018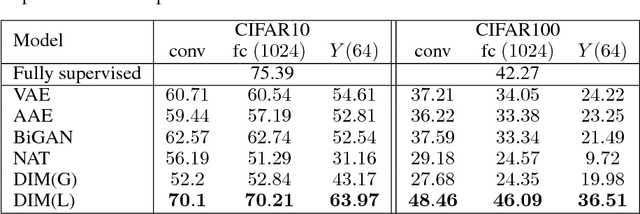
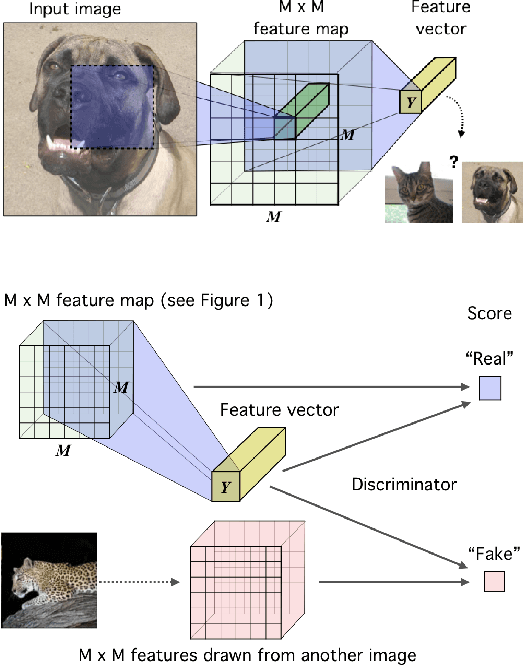
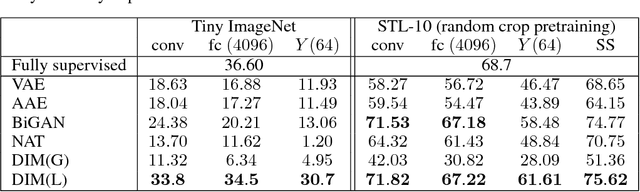
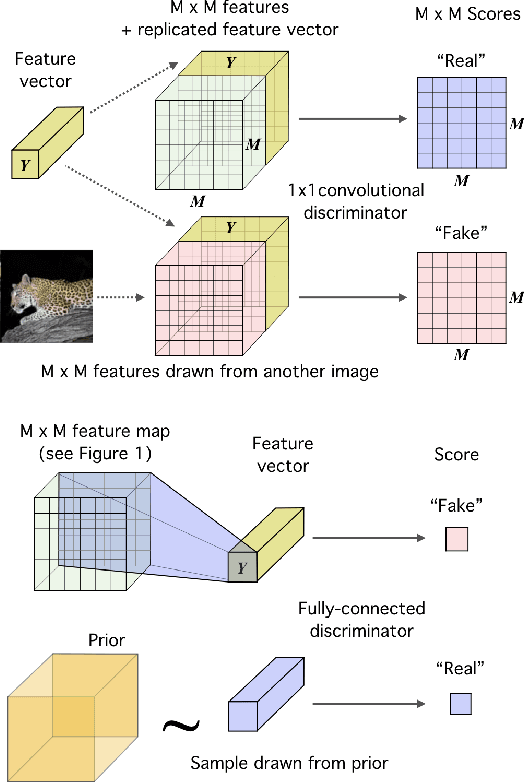
Abstract:In this work, we perform unsupervised learning of representations by maximizing mutual information between an input and the output of a deep neural network encoder. Importantly, we show that structure matters: incorporating knowledge about locality of the input to the objective can greatly influence a representation's suitability for downstream tasks. We further control characteristics of the representation by matching to a prior distribution adversarially. Our method, which we call Deep InfoMax (DIM), outperforms a number of popular unsupervised learning methods and competes with fully-supervised learning on several classification tasks. DIM opens new avenues for unsupervised learning of representations and is an important step towards flexible formulations of representation-learning objectives for specific end-goals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge