Benford's Law and First Letter of Word

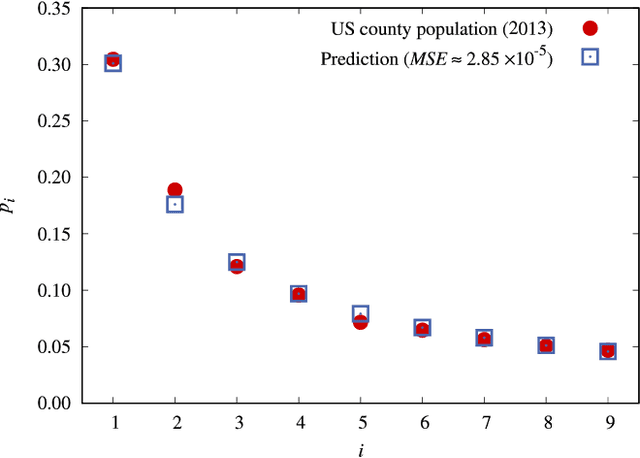
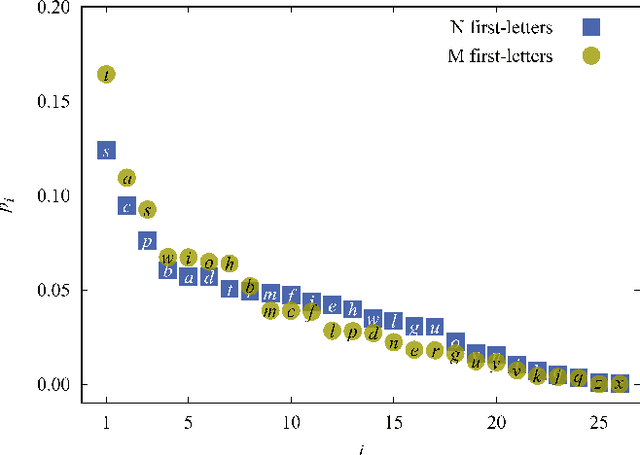
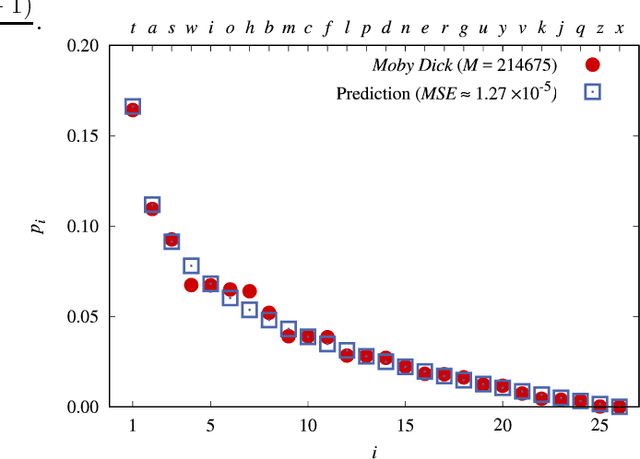
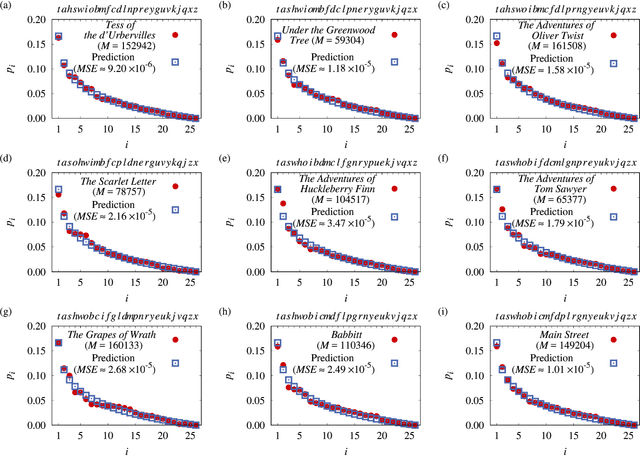
A universal First-Letter Law (FLL) is derived and described. It predicts the percentages of first letters for words in novels. The FLL is akin to Benford's law (BL) of first digits, which predicts the percentages of first digits in a data collection of numbers. Both are universal in the sense that FLL only depends on the numbers of letters in the alphabet, whereas BL only depends on the number of digits in the base of the number system. The existence of these types of universal laws appears counter-intuitive. Nonetheless both describe data very well. Relations to some earlier works are given. FLL predicts that an English author on the average starts about 16 out of 100 words with the English letter `t'. This is corroborated by data, yet an author can freely write anything. Fuller implications and the applicability of FLL remain for the future.

The Dependence of Frequency Distributions on Multiple Meanings of Words, Codes and Signs

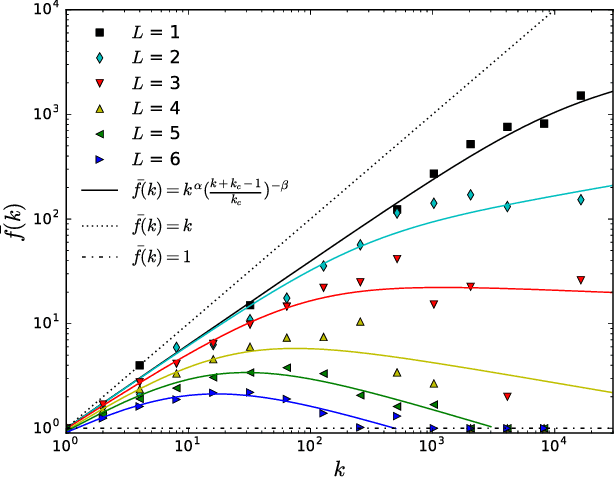
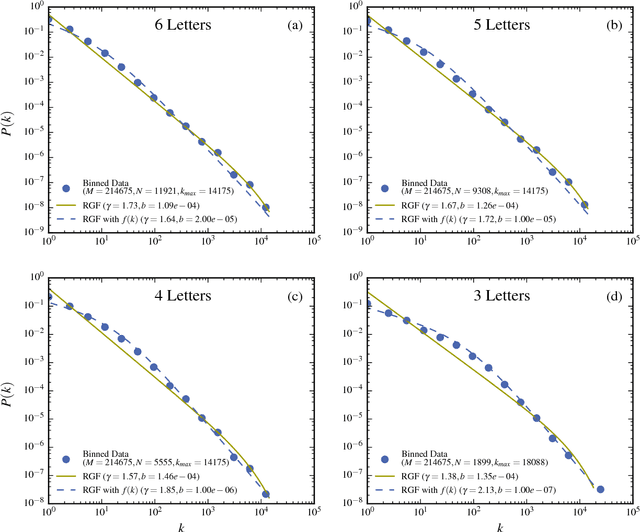
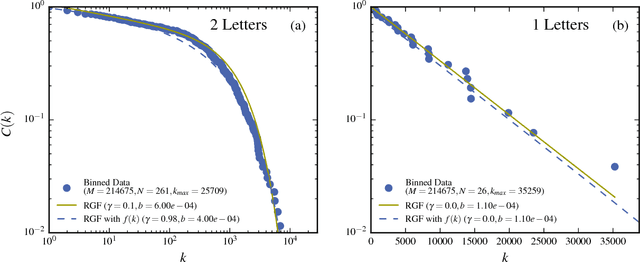
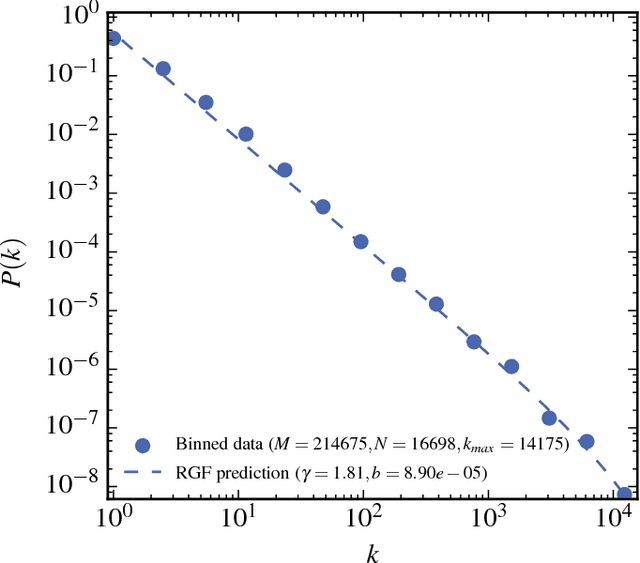
The dependence of the frequency distributions due to multiple meanings of words in a text is investigated by deleting letters. By coding the words with fewer letters the number of meanings per coded word increases. This increase is measured and used as an input in a predictive theory. For a text written in English, the word-frequency distribution is broad and fat-tailed, whereas if the words are only represented by their first letter the distribution becomes exponential. Both distribution are well predicted by the theory, as is the whole sequence obtained by consecutively representing the words by the first L=6,5,4,3,2,1 letters. Comparisons of texts written by Chinese characters and the same texts written by letter-codes are made and the similarity of the corresponding frequency-distributions are interpreted as a consequence of the multiple meanings of Chinese characters. This further implies that the difference of the shape for word-frequencies for an English text written by letters and a Chinese text written by Chinese characters is due to the coding and not to the language per se.

Maximum Entropy, Word-Frequency, Chinese Characters, and Multiple Meanings

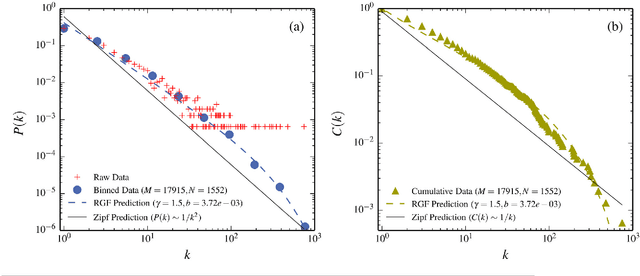
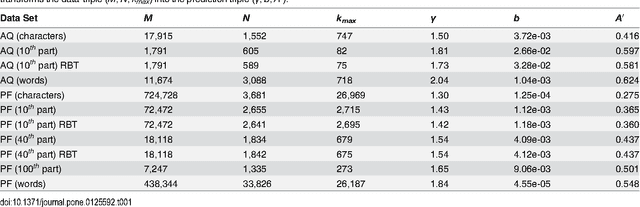
The word-frequency distribution of a text written by an author is well accounted for by a maximum entropy distribution, the RGF (random group formation)-prediction. The RGF-distribution is completely determined by the a priori values of the total number of words in the text (M), the number of distinct words (N) and the number of repetitions of the most common word (k_max). It is here shown that this maximum entropy prediction also describes a text written in Chinese characters. In particular it is shown that although the same Chinese text written in words and Chinese characters have quite differently shaped distributions, they are nevertheless both well predicted by their respective three a priori characteristic values. It is pointed out that this is analogous to the change in the shape of the distribution when translating a given text to another language. Another consequence of the RGF-prediction is that taking a part of a long text will change the input parameters (M, N, k_max) and consequently also the shape of the frequency distribution. This is explicitly confirmed for texts written in Chinese characters. Since the RGF-prediction has no system-specific information beyond the three a priori values (M, N, k_max), any specific language characteristic has to be sought in systematic deviations from the RGF-prediction and the measured frequencies. One such systematic deviation is identified and, through a statistical information theoretical argument and an extended RGF-model, it is proposed that this deviation is caused by multiple meanings of Chinese characters. The effect is stronger for Chinese characters than for Chinese words. The relation between Zipf's law, the Simon-model for texts and the present results are discussed.

A Paradoxical Property of the Monkey Book

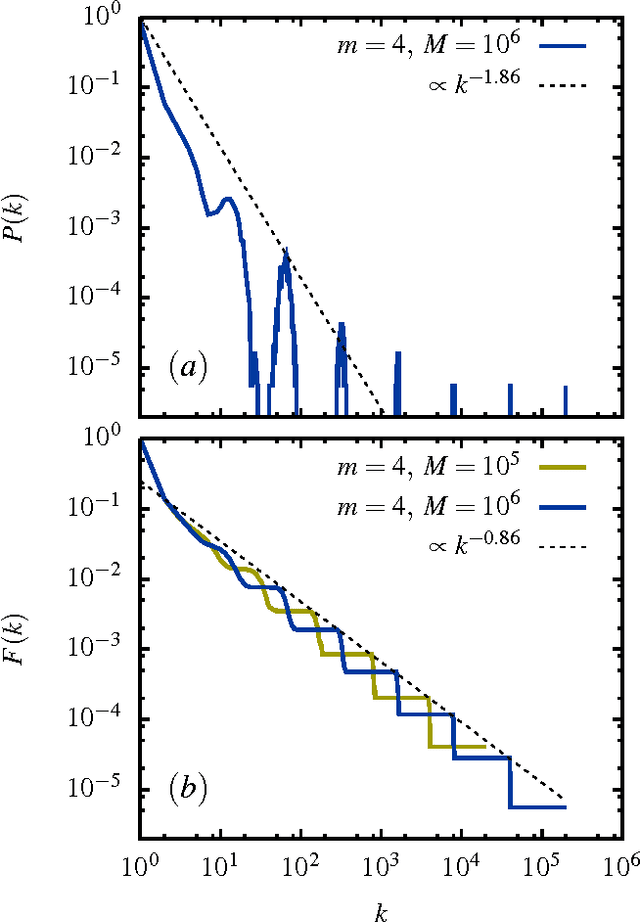
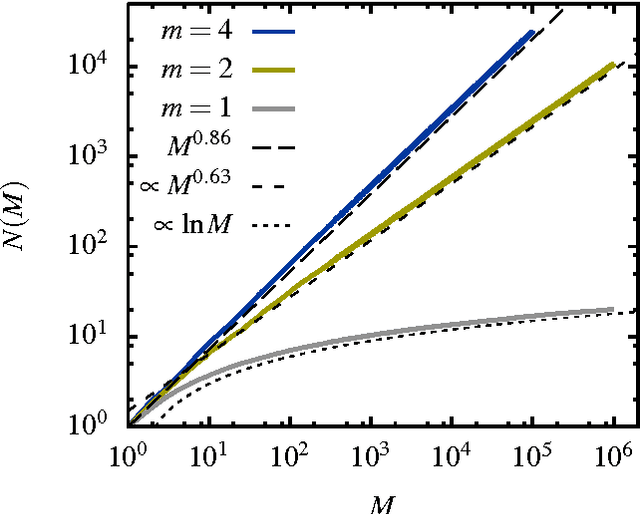
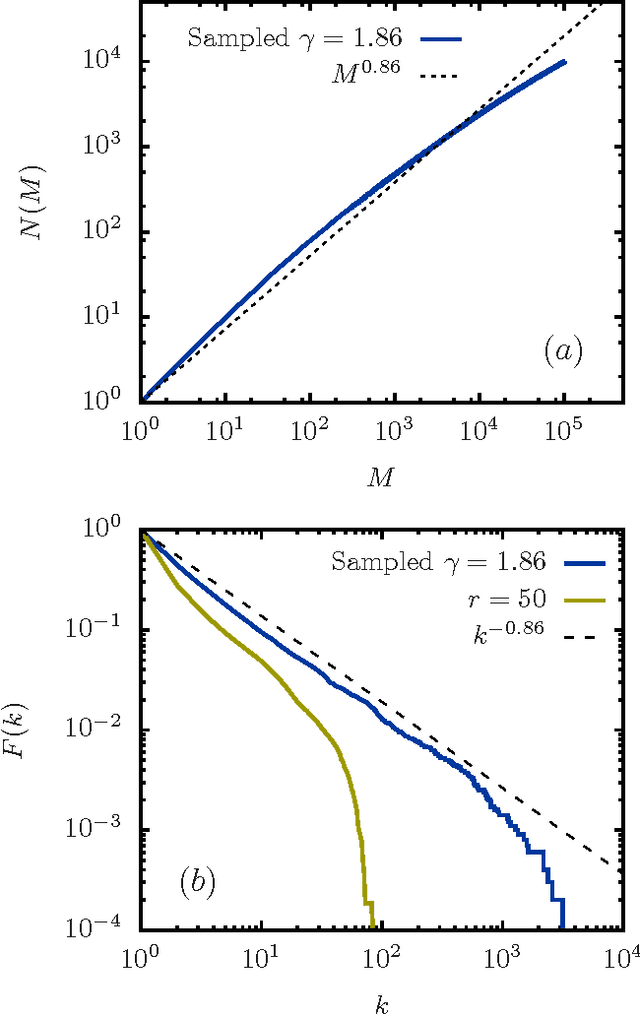
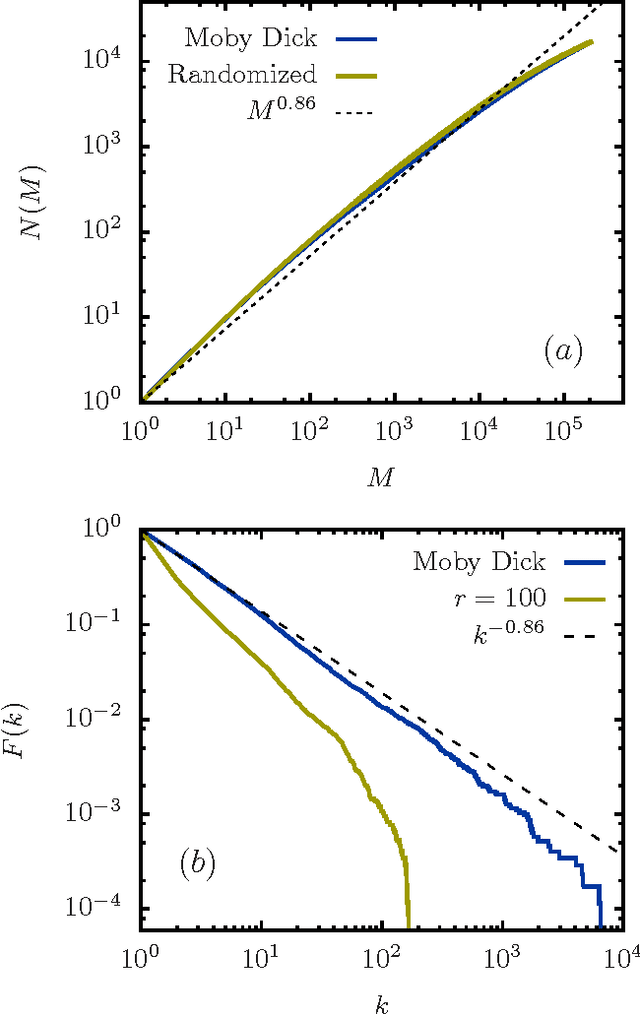
A "monkey book" is a book consisting of a random distribution of letters and blanks, where a group of letters surrounded by two blanks is defined as a word. We compare the statistics of the word distribution for a monkey book with the corresponding distribution for the general class of random books, where the latter are books for which the words are randomly distributed. It is shown that the word distribution statistics for the monkey book is different and quite distinct from a typical sampled book or real book. In particular the monkey book obeys Heaps' power law to an extraordinary good approximation, in contrast to the word distributions for sampled and real books, which deviate from Heaps' law in a characteristics way. The somewhat counter-intuitive conclusion is that a "monkey book" obeys Heaps' power law precisely because its word-frequency distribution is not a smooth power law, contrary to the expectation based on simple mathematical arguments that if one is a power law, so is the other.

The meta book and size-dependent properties of written language

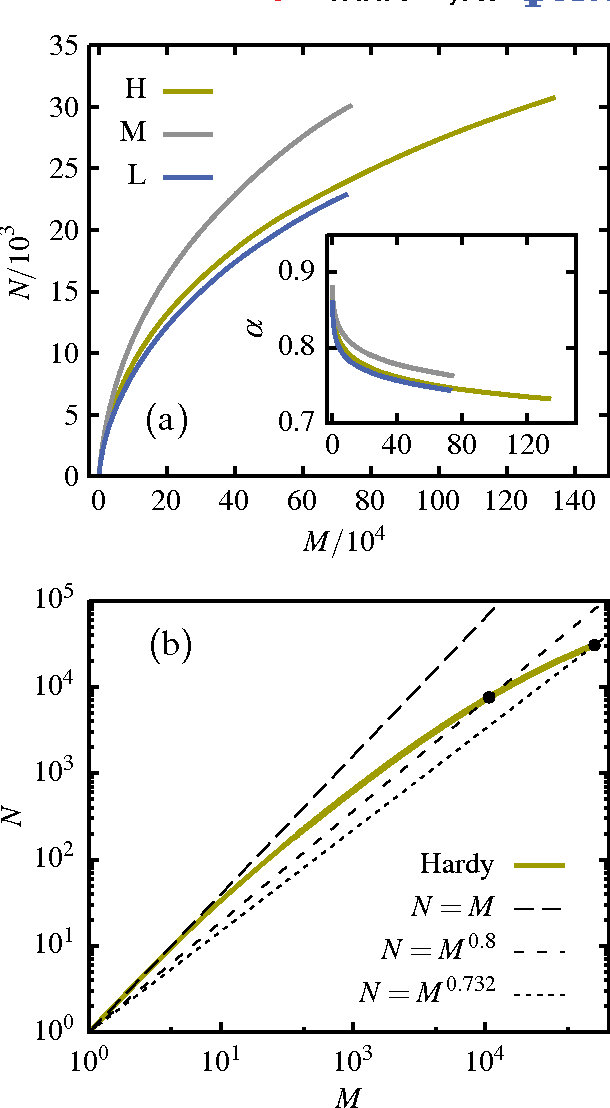
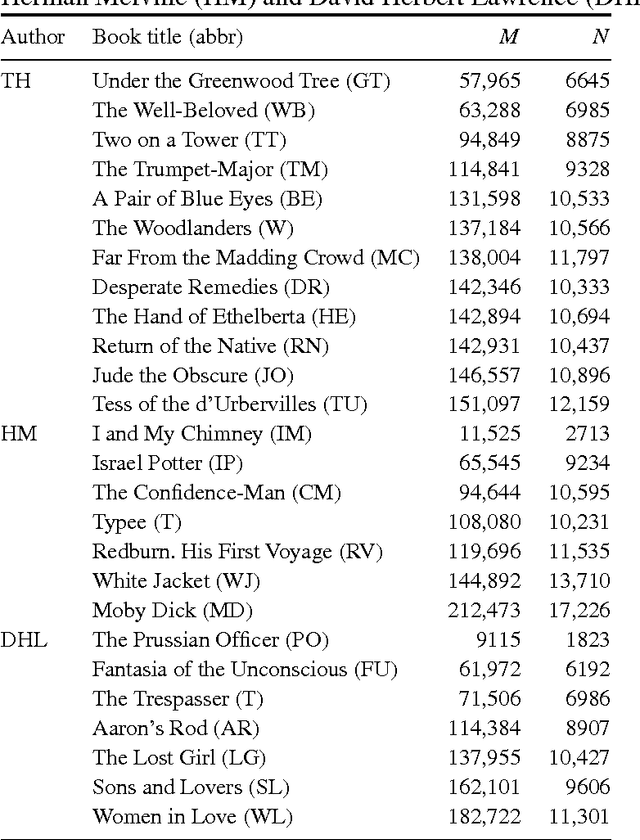
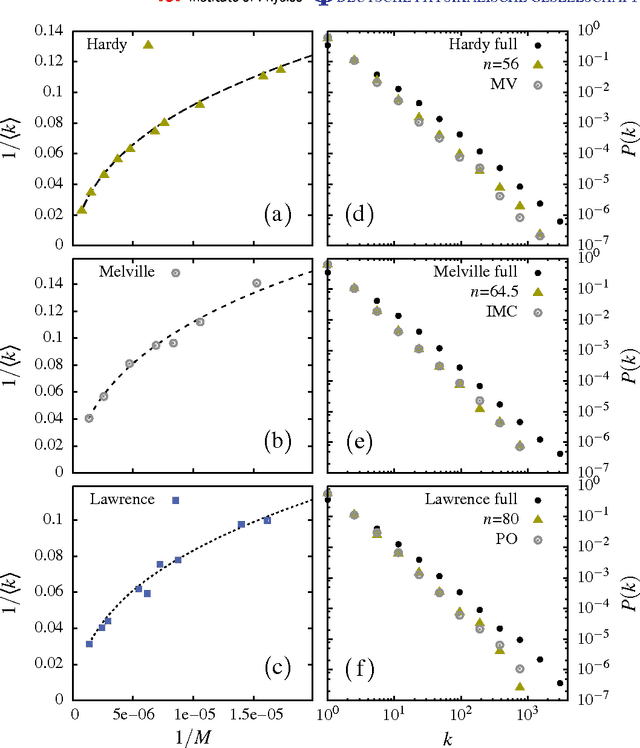
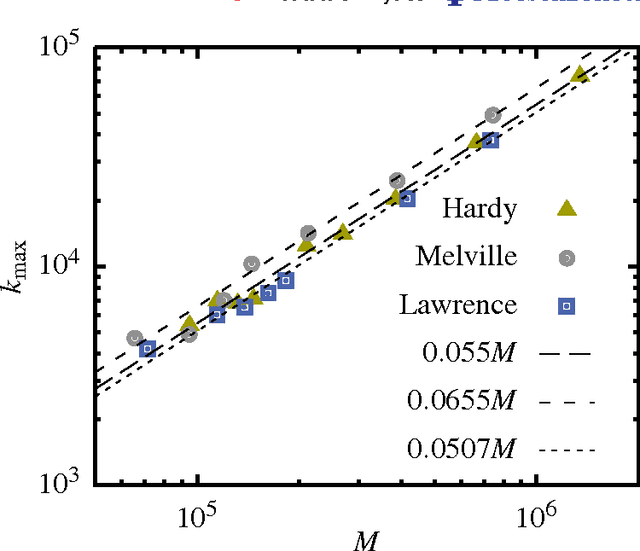
Evidence is given for a systematic text-length dependence of the power-law index gamma of a single book. The estimated gamma values are consistent with a monotonic decrease from 2 to 1 with increasing length of a text. A direct connection to an extended Heap's law is explored. The infinite book limit is, as a consequence, proposed to be given by gamma = 1 instead of the value gamma=2 expected if the Zipf's law was ubiquitously applicable. In addition we explore the idea that the systematic text-length dependence can be described by a meta book concept, which is an abstract representation reflecting the word-frequency structure of a text. According to this concept the word-frequency distribution of a text, with a certain length written by a single author, has the same characteristics as a text of the same length pulled out from an imaginary complete infinite corpus written by the same author.

Size dependent word frequencies and translational invariance of books

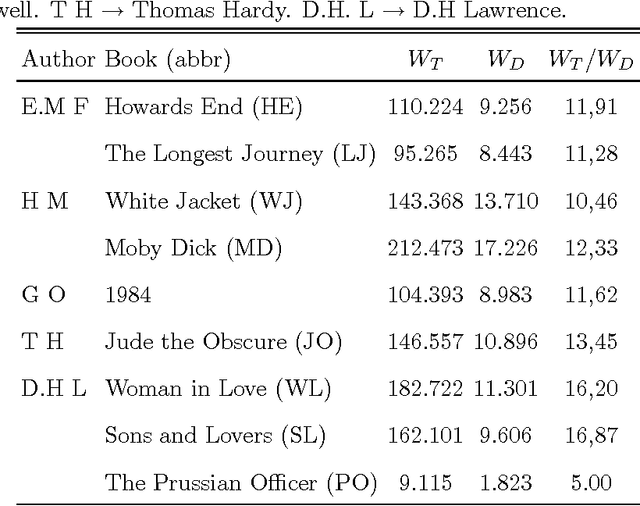
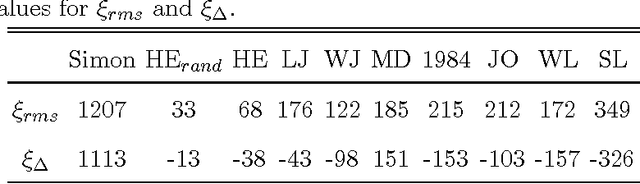
It is shown that a real novel shares many characteristic features with a null model in which the words are randomly distributed throughout the text. Such a common feature is a certain translational invariance of the text. Another is that the functional form of the word-frequency distribution of a novel depends on the length of the text in the same way as the null model. This means that an approximate power-law tail ascribed to the data will have an exponent which changes with the size of the text-section which is analyzed. A further consequence is that a novel cannot be described by text-evolution models like the Simon model. The size-transformation of a novel is found to be well described by a specific Random Book Transformation. This size transformation in addition enables a more precise determination of the functional form of the word-frequency distribution. The implications of the results are discussed.