The meta book and size-dependent properties of written language

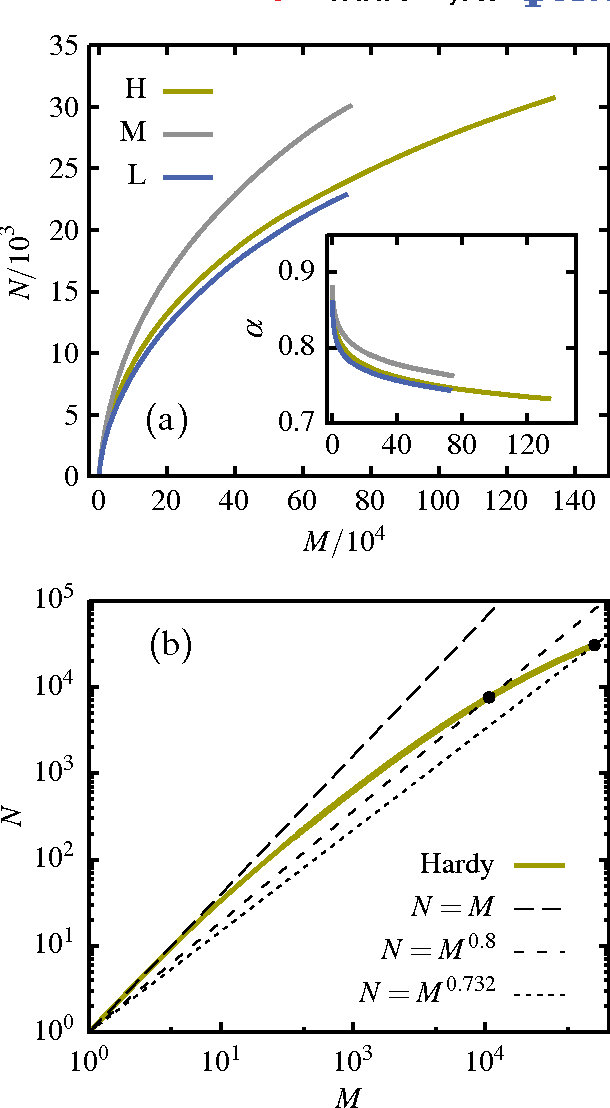
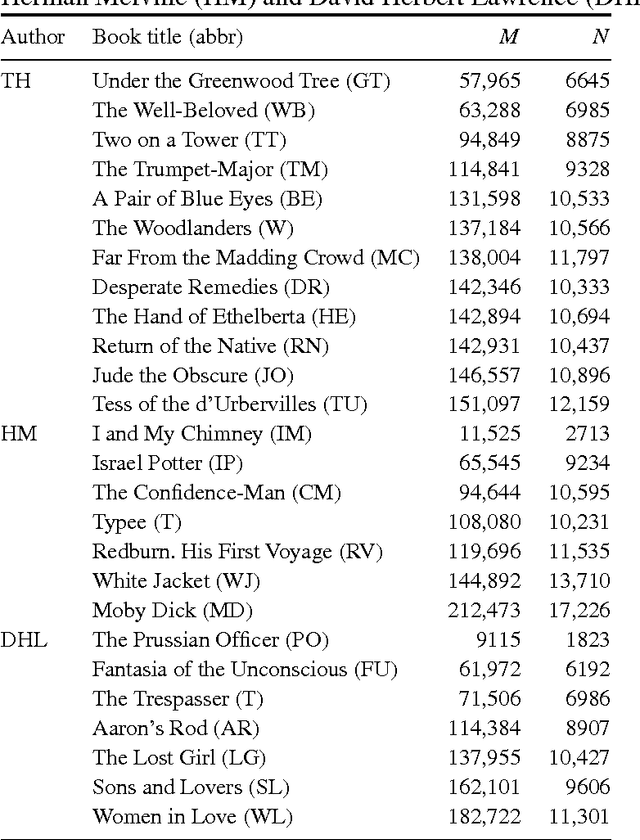
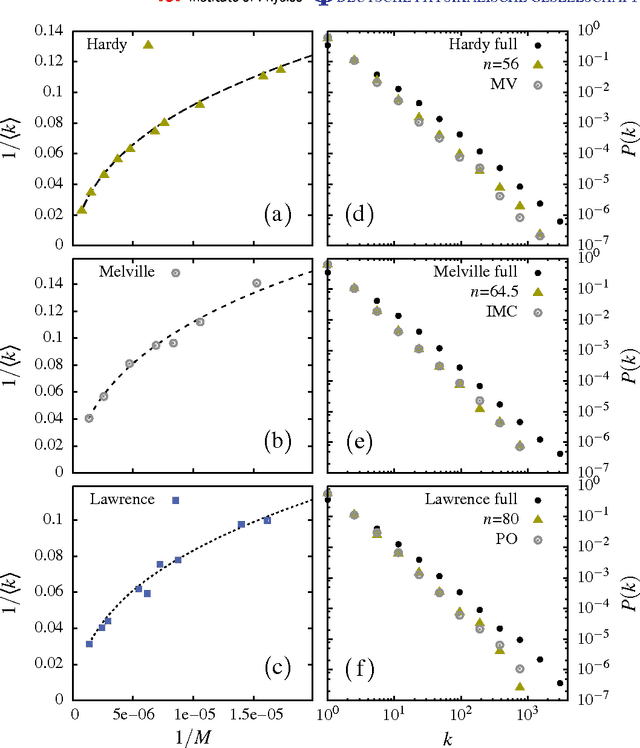
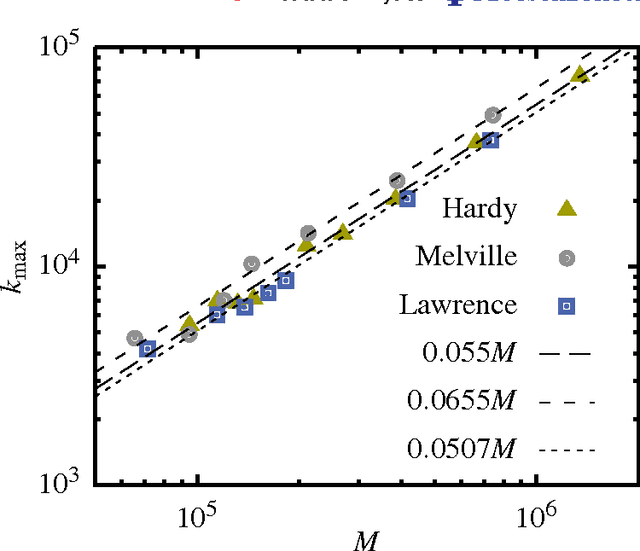
Evidence is given for a systematic text-length dependence of the power-law index gamma of a single book. The estimated gamma values are consistent with a monotonic decrease from 2 to 1 with increasing length of a text. A direct connection to an extended Heap's law is explored. The infinite book limit is, as a consequence, proposed to be given by gamma = 1 instead of the value gamma=2 expected if the Zipf's law was ubiquitously applicable. In addition we explore the idea that the systematic text-length dependence can be described by a meta book concept, which is an abstract representation reflecting the word-frequency structure of a text. According to this concept the word-frequency distribution of a text, with a certain length written by a single author, has the same characteristics as a text of the same length pulled out from an imaginary complete infinite corpus written by the same author.

Size dependent word frequencies and translational invariance of books

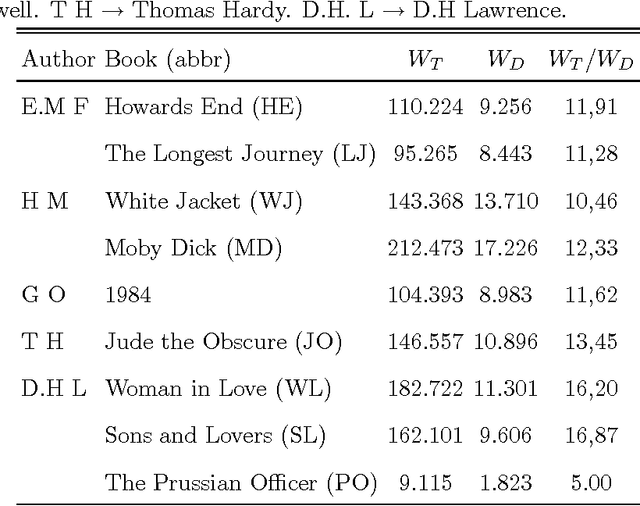
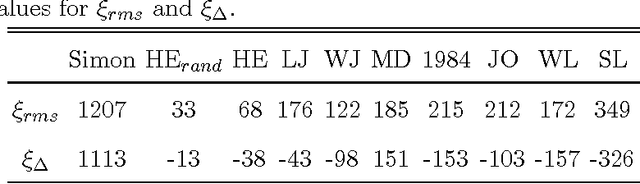
It is shown that a real novel shares many characteristic features with a null model in which the words are randomly distributed throughout the text. Such a common feature is a certain translational invariance of the text. Another is that the functional form of the word-frequency distribution of a novel depends on the length of the text in the same way as the null model. This means that an approximate power-law tail ascribed to the data will have an exponent which changes with the size of the text-section which is analyzed. A further consequence is that a novel cannot be described by text-evolution models like the Simon model. The size-transformation of a novel is found to be well described by a specific Random Book Transformation. This size transformation in addition enables a more precise determination of the functional form of the word-frequency distribution. The implications of the results are discussed.