The meta book and size-dependent properties of written language
Paper and Code
Sep 24, 2009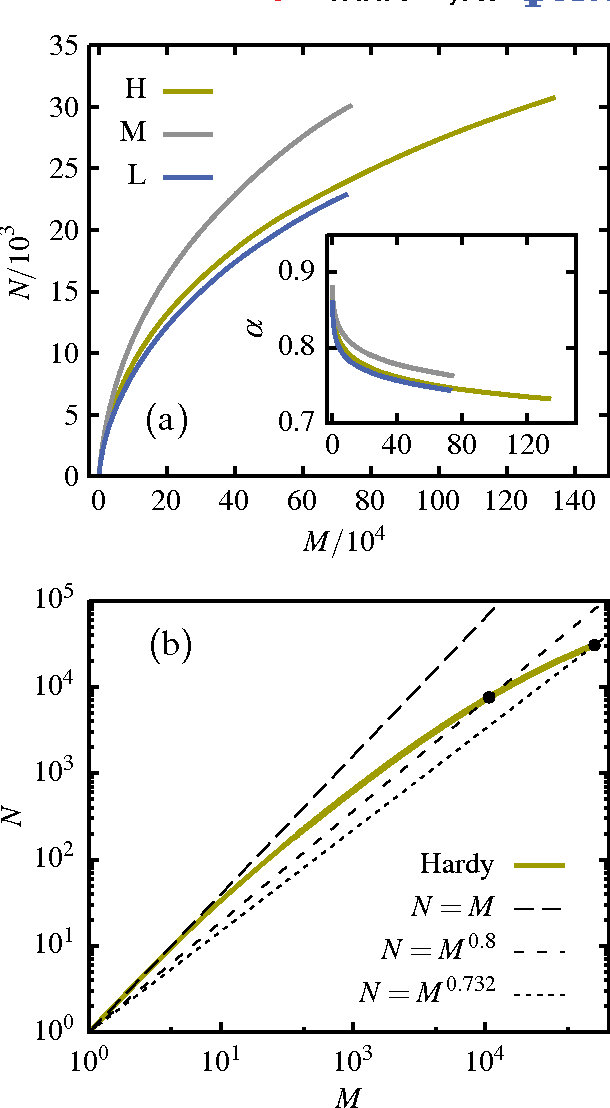
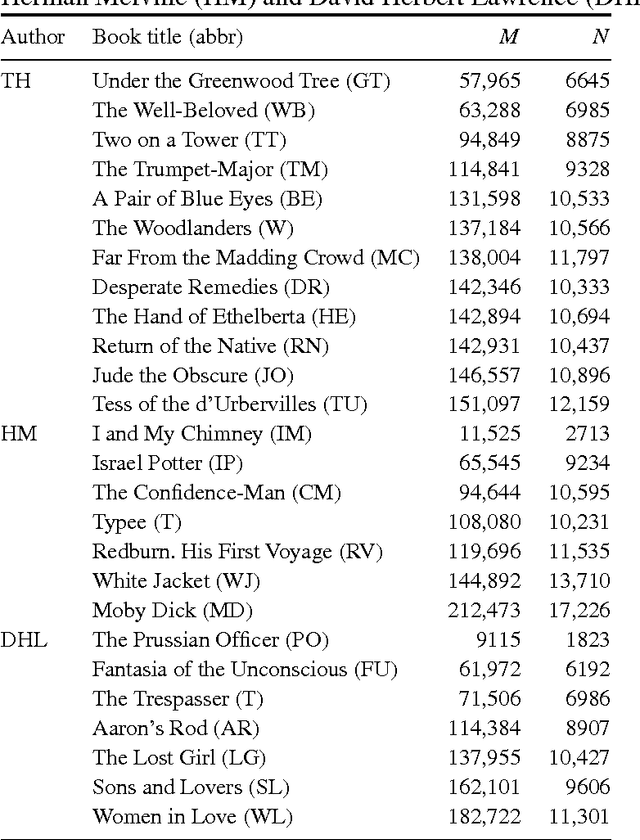
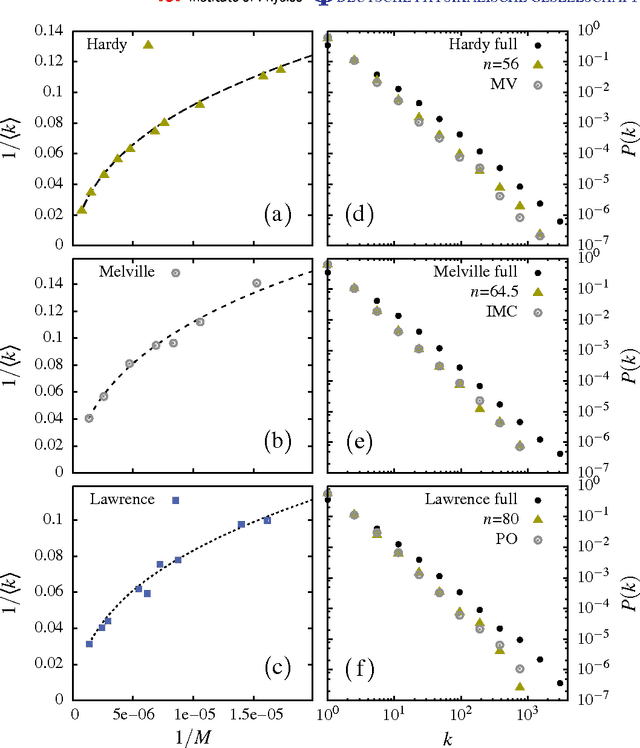
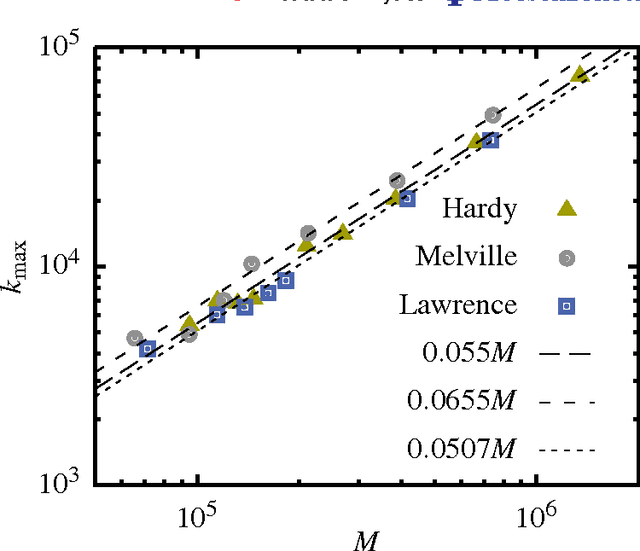
Evidence is given for a systematic text-length dependence of the power-law index gamma of a single book. The estimated gamma values are consistent with a monotonic decrease from 2 to 1 with increasing length of a text. A direct connection to an extended Heap's law is explored. The infinite book limit is, as a consequence, proposed to be given by gamma = 1 instead of the value gamma=2 expected if the Zipf's law was ubiquitously applicable. In addition we explore the idea that the systematic text-length dependence can be described by a meta book concept, which is an abstract representation reflecting the word-frequency structure of a text. According to this concept the word-frequency distribution of a text, with a certain length written by a single author, has the same characteristics as a text of the same length pulled out from an imaginary complete infinite corpus written by the same author.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge