Benford's Law and First Letter of Word

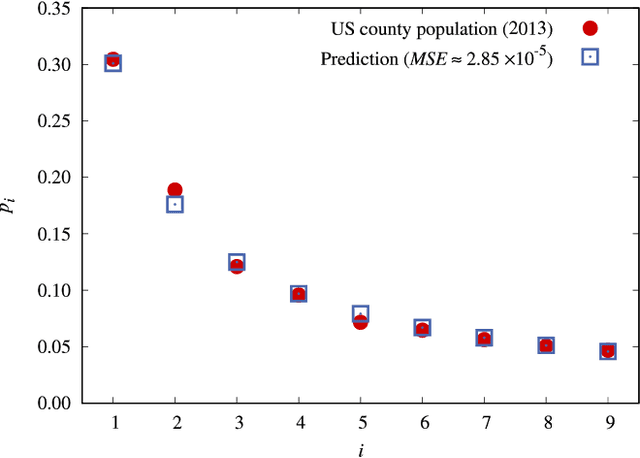
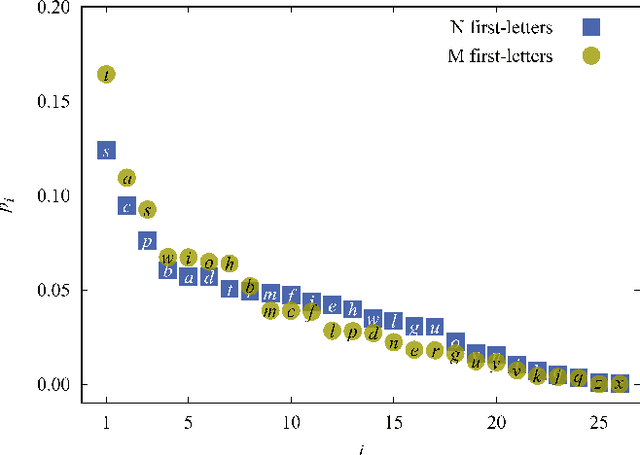
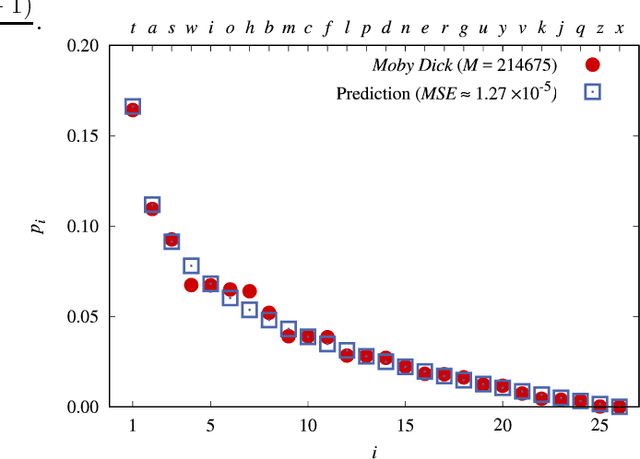
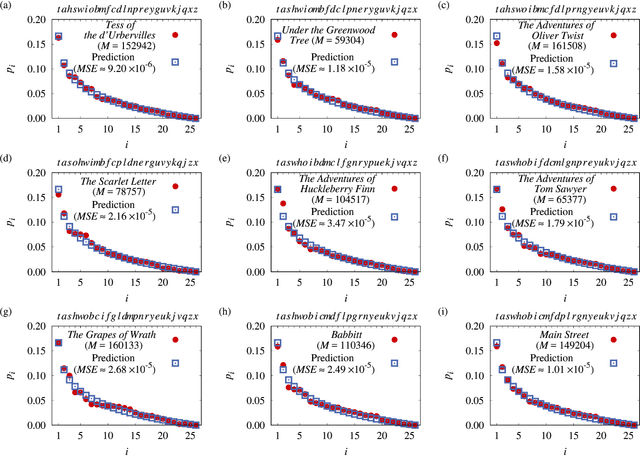
A universal First-Letter Law (FLL) is derived and described. It predicts the percentages of first letters for words in novels. The FLL is akin to Benford's law (BL) of first digits, which predicts the percentages of first digits in a data collection of numbers. Both are universal in the sense that FLL only depends on the numbers of letters in the alphabet, whereas BL only depends on the number of digits in the base of the number system. The existence of these types of universal laws appears counter-intuitive. Nonetheless both describe data very well. Relations to some earlier works are given. FLL predicts that an English author on the average starts about 16 out of 100 words with the English letter `t'. This is corroborated by data, yet an author can freely write anything. Fuller implications and the applicability of FLL remain for the future.

The Dependence of Frequency Distributions on Multiple Meanings of Words, Codes and Signs

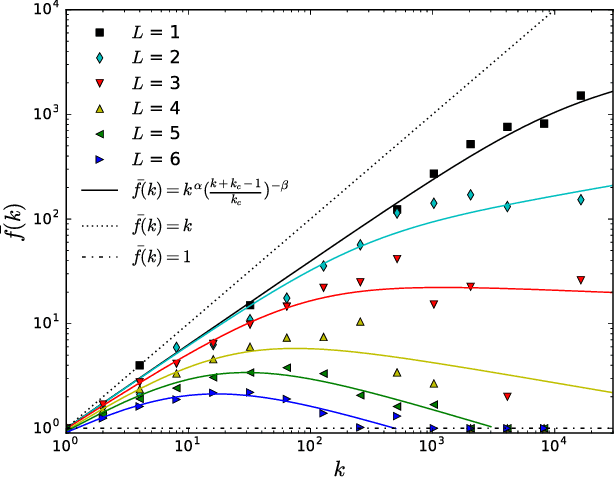
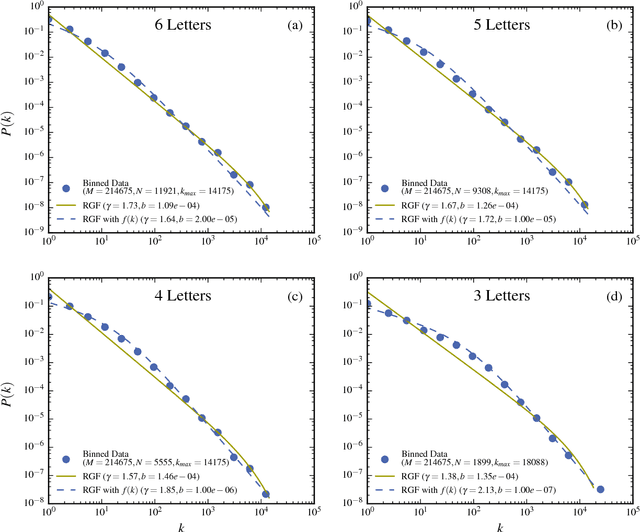
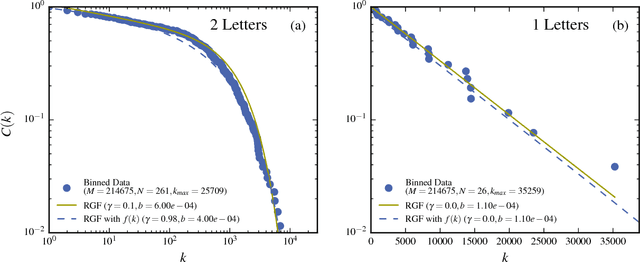
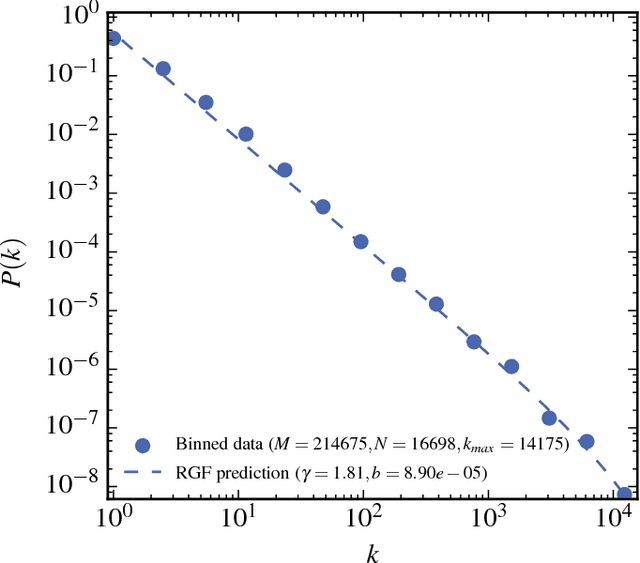
The dependence of the frequency distributions due to multiple meanings of words in a text is investigated by deleting letters. By coding the words with fewer letters the number of meanings per coded word increases. This increase is measured and used as an input in a predictive theory. For a text written in English, the word-frequency distribution is broad and fat-tailed, whereas if the words are only represented by their first letter the distribution becomes exponential. Both distribution are well predicted by the theory, as is the whole sequence obtained by consecutively representing the words by the first L=6,5,4,3,2,1 letters. Comparisons of texts written by Chinese characters and the same texts written by letter-codes are made and the similarity of the corresponding frequency-distributions are interpreted as a consequence of the multiple meanings of Chinese characters. This further implies that the difference of the shape for word-frequencies for an English text written by letters and a Chinese text written by Chinese characters is due to the coding and not to the language per se.