Power-grid stability predictions using transferable machine learning

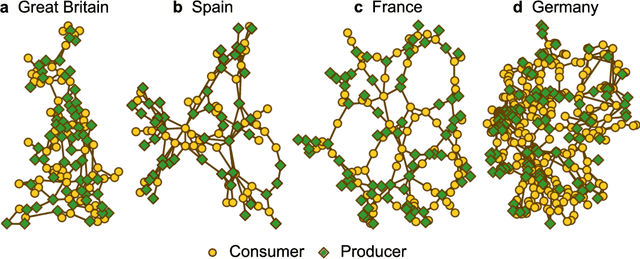
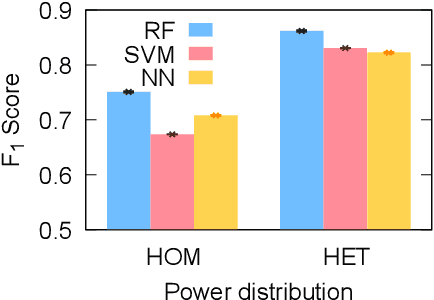
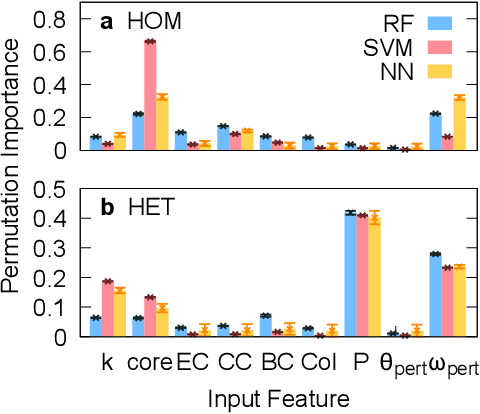
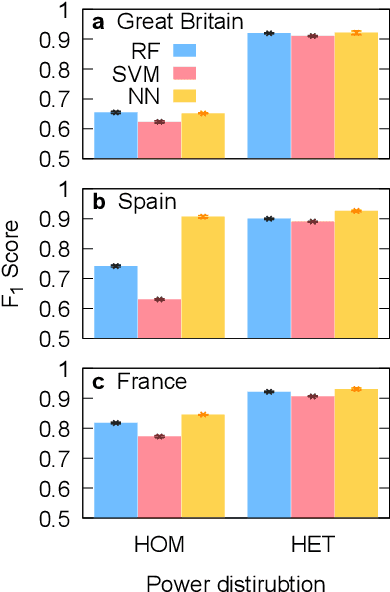
Complex network analyses have provided clues to improve power-grid stability with the help of numerical models. The high computational cost of numerical simulations, however, has inhibited the approach especially when it deals with the dynamic properties of power grids such as frequency synchronization. In this study, we investigate machine learning techniques to estimate the stability of power grid synchronization. We test three different machine learning algorithms -- random forest, support vector machine, and artificial neural network -- training them with two different types of synthetic power grids consisting of homogeneous and heterogeneous input-power distribution, respectively. We find that the three machine learning models better predict the synchronization stability of power-grid nodes when they are trained with the heterogeneous input-power distribution than the homogeneous one. With the real-world power grids of Great Britain, Spain, France, and Germany, we also demonstrate that the machine learning algorithms trained on synthetic power grids are transferable to the stability prediction of the real-world power grids, which implies the prospective applicability of machine learning techniques on power-grid studies.

Benford's Law and First Letter of Word

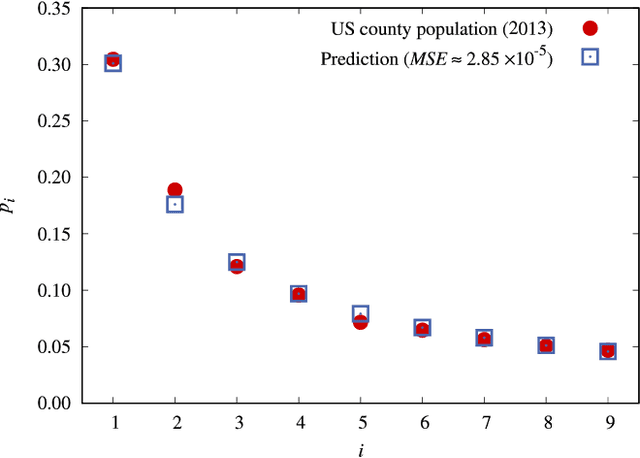
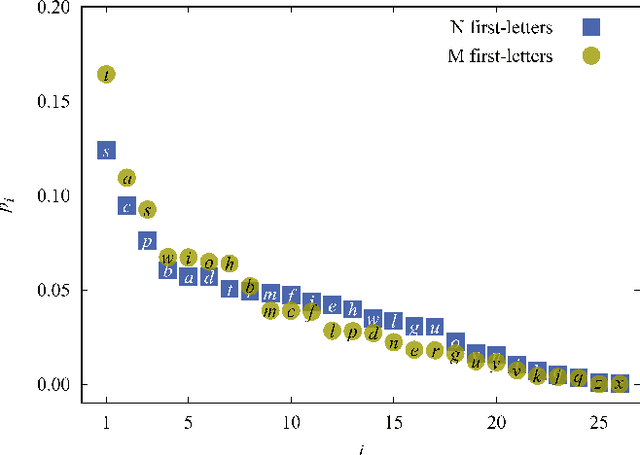
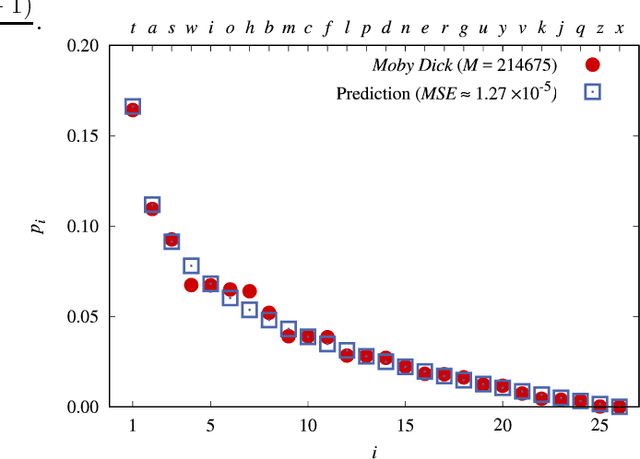
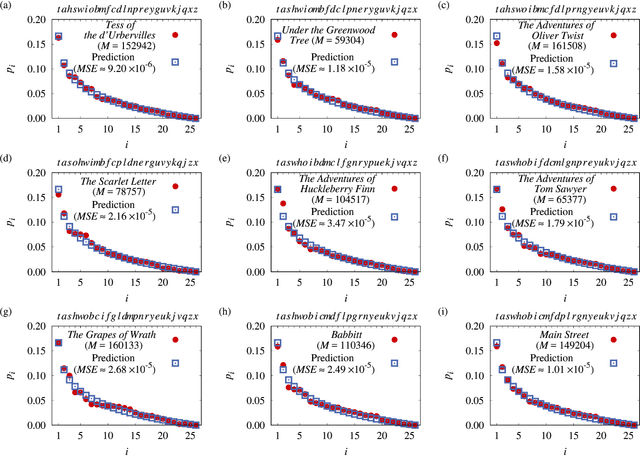
A universal First-Letter Law (FLL) is derived and described. It predicts the percentages of first letters for words in novels. The FLL is akin to Benford's law (BL) of first digits, which predicts the percentages of first digits in a data collection of numbers. Both are universal in the sense that FLL only depends on the numbers of letters in the alphabet, whereas BL only depends on the number of digits in the base of the number system. The existence of these types of universal laws appears counter-intuitive. Nonetheless both describe data very well. Relations to some earlier works are given. FLL predicts that an English author on the average starts about 16 out of 100 words with the English letter `t'. This is corroborated by data, yet an author can freely write anything. Fuller implications and the applicability of FLL remain for the future.