Benford's Law and First Letter of Word
Paper and Code
Dec 17, 2017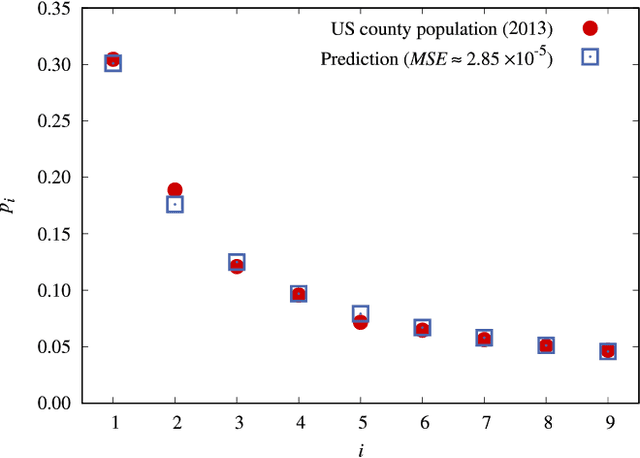
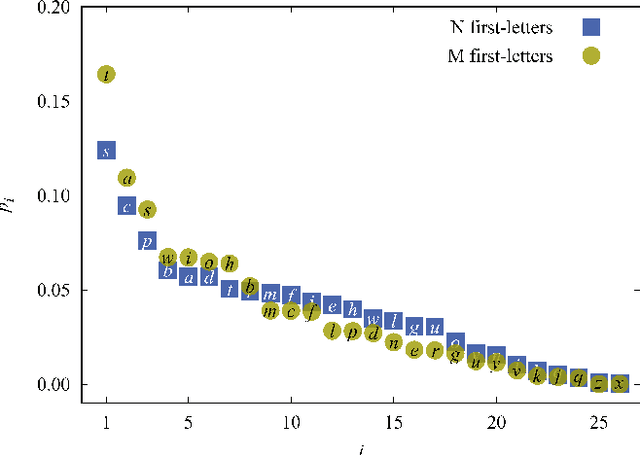
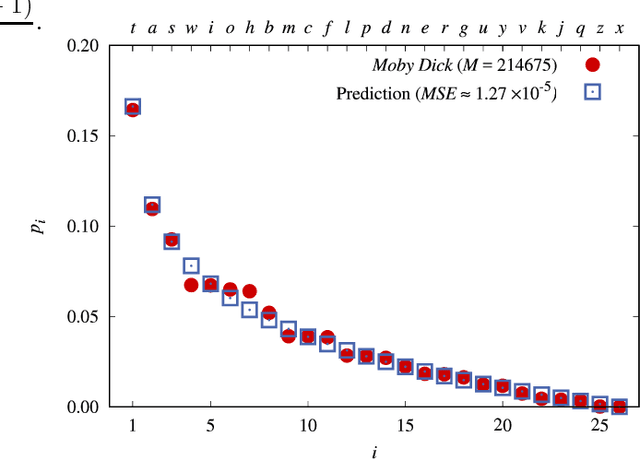
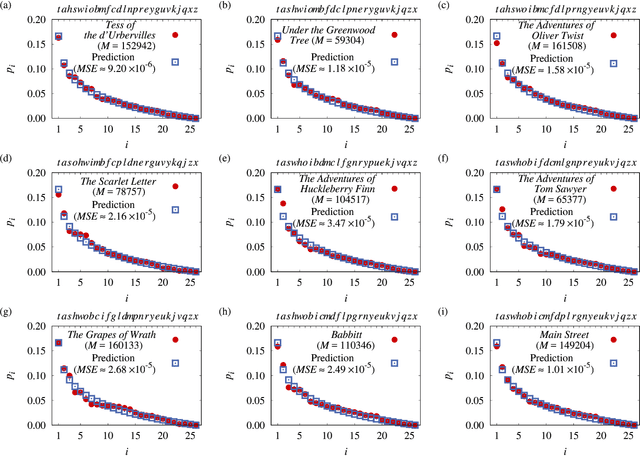
A universal First-Letter Law (FLL) is derived and described. It predicts the percentages of first letters for words in novels. The FLL is akin to Benford's law (BL) of first digits, which predicts the percentages of first digits in a data collection of numbers. Both are universal in the sense that FLL only depends on the numbers of letters in the alphabet, whereas BL only depends on the number of digits in the base of the number system. The existence of these types of universal laws appears counter-intuitive. Nonetheless both describe data very well. Relations to some earlier works are given. FLL predicts that an English author on the average starts about 16 out of 100 words with the English letter `t'. This is corroborated by data, yet an author can freely write anything. Fuller implications and the applicability of FLL remain for the future.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge