Generic Primitive Detection in Point Clouds Using Novel Minimal Quadric Fits

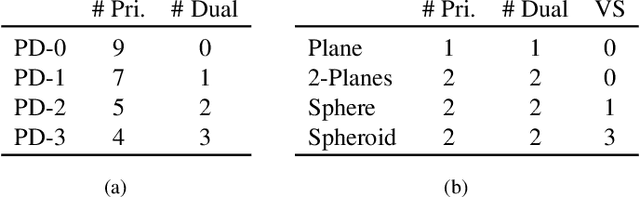
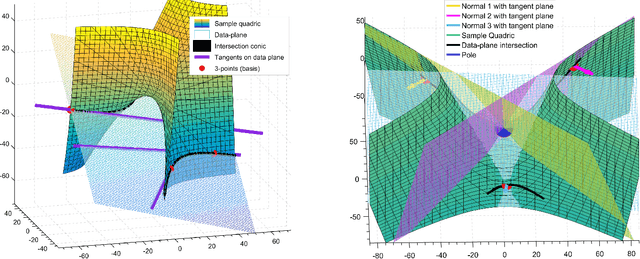
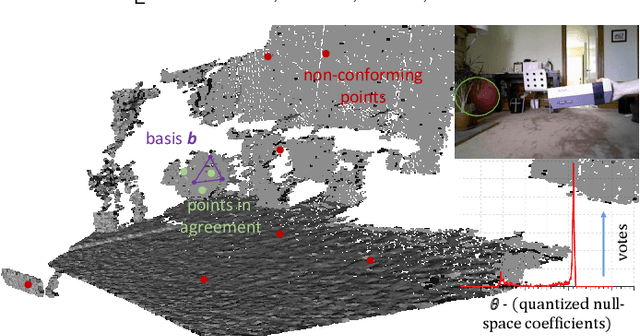
We present a novel and effective method for detecting 3D primitives in cluttered, unorganized point clouds, without axillary segmentation or type specification. We consider the quadric surfaces for encapsulating the basic building blocks of our environments - planes, spheres, ellipsoids, cones or cylinders, in a unified fashion. Moreover, quadrics allow us to model higher degree of freedom shapes, such as hyperboloids or paraboloids that could be used in non-rigid settings. We begin by contributing two novel quadric fits targeting 3D point sets that are endowed with tangent space information. Based upon the idea of aligning the quadric gradients with the surface normals, our first formulation is exact and requires as low as four oriented points. The second fit approximates the first, and reduces the computational effort. We theoretically analyze these fits with rigor, and give algebraic and geometric arguments. Next, by re-parameterizing the solution, we devise a new local Hough voting scheme on the null-space coefficients that is combined with RANSAC, reducing the complexity from $O(N^4)$ to $O(N^3)$ (three points). To the best of our knowledge, this is the first method capable of performing a generic cross-type multi-object primitive detection in difficult scenes without segmentation. Our extensive qualitative and quantitative results show that our method is efficient and flexible, as well as being accurate.

Calibration Wizard: A Guidance System for Camera Calibration

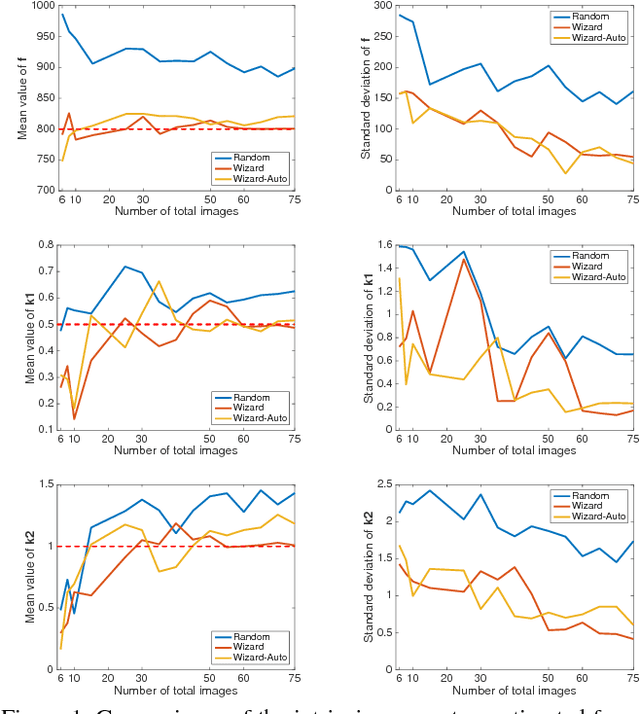
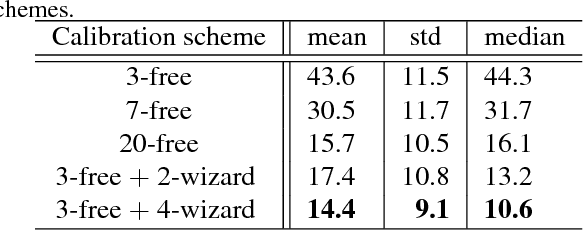
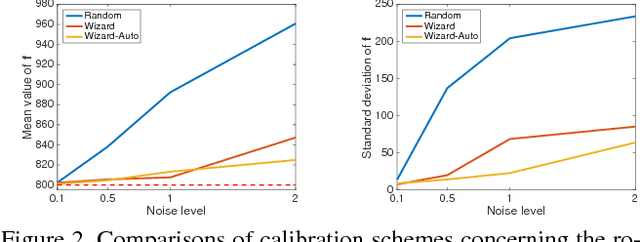
It is well known that the accuracy of a calibration depends strongly on the choice of camera poses from which images of a calibration object are acquired. We present a system -- Calibration Wizard -- that interactively guides a user towards taking optimal calibration images. For each new image to be taken, the system computes, from all previously acquired images, the pose that leads to the globally maximum reduction of expected uncertainty on intrinsic parameters and then guides the user towards that pose. We also show how to incorporate uncertainty in corner point position in a novel principled manner, for both, calibration and computation of the next best pose. Synthetic and real-world experiments are performed to demonstrate the effectiveness of Calibration Wizard.

A Minimalist Approach to Type-Agnostic Detection of Quadrics in Point Clouds

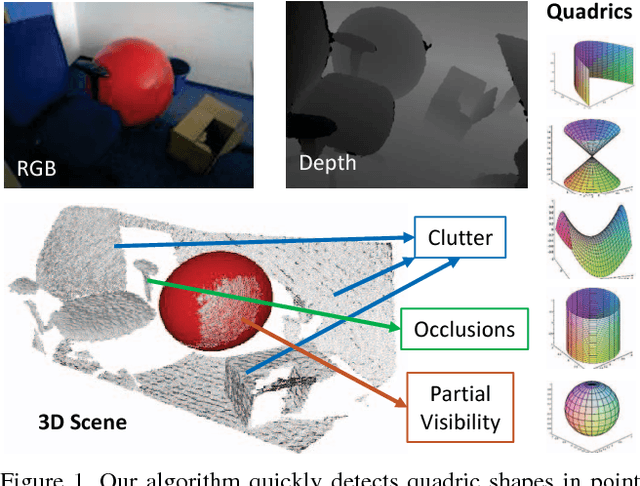
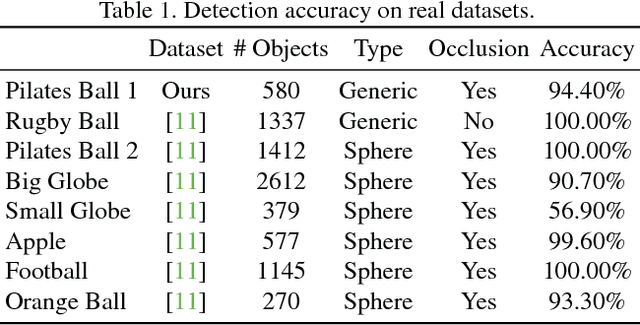
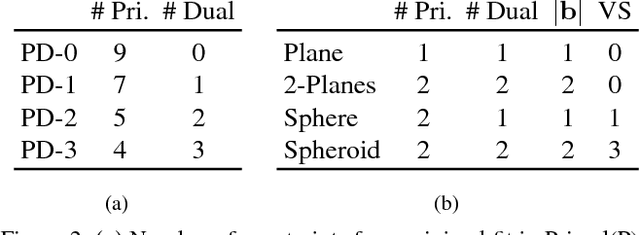
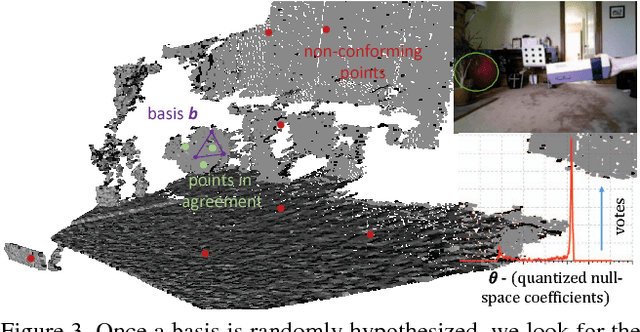
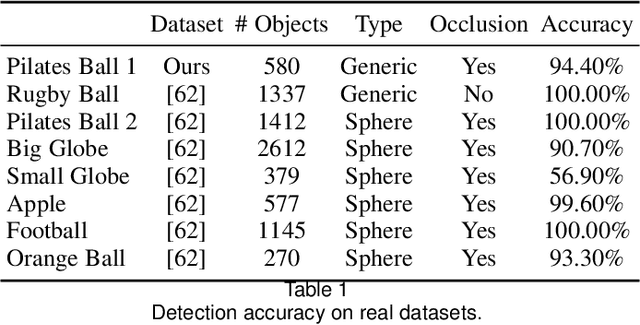
This paper proposes a segmentation-free, automatic and efficient procedure to detect general geometric quadric forms in point clouds, where clutter and occlusions are inevitable. Our everyday world is dominated by man-made objects which are designed using 3D primitives (such as planes, cones, spheres, cylinders, etc.). These objects are also omnipresent in industrial environments. This gives rise to the possibility of abstracting 3D scenes through primitives, thereby positions these geometric forms as an integral part of perception and high level 3D scene understanding. As opposed to state-of-the-art, where a tailored algorithm treats each primitive type separately, we propose to encapsulate all types in a single robust detection procedure. At the center of our approach lies a closed form 3D quadric fit, operating in both primal & dual spaces and requiring as low as 4 oriented-points. Around this fit, we design a novel, local null-space voting strategy to reduce the 4-point case to 3. Voting is coupled with the famous RANSAC and makes our algorithm orders of magnitude faster than its conventional counterparts. This is the first method capable of performing a generic cross-type multi-object primitive detection in difficult scenes. Results on synthetic and real datasets support the validity of our method.

Translation of "Zur Ermittlung eines Objektes aus zwei Perspektiven mit innerer Orientierung" by Erwin Kruppa (1913)

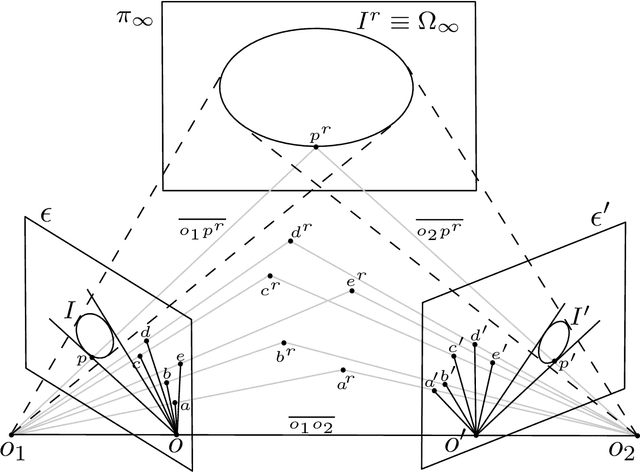
Erwin Kruppa's 1913 paper, Erwin Kruppa, "Zur Ermittlung eines Objektes aus zwei Perspektiven mit innerer Orientierung", Sitzungsberichte der Mathematisch-Naturwissenschaftlichen Kaiserlichen Akademie der Wissenschaften, Vol. 122 (1913), pp. 1939-1948, which may be translated as "To determine a 3D object from two perspective views with known inner orientation", is a landmark paper in Computer Vision because it provides the first five-point algorithm for relative pose estimation. Kruppa showed that (a finite number of solutions for) the relative pose between two calibrated images of a rigid object can be computed from five point matches between the images. Kruppa's work also gained attention in the topic of camera self-calibration, as presented in (Maybank and Faugeras, 1992). Since the paper is still relevant today (more than a hundred citations within the last ten years) and the paper is not available online, we ordered a copy from the German National Library in Frankfurt and provide an English translation along with the German original. We also adapt the terminology to a modern jargon and provide some clarifications (highlighted in sans-serif font). For a historical review of geometric computer vision, the reader is referred to the recent survey paper (Sturm, 2011).