A Minimalist Approach to Type-Agnostic Detection of Quadrics in Point Clouds
Paper and Code
Mar 19, 2018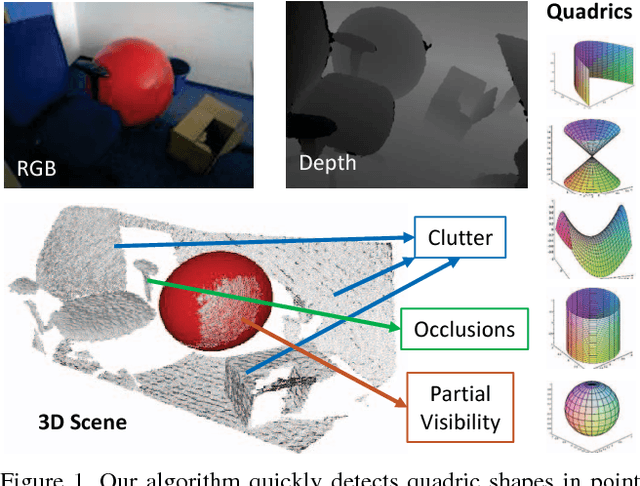
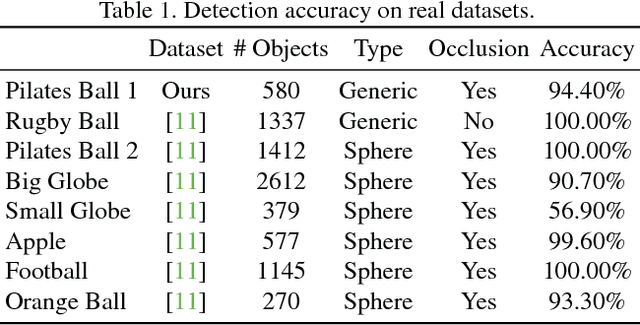
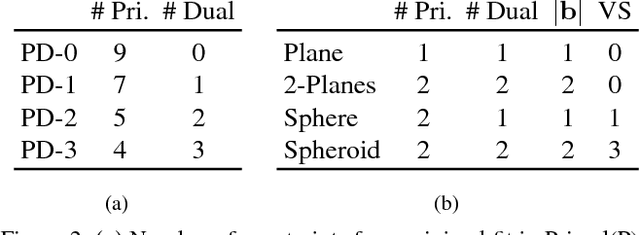
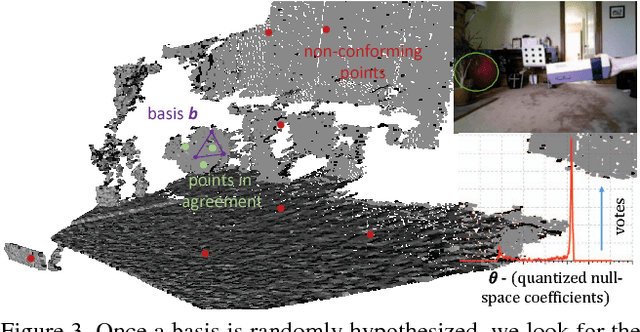
This paper proposes a segmentation-free, automatic and efficient procedure to detect general geometric quadric forms in point clouds, where clutter and occlusions are inevitable. Our everyday world is dominated by man-made objects which are designed using 3D primitives (such as planes, cones, spheres, cylinders, etc.). These objects are also omnipresent in industrial environments. This gives rise to the possibility of abstracting 3D scenes through primitives, thereby positions these geometric forms as an integral part of perception and high level 3D scene understanding. As opposed to state-of-the-art, where a tailored algorithm treats each primitive type separately, we propose to encapsulate all types in a single robust detection procedure. At the center of our approach lies a closed form 3D quadric fit, operating in both primal & dual spaces and requiring as low as 4 oriented-points. Around this fit, we design a novel, local null-space voting strategy to reduce the 4-point case to 3. Voting is coupled with the famous RANSAC and makes our algorithm orders of magnitude faster than its conventional counterparts. This is the first method capable of performing a generic cross-type multi-object primitive detection in difficult scenes. Results on synthetic and real datasets support the validity of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge