Splitting criteria for ordinal decision trees: an experimental study

Ordinal Classification (OC) is a machine learning field that addresses classification tasks where the labels exhibit a natural order. Unlike nominal classification, which treats all classes as equally distinct, OC takes the ordinal relationship into account, producing more accurate and relevant results. This is particularly critical in applications where the magnitude of classification errors has implications. Despite this, OC problems are often tackled using nominal methods, leading to suboptimal solutions. Although decision trees are one of the most popular classification approaches, ordinal tree-based approaches have received less attention when compared to other classifiers. This work conducts an experimental study of tree-based methodologies specifically designed to capture ordinal relationships. A comprehensive survey of ordinal splitting criteria is provided, standardising the notations used in the literature for clarity. Three ordinal splitting criteria, Ordinal Gini (OGini), Weighted Information Gain (WIG), and Ranking Impurity (RI), are compared to the nominal counterparts of the first two (Gini and information gain), by incorporating them into a decision tree classifier. An extensive repository considering 45 publicly available OC datasets is presented, supporting the first experimental comparison of ordinal and nominal splitting criteria using well-known OC evaluation metrics. Statistical analysis of the results highlights OGini as the most effective ordinal splitting criterion to date. Source code, datasets, and results are made available to the research community.

Improving the classification of extreme classes by means of loss regularisation and generalised beta distributions

An ordinal classification problem is one in which the target variable takes values on an ordinal scale. Nowadays, there are many of these problems associated with real-world tasks where it is crucial to accurately classify the extreme classes of the ordinal structure. In this work, we propose a unimodal regularisation approach that can be applied to any loss function to improve the classification performance of the first and last classes while maintaining good performance for the remainder. The proposed methodology is tested on six datasets with different numbers of classes, and compared with other unimodal regularisation methods in the literature. In addition, performance in the extreme classes is compared using a new metric that takes into account their sensitivities. Experimental results and statistical analysis show that the proposed methodology obtains a superior average performance considering different metrics. The results for the proposed metric show that the generalised beta distribution generally improves classification performance in the extreme classes. At the same time, the other five nominal and ordinal metrics considered show that the overall performance is aligned with the performance of previous alternatives.

Convolutional and Deep Learning based techniques for Time Series Ordinal Classification

Time Series Classification (TSC) covers the supervised learning problem where input data is provided in the form of series of values observed through repeated measurements over time, and whose objective is to predict the category to which they belong. When the class values are ordinal, classifiers that take this into account can perform better than nominal classifiers. Time Series Ordinal Classification (TSOC) is the field covering this gap, yet unexplored in the literature. There are a wide range of time series problems showing an ordered label structure, and TSC techniques that ignore the order relationship discard useful information. Hence, this paper presents a first benchmarking of TSOC methodologies, exploiting the ordering of the target labels to boost the performance of current TSC state-of-the-art. Both convolutional- and deep learning-based methodologies (among the best performing alternatives for nominal TSC) are adapted for TSOC. For the experiments, a selection of 18 ordinal problems from two well-known archives has been made. In this way, this paper contributes to the establishment of the state-of-the-art in TSOC. The results obtained by ordinal versions are found to be significantly better than current nominal TSC techniques in terms of ordinal performance metrics, outlining the importance of considering the ordering of the labels when dealing with this kind of problems.

A hybrid feature learning approach based on convolutional kernels for ATM fault prediction using event-log data

Predictive Maintenance (PdM) methods aim to facilitate the scheduling of maintenance work before equipment failure. In this context, detecting early faults in automated teller machines (ATMs) has become increasingly important since these machines are susceptible to various types of unpredictable failures. ATMs track execution status by generating massive event-log data that collect system messages unrelated to the failure event. Predicting machine failure based on event logs poses additional challenges, mainly in extracting features that might represent sequences of events indicating impending failures. Accordingly, feature learning approaches are currently being used in PdM, where informative features are learned automatically from minimally processed sensor data. However, a gap remains to be seen on how these approaches can be exploited for deriving relevant features from event-log-based data. To fill this gap, we present a predictive model based on a convolutional kernel (MiniROCKET and HYDRA) to extract features from the original event-log data and a linear classifier to classify the sample based on the learned features. The proposed methodology is applied to a significant real-world collected dataset. Experimental results demonstrated how one of the proposed convolutional kernels (i.e. HYDRA) exhibited the best classification performance (accuracy of 0.759 and AUC of 0.693). In addition, statistical analysis revealed that the HYDRA and MiniROCKET models significantly overcome one of the established state-of-the-art approaches in time series classification (InceptionTime), and three non-temporal ML methods from the literature. The predictive model was integrated into a container-based decision support system to support operators in the timely maintenance of ATMs.

A Dictionary-based approach to Time Series Ordinal Classification

Time Series Classification (TSC) is an extensively researched field from which a broad range of real-world problems can be addressed obtaining excellent results. One sort of the approaches performing well are the so-called dictionary-based techniques. The Temporal Dictionary Ensemble (TDE) is the current state-of-the-art dictionary-based TSC approach. In many TSC problems we find a natural ordering in the labels associated with the time series. This characteristic is referred to as ordinality, and can be exploited to improve the methods performance. The area dealing with ordinal time series is the Time Series Ordinal Classification (TSOC) field, which is yet unexplored. In this work, we present an ordinal adaptation of the TDE algorithm, known as ordinal TDE (O-TDE). For this, a comprehensive comparison using a set of 18 TSOC problems is performed. Experiments conducted show the improvement achieved by the ordinal dictionary-based approach in comparison to four other existing nominal dictionary-based techniques.

Monotonic classification: an overview on algorithms, performance measures and data sets

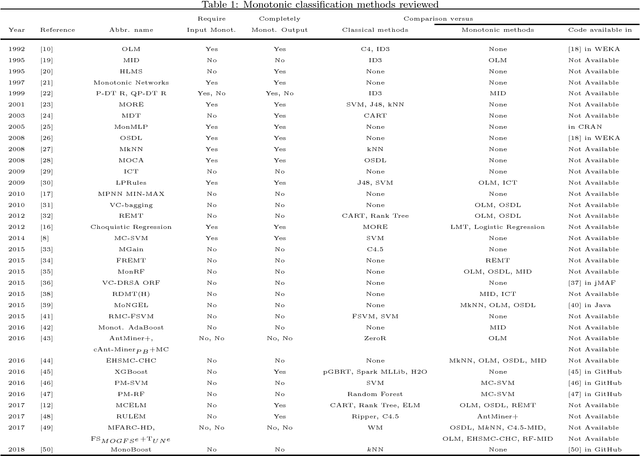
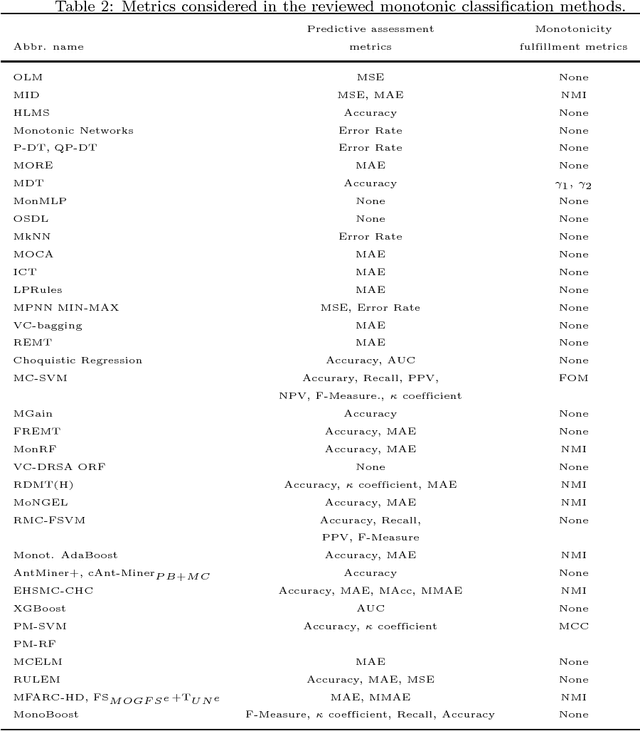
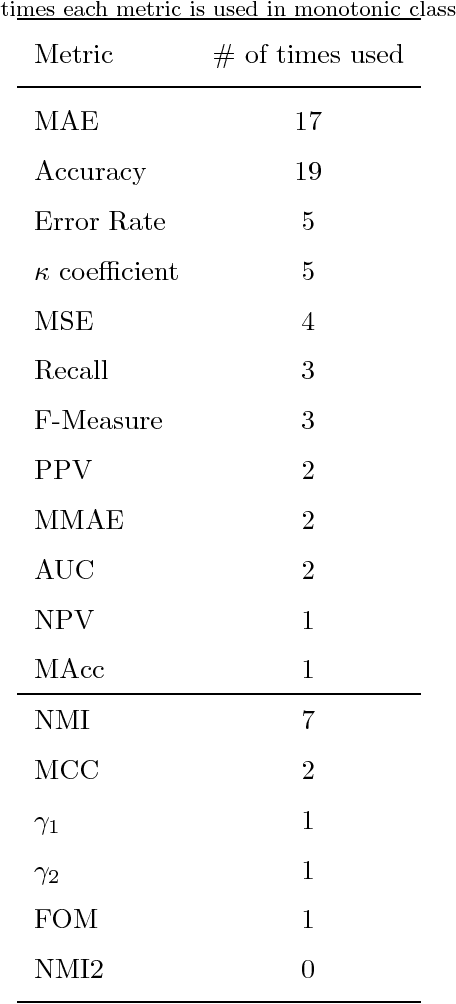
Currently, knowledge discovery in databases is an essential step to identify valid, novel and useful patterns for decision making. There are many real-world scenarios, such as bankruptcy prediction, option pricing or medical diagnosis, where the classification models to be learned need to fulfil restrictions of monotonicity (i.e. the target class label should not decrease when input attributes values increase). For instance, it is rational to assume that a higher debt ratio of a company should never result in a lower level of bankruptcy risk. Consequently, there is a growing interest from the data mining research community concerning monotonic predictive models. This paper aims to present an overview about the literature in the field, analyzing existing techniques and proposing a taxonomy of the algorithms based on the type of model generated. For each method, we review the quality metrics considered in the evaluation and the different data sets and monotonic problems used in the analysis. In this way, this paper serves as an overview of the research about monotonic classification in specialized literature and can be used as a functional guide of the field.

Time series clustering based on the characterisation of segment typologies

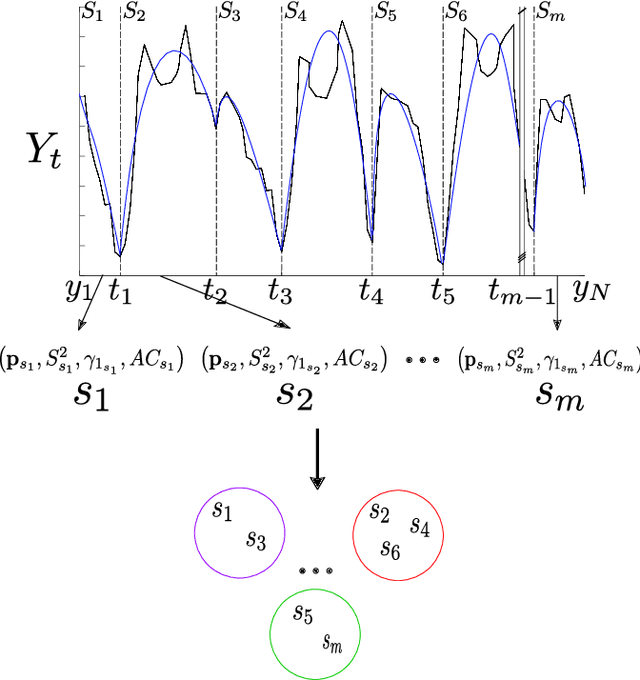
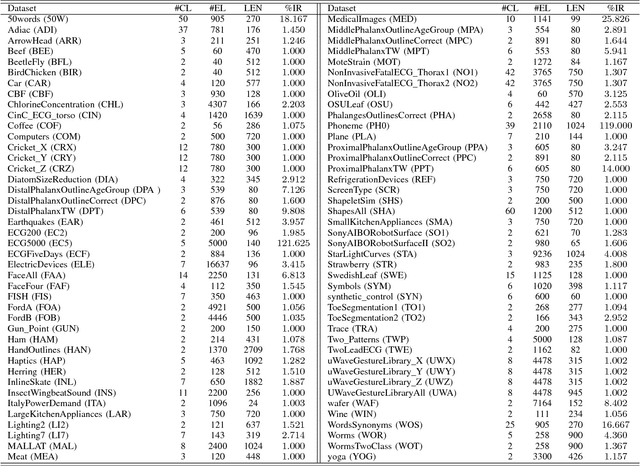
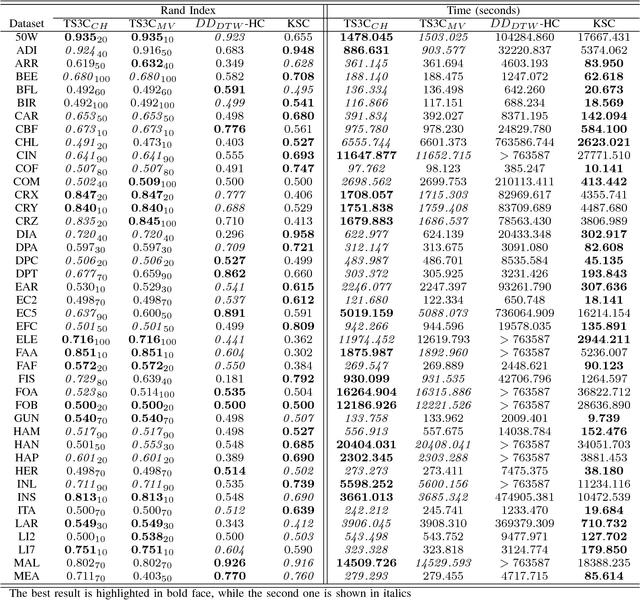
Time series clustering is the process of grouping time series with respect to their similarity or characteristics. Previous approaches usually combine a specific distance measure for time series and a standard clustering method. However, these approaches do not take the similarity of the different subsequences of each time series into account, which can be used to better compare the time series objects of the dataset. In this paper, we propose a novel technique of time series clustering based on two clustering stages. In a first step, a least squares polynomial segmentation procedure is applied to each time series, which is based on a growing window technique that returns different-length segments. Then, all the segments are projected into same dimensional space, based on the coefficients of the model that approximates the segment and a set of statistical features. After mapping, a first hierarchical clustering phase is applied to all mapped segments, returning groups of segments for each time series. These clusters are used to represent all time series in the same dimensional space, after defining another specific mapping process. In a second and final clustering stage, all the time series objects are grouped. We consider internal clustering quality to automatically adjust the main parameter of the algorithm, which is an error threshold for the segmenta- tion. The results obtained on 84 datasets from the UCR Time Series Classification Archive have been compared against two state-of-the-art methods, showing that the performance of this methodology is very promising.

OCAPIS: R package for Ordinal Classification And Preprocessing In Scala

Ordinal Data are those where a natural order exist between the labels. The classification and pre-processing of this type of data is attracting more and more interest in the area of machine learning, due to its presence in many common problems. Traditionally, ordinal classification problems have been approached as nominal problems. However, that implies not taking into account their natural order constraints. In this paper, an innovative R package named ocapis (Ordinal Classification and Preprocessing In Scala) is introduced. Implemented mainly in Scala and available through Github, this library includes four learners and two pre-processing algorithms for ordinal and monotonic data. Main features of the package and examples of installation and use are explained throughout this manuscript.